Enseignement Les épreuves du CRPE
Les repères
Imprimer
Dernier essai le - Score : /20
Abscisse
Sur une droite graduée, l'abscisse d'un point est le nombre qui permet de repérer la position de ce point sur la droite.
Dans un repère du plan, l'abscisse d'un point est l'un des deux nombres qui permet de repérer la position de ce point dans le repère. Elle se lit sur l'axe horizontal.
L'autre nombre est l'ordonnée. Abscisse et ordonnée sont les coordonnées d'un point : on cite toujours l'abscisse avant l'ordonnée.
Distance à zéro
Exemple
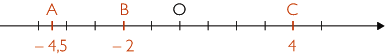La distance à zéro du nombre relatif   –4,5 est la longueur du segment [OA], c'est-à-dire 4,5. La distance à zéro du nombre relatif –2 est la longueur du segment [OB], c'est-à-dire 2. La distance à zéro du nombre relatif 4 est la longueur du segment [OC], c'est-à-dire 4.
Remarque
Deux nombres opposés (par exemple, –4 et 4) ont la même distance à zéro.
Droite graduée
Une droite graduée est une droite sur laquelle on a choisi :
  • un point auquel on associe le nombre 0 ; ce point est l'origine de la graduation ;
  • un segment unité que l'on reporte à partir du point origine pour graduer la droite ;
  • un sens positif.
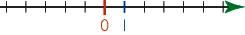Remarque
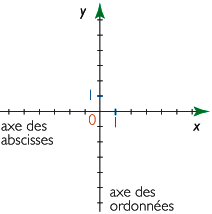
Un repère du plan est formé de deux droites graduées : l'axe des abscisses (axe horizontal) et l'axe des ordonnées (axe vertical).
Ordonnée
Dans un repère du plan, l'ordonnée d'un point est l'un des deux nombres qui permet de repérer la position de ce point dans le repère. Elle se lit sur l' axe vertical.
L'autre nombre est l'abscisse. Abscisse et ordonnée sont les coordonnées d'un point : on cite toujours l'abscisse avant l'ordonnée.
Origine d'un repère
L'origine d'une droite graduée, souvent notée O, est le point de la droite auquel on a choisi d'associer l' abscisse  0.
L'origine d'un repère du plan, souvent notée O, est le point d'intersection de l'axe des abscisses et de l'axe des ordonnées.
Il a pour coordonnées (0 ; 0).
Repère du plan
Un repère du plan est formé de deux axes, ayant la même origine.
Sur chacun de ces axes ont été définis un segment unité et un sens positif.
Remarque
Un repère orthogonal est formé de deux axes perpendiculaires. Dans un repère orthonormé (ou orthonormal), les deux axes sont perpendiculaires et l'unité sur chaque axe est représentée par des segments de même longueur.