Dernier essai le
- Score :
/20
Distance d'un point à une droite
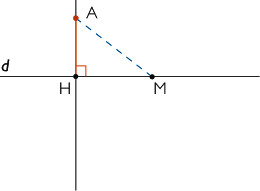 |
| Soit une droite d. Soit A un point et H le pied de la perpendiculaire à d passant par A. La longueur AH s'appelle la distance du point A à la droite d. |
Remarque
La distance AH est la plus petite distance entre A et un point de d. On voit sur la figure que, si M est un point de la droite distinct de H, alors AM > AH.
Distance entre deux points dans un repère du plan
Soit (O, I, J) un repère orthonormé du plan et A(x A ; y A), B(x B ; y B) deux points du plan.
La distance AB est donnée par la formule :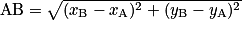 .
.
La distance AB est donnée par la formule :
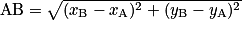 .
.Distance entre deux points sur une droite graduée
La distance entre deux points A et B est le plus court chemin pour aller de A à B. Elle est égale à la longueur du segment [AB].
Pour trouver la distance entre deux points A et B d'une droite graduée, on calcule la différence de leurs abscisses de la manière suivante : AB = BA = abscisse la plus grande – abscisse la plus petite, en se rappelant qu'une distance est toujours un nombre positif.
Exemple
La distance entre les points A et C est égale à 4 – (–4,5), soit 8,5. La distance entre les points A et B est égale à –2 – (–4,5), soit 2,5.
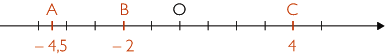 |
Parallèle
Deux droites qui, même indéfiniment prolongées, ne se coupent pas, sont parallèles.
Autrement dit : si deux droites n'ont aucun point commun, elles sont parallèles.
Soit deux droites parallèles D et D', on écrit : D // D'.
Autrement dit : si deux droites n'ont aucun point commun, elles sont parallèles.
Soit deux droites parallèles D et D', on écrit : D // D'.
Remarque
On peut dire également de deux segments qu'ils sont parallèles s'ils ont pour supports des droites parallèles.
Perpendiculaire
Deux droites sécantes qui forment un angle droit sont perpendiculaires (on peut dire également orthogonales).
Par un point donné, on ne peut mener qu'une seule perpendiculaire à une droite.
Par un point donné, on ne peut mener qu'une seule perpendiculaire à une droite.
Exemple
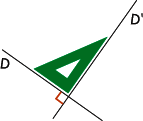 |
| | On écrit : 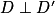 . . Les droites D et D' sont perpendiculaires. |
Remarque
On peut dire également de deux segments qu'ils sont perpendiculaires s'ils ont pour supports des droites perpendiculaires.
Document précédent
Les repères
Document suivant
La symétrie
