Enseignement Les épreuves du CRPE
La géométrie dans l'espace
Imprimer
Dernier essai le - Score : /20
Cône de révolution
Exemple
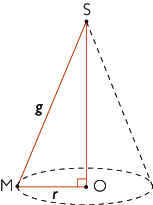Soit un triangle OSM rectangle en O. Le solide obtenu en faisant tourner le triangle autour d'un côté de l'angle droit, par exemple (OS), est un cône de révolution.

Observons le cône de révolution représenté ci-dessus en perspective. C'est un solide limité par :
  • une base qui a la forme d'un disque (ici, un disque de centre O et de rayon  r),
  • une surface latérale constituée de tous les segments joignant le point S aux points du bord du disque. Ces segments, appelés génératrices du cône, ont tous la même longueur  g.
Remarque
Le point S se trouve sur la perpendiculaire au disque passant par O. Le point S est le sommet du cône et le segment [SO], la hauteur du cône.
Cube (solide)
Un cube est un solide dont les 6 faces sont des carrés de mêmes dimensions.
C'est un parallélépipède rectangle particulier dont les trois dimensions sont égales.
Remarque
Un cube possède :
  • 6 faces carrées superposables,
  • 12 arêtes de même longueur,
  • 8 sommets.
Exemple
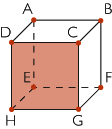Sur le cube représenté ci-dessus :
  • l'une des faces est DCGH,
  • [DC], [CG], [GF]… sont des arêtes,
  • les sommets sont A, B, C, D, E, F, G, H.
Polyèdre
Un polyèdre est un solide dont toutes les faces sont des polygones.
Exemple
Ces trois solides sont des polyèdres.
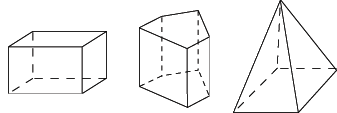pyramide ; prisme droit ; parallélépipède rectangle
Solide
Exemple
Le prisme droit, la pyramide, le cylindre, le cône, la sphère sont des solides (mais seuls le prisme droit et la pyramide sont des polyèdres).
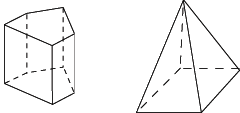pyramide ; prisme droit
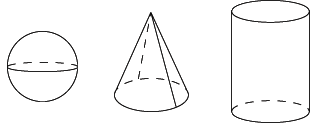sphère ; cône ; cylindre
En assemblant ces solides comme dans un jeu de construction, on obtient d'autres solides.
Remarque
Le prisme droit, la pyramide, le cylindre, le cône présentent des faces particulières appelées bases. La pyramide et le cône ont une seule base. Le prisme droit et le cylindre ont deux bases superposables.
Les autres faces de ces solides sont appelées faces latérales.
Sphère
Soit r un nombre positif ; l'ensemble des points de l'espace situés à la distance  r d'un point O constitue la sphère S de centre O et de rayon  r.
La boule   B, elle, est formée de l'ensemble des points dont la distance à O est inférieure ou égale à r, c'est-à-dire des points situés à l'intérieur de  S.
On appelle grand cercle de la sphère l'intersection d'une sphère avec un plan qui passe par son centre. Le rayon d'un grand cercle est égal au rayon de la sphère.
Exemple
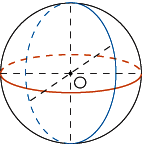Sur la figure ci-dessus, on a représenté une sphère et trois de ses grands cercles.