Dernier essai le
- Score :
/20
Ce sujet est composé de six exercices indépendants.
EXERCICE 1
Une directrice d'école primaire souhaite inscrire les élèves de l'école à une course solidaire d'Action contre la faim afin de les sensibiliser à la sous-nutrition dans le monde.
Il s'agit pour chaque élève de faire le plus de tours possible d'un parcours prédéfini. Pour chaque tour effectué, l'élève récolte une somme d'argent fixe qui sera versée à l'association caritative.
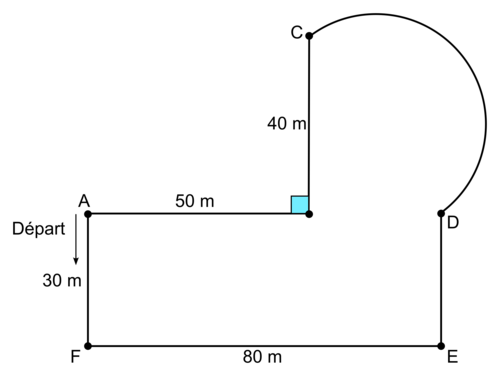
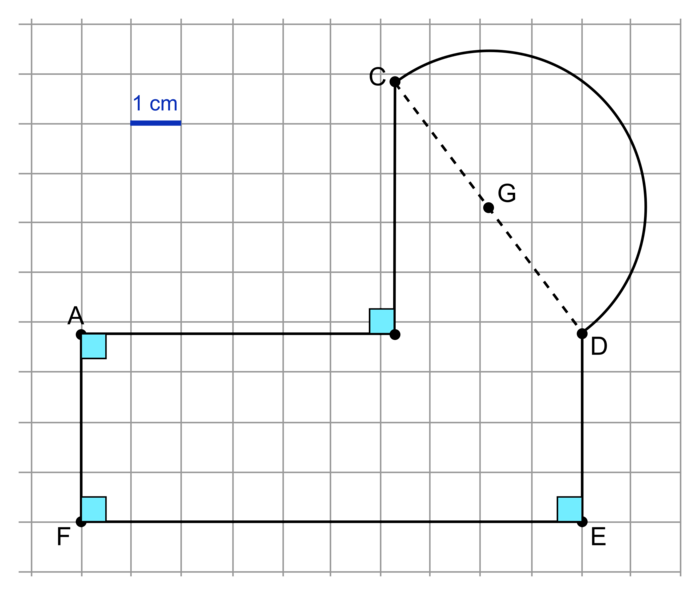
La directrice décide de faire courir les élèves dans la cour de l'école, le long d'un parcours schématisé ci-dessous. Une partie du parcours est constituée d'un demi-cercle de diamètre [CD] et les longueurs sont données en mètres.
Les points A, B, et D sont alignés et le quadrilatère AFED est un rectangle. Les élèves partent du point A et se déplacent dans le sens inverse des aiguilles d'une montre.
On a : AB = 50 m ; BC = 40 m ; EF = 80 m et FA = 30 m.
Il s'agit pour chaque élève de faire le plus de tours possible d'un parcours prédéfini. Pour chaque tour effectué, l'élève récolte une somme d'argent fixe qui sera versée à l'association caritative.
La directrice décide de faire courir les élèves dans la cour de l'école, le long d'un parcours schématisé ci-dessous. Une partie du parcours est constituée d'un demi-cercle de diamètre [CD] et les longueurs sont données en mètres.
Les points A, B, et D sont alignés et le quadrilatère AFED est un rectangle. Les élèves partent du point A et se déplacent dans le sens inverse des aiguilles d'une montre.
On a : AB = 50 m ; BC = 40 m ; EF = 80 m et FA = 30 m.
 |
1. Calculer la longueur du segment [CD].
2. Montrer que la longueur du parcours, arrondie au mètre, est 309 m.
On utilisera cette valeur dans la suite de l'exercice.
On utilisera cette valeur dans la suite de l'exercice.
3. Construire un plan du parcours à l'échelle 1/800.
4. Killian a effectué un tour complet en 3 minutes.
À quelle vitesse moyenne Killian a-t-il couru ? On donnera le résultat en mètres par seconde, arrondi au centième, puis en kilomètres par heure, arrondi au dixième.
À quelle vitesse moyenne Killian a-t-il couru ? On donnera le résultat en mètres par seconde, arrondi au centième, puis en kilomètres par heure, arrondi au dixième.
5.
On suppose que Sophia court à une vitesse constante de 7 km/h.
a. Combien de tours complets pourrait-elle effectuer à cette vitesse en 18 minutes ?
b. On désigne par S le point du parcours où Sophia se trouve au bout de 18 minutes de course. Placer le point S sur le plan réalisé à la question 3.
6.
L'école est composée de 325 élèves. Le tableau ci-dessous indique le nombre de tours complets effectués par les élèves.
| Nombre de tours | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nombre d'élèves | 52 | 52 | 78 | 65 | 39 | 26 | 13 |
a. Quel est le nombre moyen de tours complets effectués ?
b. Quelle est l'étendue de cette série statistique ?
c. Déterminer la médiane de cette série statistique.
d. Interpréter le résultat de la question c.
e. Déterminer le premier et le troisième quartile de cette série.
f. Quel pourcentage d'élèves ont réussi à faire au moins 4 tours ?
EXERCICE 2
Un rectangle est défini dans le dictionnaire de la façon suivante :
« Un rectangle est un quadrilatère dont les quatre angles sont droits. »
« Un rectangle est un quadrilatère dont les quatre angles sont droits. »
1. Un quadrilatère qui possède deux angles droits est-il un rectangle ? Justifier.
2.
Dans une classe de CE2, une enseignante demande à ses élèves de compléter la phrase suivante : « Un rectangle est un quadrilatère dont… »
Voici deux réponses proposées :
Élève A : « Un rectangle est un quadrilatère dont les côtés opposés sont de même longueur. »
Élève B : « Un rectangle est un quadrilatère dont les diagonales sont de même longueur. »
Voici deux réponses proposées :
Élève A : « Un rectangle est un quadrilatère dont les côtés opposés sont de même longueur. »
Élève B : « Un rectangle est un quadrilatère dont les diagonales sont de même longueur. »
a. Préciser en quoi la réponse de l'élève A ne pourrait pas être admise comme définition mathématique du rectangle.
b. Préciser en quoi la réponse de l'élève B ne pourrait pas être admise comme définition mathématique du rectangle.
3. Quelle est la nature d'un rectangle dont les diagonales sont perpendiculaires ?
4.
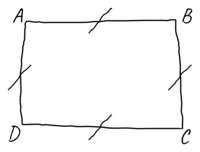
En s'appuyant sur le codage du quadrilatère ci-après dessiné à main levée, préciser la nature du quadrilatère en question en justifiant la réponse.
 |
EXERCICE 3
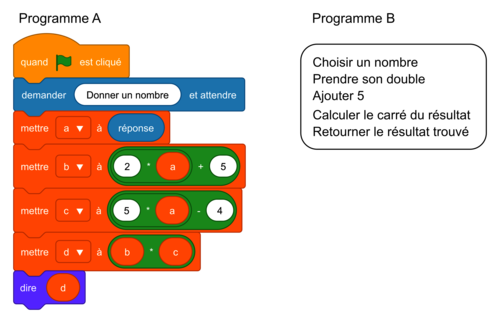
Voici deux programmes de calcul :
Programme A
Programme A
 |
Programme B
| Choisir un nombre Prendre son double Ajouter 5 Calculer le carré du résultat Retourner le résultat trouvé |
1. Montrer que si l'utilisateur saisit le nombre 2, alors le programme A retourne le nombre 54.
2. Calculer le résultat obtenu avec le programme A si le nombre saisi par l'utilisateur est 1,15.
3. Pour quel(s) nombre(s) de départ le programme A retourne-t-il le nombre 0 ?
4.
a. Si l'utilisateur saisit le nombre 3, quel résultat le programme B retourne-t-il ?
b. Si l'utilisateur saisit le nombre 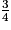 , quel résultat le programme B retourne-t-il ?
, quel résultat le programme B retourne-t-il ?
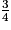 , quel résultat le programme B retourne-t-il ?
, quel résultat le programme B retourne-t-il ?5.
On détermine les résultats suivants retournés par le programme B à l'aide d'une feuille de calcul automatisé.
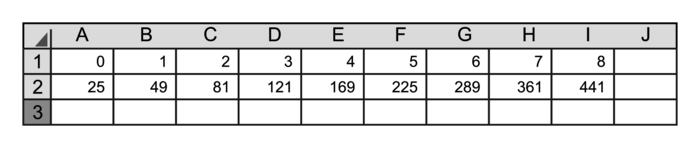 |
a. Quelle cellule du tableur permet de retrouver la réponse à la question 4.a. ci-dessus ?
b. Quelle formule a pu être saisie dans la cellule A2 de la feuille de calcul automatisé afin de la copier-glisser sur la ligne 2 ?
6.
a. Pour quel nombre de départ le programme B retourne-t-il le nombre 0 ?
b. Ce nombre de départ est-il rationnel ? Justifier.
c. Ce nombre de départ est-il décimal ? Justifier.
7. Pour quel(s) nombre(s) de départ le programme A retourne-t-il le même résultat que le programme B ?
EXERCICE 4
Deux élèves de CM2, Jeanne et Teddy, jouent à la bataille navale. Il s'agit d'un jeu de société, appelé également « touché-coulé ».
Les deux joueurs doivent commencer par placer quatre navires horizontalement ou verticalement (sans chevauchement) sur leur grille de 8 lignes et 8 colonnes, tenue secrète : 1 navire de deux cases, 2 navires de trois cases et 1 navire de quatre cases.
Ils doivent ensuite tenter de faire « couler » les navires adverses en « touchant » toutes les cases de chaque navire de l'autre joueur. Pour cela, chacun, à son tour, énonce une case de la grille, sous le format « lettre-nombre », par exemple C2.
Lorsqu'un joueur énonce une case, son adversaire répond :
Voici ci-dessous la grille de Teddy : les quatre bateaux sont schématisés par des rectangles gris.
On suppose qu'à chaque tir, Jeanne choisit au hasard et de manière équiprobable une case de la grille qu'elle n'a pas énoncée précédemment.
Les deux joueurs doivent commencer par placer quatre navires horizontalement ou verticalement (sans chevauchement) sur leur grille de 8 lignes et 8 colonnes, tenue secrète : 1 navire de deux cases, 2 navires de trois cases et 1 navire de quatre cases.
Ils doivent ensuite tenter de faire « couler » les navires adverses en « touchant » toutes les cases de chaque navire de l'autre joueur. Pour cela, chacun, à son tour, énonce une case de la grille, sous le format « lettre-nombre », par exemple C2.
Lorsqu'un joueur énonce une case, son adversaire répond :
- « À l'eau ! » si la case énoncée est vide ;
- « Touché ! » si la case énoncée est occupée par un morceau de navire et si les autres parties du navire n'ont pas encore toutes été touchées ;
- « Touché-coulé ! » si la case énoncée est occupée par un morceau de navire et si toutes les autres parties du navire ont déjà été touchées.
Voici ci-dessous la grille de Teddy : les quatre bateaux sont schématisés par des rectangles gris.
On suppose qu'à chaque tir, Jeanne choisit au hasard et de manière équiprobable une case de la grille qu'elle n'a pas énoncée précédemment.
 |
1.
Au premier essai :
a. Quelle est la probabilité que Jeanne touche un bateau ?
b. Quelle est la probabilité que Jeanne ne touche aucun bateau ?
c. Un des bateaux a une chance sur seize d'être touché. De combien de cases est-il composé ?
d. Jeanne choisit une case de la colonne B. Quelle est la probabilité qu'elle touche un bateau ?
2. Au premier essai de la partie, Jeanne désigne la case « E1 ». Teddy annonce « Touché ! ». Jeanne souhaite couler le bateau touché et choisit une case adjacente à la case « E1 ». Quelle est la probabilité qu'elle coule le bateau au coup suivant ? Justifier.
3. Teddy annonce « À l'eau ! » pour les deux premiers essais de Jeanne. Quelle est la probabilité de toucher un bateau pour son troisième essai ?
EXERCICE 5
Pour choisir une unité de température, les physiciens se sont heurtés à l'absence de « température zéro » (le zéro absolu n'était pas connu à l'époque). Deux systèmes principaux ont été créés et restent utilisés : le degré Celsius (°C) et le degré Fahrenheit (°F).
Voici ci-dessous une formule permettant de passer de la mesure d'une température en degrés Fahrenheit (notée F) vers la mesure de la même température en degrés Celsius (notée C).
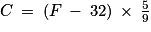
Voici ci-dessous une formule permettant de passer de la mesure d'une température en degrés Fahrenheit (notée F) vers la mesure de la même température en degrés Celsius (notée C).
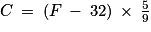
1. En utilisant cette formule, convertir 95 °F en degrés Celsius.
2. En utilisant cette formule, convertir 5 °C en degrés Fahrenheit.
3. Existe-t-il des températures pour lesquelles la mesure en degrés Celsius est égale à la mesure en degrés Fahrenheit ? Donner toutes les réponse possibles en justifiant.
EXERCICE 6
Un professeur des écoles d'une classe de CE1 présente à ses élèves une règle de calcul qui permet de déterminer avec ses dix doigts et ses dix orteils le produit de deux nombres entiers compris entre 5 et 10 en utilisant les résultats des tables appris précédemment. Il s'appuie sur l'exemple suivant :
Effectuons 6 × 7.
Effectuons 6 × 7.
- Avec le pied et la main gauches, on lève les 5 orteils et 1 doigt, représentant ainsi le 6.
- Avec le pied et la main droits, on lève les 5 orteils et 2 doigts, représentant ainsi le 7. Pour le calcul, on ne regarde que les mains et on procède de la manière suivante : la somme du nombre de doigts levés nous indique un nombre de dizaines, le produit des doigts baissés nous indique un nombre d'unités. Ici on a : (1 + 2) dizaines et (4 × 3) unités, soit encore 3 dizaines et 12 unités. On obtient donc le nombre 42.
1. Appliquer cette règle pour calculer le produit 6 × 8.
2.
On note g le nombre de doigts levés de la main gauche et d le nombre de doigts levés de la main droite.
a. Que représentent dans ce contexte les nombres (5 − g) et (5 − d) ?
b. Démontrer l'égalité : (5 + g)(5 + d) = 10(g + d) + (5 − g)(5 − d).
c. Conclure quant à la validité de la règle de calcul.
Corrigé
Corrigé
Exercice 1
1.
Puisque AFED est un rectangle, ses côtés opposés [FE] et [AD] sont de même longueur.
Puisque les points A, B et D sont alignés dans cet ordre, B est un point de [AD]. Donc :
BD = AD − AB = FE − AB = 80 m − 50 m = 30 m.
Puisque les points A, B et D sont alignés, les droites (AB) et (BD) sont confondues.
La droite (CB) est codée comme étant perpendiculaire à la droite (AB) donc à la droite (BD) ; le triangle BCD est donc rectangle en B.
Puisque les points A, B et D sont alignés dans cet ordre, B est un point de [AD]. Donc :
BD = AD − AB = FE − AB = 80 m − 50 m = 30 m.
Puisque les points A, B et D sont alignés, les droites (AB) et (BD) sont confondues.
La droite (CB) est codée comme étant perpendiculaire à la droite (AB) donc à la droite (BD) ; le triangle BCD est donc rectangle en B.
Propriété de Pythagore (permettant de calculer la longueur d'un côté d'un triangle rectangle quand on connaît la longueur de ses deux autres côtés).
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Appliquons le théorème de Pythagore à ce triangle BCD :
CD2 = BD2 + BC2 = 302 m2 + 402 m2 = 900 m2 + 1 600 m2 = 2 500 m2.
On en déduit que :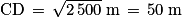 .
.
CD2 = BD2 + BC2 = 302 m2 + 402 m2 = 900 m2 + 1 600 m2 = 2 500 m2.
On en déduit que :
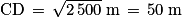 .
.2.
Soit l la longueur du demi-cercle de diamètre [CD].
La longueur d'un cercle de rayon r est égale à 2 × π × r.
On en déduit que : 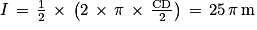 .
.
La longueur du parcours est :
AF + FE + ED + I + CB + BA
= 30 m + 80 m + 30 m + 25 π m + 40 m + 50 m
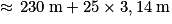
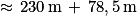
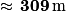 (valeur arrondie au mètre)
(valeur arrondie au mètre)
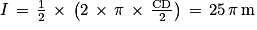 .
.La longueur du parcours est :
AF + FE + ED + I + CB + BA
= 30 m + 80 m + 30 m + 25 π m + 40 m + 50 m
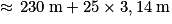
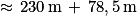
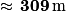 (valeur arrondie au mètre)
(valeur arrondie au mètre)3.
Dans un plan à l'échelle 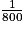 , toutes les longueurs réelles sont réduites 800 fois, donc divisées par 800.
, toutes les longueurs réelles sont réduites 800 fois, donc divisées par 800.
Par exemple, un segment de longueur réelle 80 m, soit 80 m ×100 = 8 000 cm est représenté par un segment de longueur 8 000 cm ÷ 800 = 10 cm.
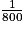 , toutes les longueurs réelles sont réduites 800 fois, donc divisées par 800.
, toutes les longueurs réelles sont réduites 800 fois, donc divisées par 800.Par exemple, un segment de longueur réelle 80 m, soit 80 m ×100 = 8 000 cm est représenté par un segment de longueur 8 000 cm ÷ 800 = 10 cm.
Pour calculer les dimensions sur le plan à l'échelle 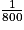 , on peut donc multiplier la dimension réelle en m par 100 pour la convertir en cm, puis la diviser par 800, ce qui revient à la multiplier par
, on peut donc multiplier la dimension réelle en m par 100 pour la convertir en cm, puis la diviser par 800, ce qui revient à la multiplier par 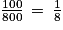 , donc à la diviser par 8.
, donc à la diviser par 8.
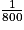 , on peut donc multiplier la dimension réelle en m par 100 pour la convertir en cm, puis la diviser par 800, ce qui revient à la multiplier par
, on peut donc multiplier la dimension réelle en m par 100 pour la convertir en cm, puis la diviser par 800, ce qui revient à la multiplier par 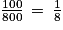 , donc à la diviser par 8.
, donc à la diviser par 8.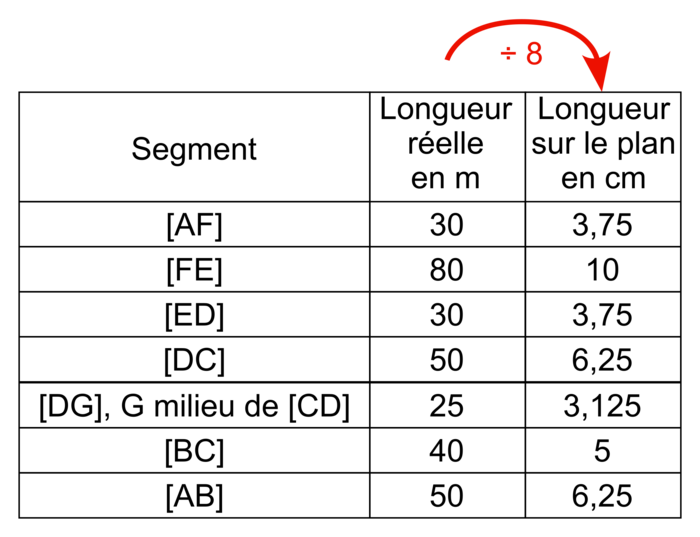 |
 |
4. 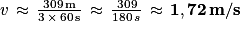
On sait que :
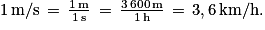
On en déduit :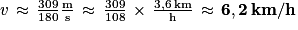 .
.
Autre procédure :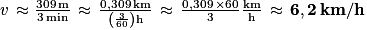 .
.
Killian a effectué son tour complet à la vitesse moyenne de 1,72 m/s (arrondie au centième), soit 6,2 km/h (arrondie au dixième).
Soit v la vitesse moyenne (non nulle) exprimée en mètres/seconde pour parcourir une distance d exprimée en mètres pendant un temps t (non nul) exprimé en secondes. Alors :
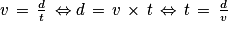
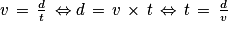
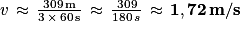
On sait que :
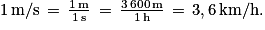
On en déduit :
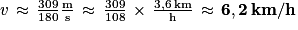 .
.Autre procédure :
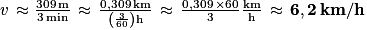 .
.Killian a effectué son tour complet à la vitesse moyenne de 1,72 m/s (arrondie au centième), soit 6,2 km/h (arrondie au dixième).
5.
a
Puisque Sophia court à vitesse constante, sa distance parcourue est proportionnelle au temps mis pour parcourir cette distance.
Utilisons un raisonnement basé sur les propriétés multiplicatives de la linéarité.
Utilisons un raisonnement basé sur les propriétés multiplicatives de la linéarité.
On consultera le document ressource « Résoudre des problèmes de proportionnalité au cycle 3 » sur https://eduscol.education.fr/document/16522/download
Sophia parcourt donc en 7 km = 7 000 m en 60 min ; elle parcourt 10 fois moins, c'est-à-dire 700 m, en 6 min ; et le triple, soit 700 m × 3 = 2 100 m en 18 min (le triple de 6 min).
Autre procédure :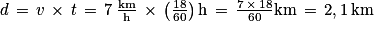 .
.
Comme la longueur d'un tour est 309 m environ, on calcule le quotient entier de 2 100 par 309 pour connaître le nombre de tours complets effectués. On trouve 6 tours, puisque 2 100 = 6 × 309 + 246.
Sophia a parcouru 6 tours complets (et 246 mètres) en 18 min.
Autre procédure :
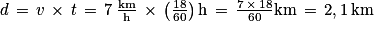 .
.Comme la longueur d'un tour est 309 m environ, on calcule le quotient entier de 2 100 par 309 pour connaître le nombre de tours complets effectués. On trouve 6 tours, puisque 2 100 = 6 × 309 + 246.
Sophia a parcouru 6 tours complets (et 246 mètres) en 18 min.
b.
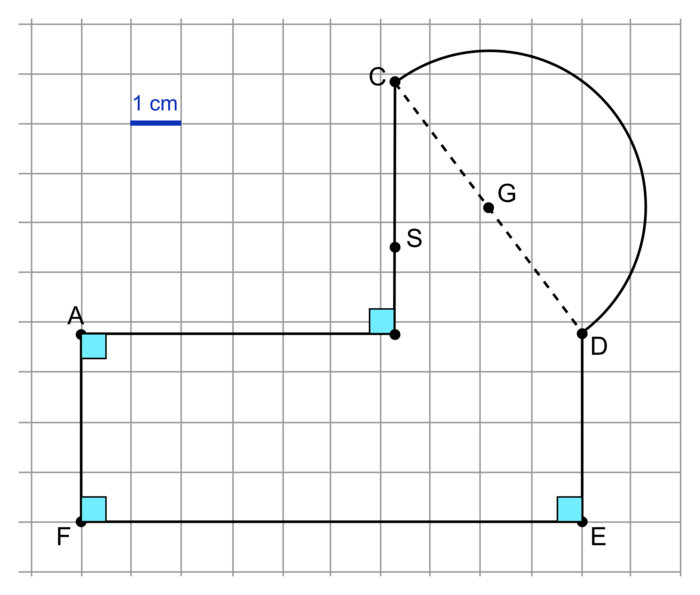
Un tour de parcours ayant pour longueur environ 309 m, il lui manque environ 309 m − 246 m = 63 m = 50 m + 13 m = AB + 13 m pour compléter son 7e tour.
Sur le plan, 13 m sont représentés par 1,625 cm.
Le point S sur le plan se trouve donc sur le segment [BC], à 1,625 cm de B.
Sur le plan, 13 m sont représentés par 1,625 cm.
Le point S sur le plan se trouve donc sur le segment [BC], à 1,625 cm de B.
 |
6.
a. Le nombre moyen de tours complets effectués est :
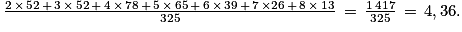
Dans cette école, les élèves ont parcouru en moyenne 4,36 tours.
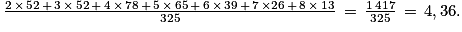
Dans cette école, les élèves ont parcouru en moyenne 4,36 tours.
b. L'étendue de cette série est la différence entre sa valeur maximale et sa valeur minimale, soit 8 tours − 2 tours = 6 tours.
c.
On appelle médiane d'une série, un nombre tel qu'il y a autant de valeurs inférieures à ce nombre que de valeurs supérieures.
La définition de la médiane est donnée sur Euler, le site des mathématiques de l'académie de Versailles : chercher dans la rubrique intitulée « Indicateurs de position ».
L'effectif total de la série est le nombre impair 325, de moitié 162,5.
Par définition, la médiane de cette série est la valeur prise par la 163e valeur de cette série, lorsqu'elles sont rangées dans l'ordre croissant.
En cumulant les premiers effectifs, on constate que la médiane est 4 tours.
Par définition, la médiane de cette série est la valeur prise par la 163e valeur de cette série, lorsqu'elles sont rangées dans l'ordre croissant.
| Nombre de tours (valeurs) | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Nombre d'élèves (effectifs) | 52 | 52 | 78 | 65 | 39 | 26 | 13 |
| Nombre d'élèves cumulés (effectifs cumulés croissants) | 52 | 104 | 182 | 247 | 286 | 312 | 325 |
En cumulant les premiers effectifs, on constate que la médiane est 4 tours.
d.
Il y a autant d'élèves qui ont parcouru un nombre égal ou inférieur à 4 tours que d'élèves ayant parcouru un nombre égal ou supérieur à 4 tours.
La définition du 1er et 3e quartile d'une série est donnée sur Euler, le site des mathématiques de l'académie de Versailles https://euler-ressources.ac-versailles.fr/wims/wims.cgi?session=3G6B09D7CB.2&+lang=fr&+module=adm%2Ftool%2Fglossary&+job=main&+cmd=new&+special_parm=mathematics%2Fstatistics%2Ffr%2Fquartile
Soit S une série statistique à une variable quantitative discrète ordonnée dans l'ordre croissant.
Le premier quartile de S est la plus petite valeur a de S telle qu'au moins 25 % des données soient inférieures ou égales à a ;
le troisième quartile de S est la plus petite valeur b de S telle qu'au moins 75 % des données soient inférieures ou égales à b.
Soit S une série statistique à une variable quantitative discrète ordonnée dans l'ordre croissant.
Le premier quartile de S est la plus petite valeur a de S telle qu'au moins 25 % des données soient inférieures ou égales à a ;
le troisième quartile de S est la plus petite valeur b de S telle qu'au moins 75 % des données soient inférieures ou égales à b.
e. Un quart de l'effectif total de cette série est 325 ÷ 4 = 81,25 arrondi à l'entier supérieur 82. Le premier quartile est la valeur prise par la 82e valeur de la série ordonnée dans l'ordre croissant, soit 3 tours.
De même, 81,25 × 3 = 243,75 arrondi à l'entier supérieur 244. Le 3e quartile est la valeur prise par la 244e valeur de la série ordonnée dans l'ordre croissant, soit 5 tours.
De même, 81,25 × 3 = 243,75 arrondi à l'entier supérieur 244. Le 3e quartile est la valeur prise par la 244e valeur de la série ordonnée dans l'ordre croissant, soit 5 tours.
f. 78 + 65 + 39 + 26 + 13 = 221.
221 élèves sur 325 élèves ont réussi à faire au moins 4 tours (donc 4 ou 5 ou 6 ou 7 ou 8 tours), soit un pourcentage de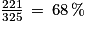 .
.
68 % des élèves ont réussi à faire au moins 4 tours.
221 élèves sur 325 élèves ont réussi à faire au moins 4 tours (donc 4 ou 5 ou 6 ou 7 ou 8 tours), soit un pourcentage de
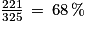 .
.68 % des élèves ont réussi à faire au moins 4 tours.
Exercice 2
On se reportera au document ressource des programmes « Espace et géométrie au cycle 3 - Les polygones »http://cache.media.education.gouv.fr/file/Geometrie/40/7/RA16_C3_MATH_Espace-geometrie_polygones_897407.pdf et notamment aux tableaux des pages 4, 5 et 6 sur les définitions et propriétés des quadrilatères.
1.
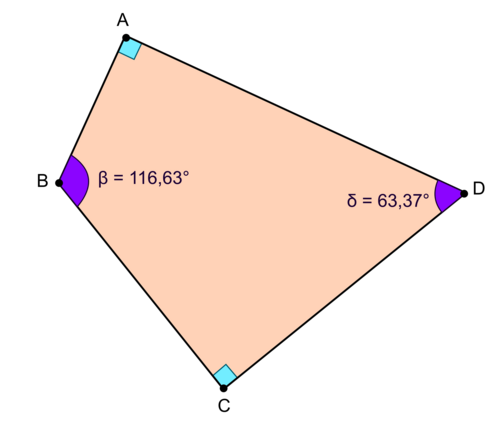
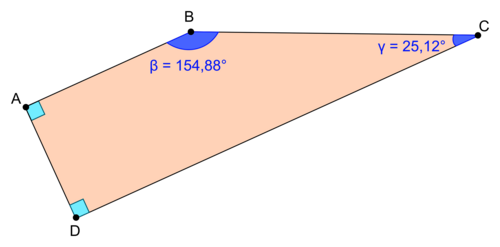
Un quadrilatère qui possède deux angles droits n'est pas nécessairement un rectangle, puisqu'il existe des quadrilatères qui possèdent exactement deux angles droits mais dont les deux autres angles ne sont pas droits.
Voici la représentation de deux d'entre eux :
Voici la représentation de deux d'entre eux :
 |
 |
2.
a.
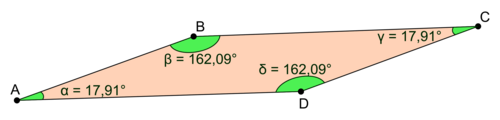
La réponse de l'élève A ne peut pas être admise comme définition mathématique du rectangle, puisqu'il existe des quadrilatères dont les côtés opposés ont la même longueur et qui ne sont pas des rectangles.
Par exemple, un parallélogramme dont les diagonales n'ont pas la même longueur, a bien des côtés opposés de même longueur mais ne possède pas d'angle droit.
Par exemple, un parallélogramme dont les diagonales n'ont pas la même longueur, a bien des côtés opposés de même longueur mais ne possède pas d'angle droit.
 |
b.
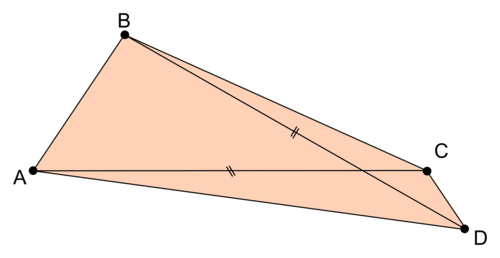
La réponse de l'élève B ne peut pas être admise comme définition mathématique du rectangle, puisqu'il existe des quadrilatères dont les diagonales sont de même longueur mais qui ne possèdent pas d'angle droit.
 |
3. Un rectangle est un parallélogramme particulier.
Un parallélogramme dont les diagonales sont perpendiculaires est un losange.
On en déduit qu'un rectangle dont les diagonales sont perpendiculaires est un carré, puisque c'est à la fois un rectangle et un losange.
Un parallélogramme dont les diagonales sont perpendiculaires est un losange.
On en déduit qu'un rectangle dont les diagonales sont perpendiculaires est un carré, puisque c'est à la fois un rectangle et un losange.
4. Le quadrilatère dessiné à main levée possède, d'après les codages, quatre côtés de même longueur : c'est donc par définition un losange.
Exercice 3
Il est nécessaire avant de se présenter au CRPE de s'entraîner à la programmation, si possible avec Scratch (en ligne https://scratch.mit.edu/download/scratch2) dont vous remarquez dans l'adresse qu'il a été développé par le MIT (pour les enfants).
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4 https://eduscol.education.fr/document/17311/download
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4 https://eduscol.education.fr/document/17311/download
Remarque : Si vous souhaitez recopier ce script sur Scratch, n'oubliez pas de créer quatre variables a, b, c et d avant la 3e ligne : voici les couleurs pour vous aider.
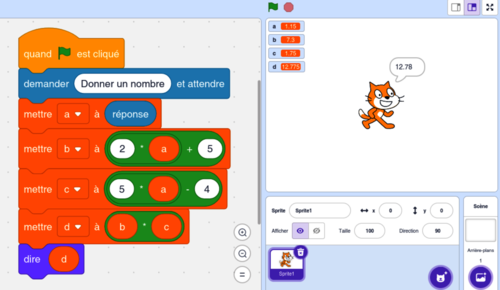 |
1. Si l'utilisateur saisit le nombre 2, alors a = 2 ; b = 2 × 2 + 5 = 9 ; c = 5 × 2 − 4 = 6 et d = b × c = 9 × 6 = 54.
2. Si l'utilisateur saisit le nombre 1,15, alors a = 1,15 ; b = 2 × 1,15 + 5 = 7,3 ; c = 5 × 1,15 − 4 = 1,75 et d = b × c = 7,3 × 1,75 = 12,775.
3.
Le programme A retourne le nombre 0 si le produit d = b × c = 0
Un produit de facteurs est nul si et seulement si l'un au moins des facteurs est nul.
b × c = 0 si b = 0 ou c = 0.
Or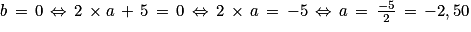 .
.
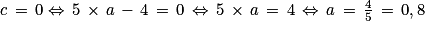 .
.
On en déduit que le programme A retourne le nombre 0 si l'utilisateur saisit le nombre −2,5 ou s'il saisit le nombre 0,8.
Or
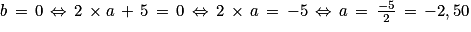 .
.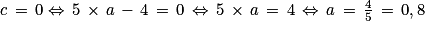 .
.On en déduit que le programme A retourne le nombre 0 si l'utilisateur saisit le nombre −2,5 ou s'il saisit le nombre 0,8.
4.
a. Si l'utilisateur saisit le nombre 3 avec le programme B, alors le programme retourne le nombre (3 × 2 + 5)2 = 112 = 121.
b. Si l'utilisateur saisit le nombre 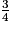 avec le programme B, alors le programme retourne le nombre
avec le programme B, alors le programme retourne le nombre 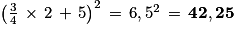 .
.
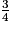 avec le programme B, alors le programme retourne le nombre
avec le programme B, alors le programme retourne le nombre 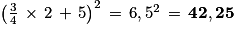 .
.5.
Vous devez savoir utiliser les fonctions habituelles d'un tableur (voir par exemple http://www.clg-monnet-briis.ac-versailles.fr/Utiliser-un-tableur), ce qui vous permettra aussi de cerner la notion de variable, comme précisé dans le document « Utiliser le calcul littéral » sur https://eduscol.education.fr/document/17263/download
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
a. On retrouve la réponse à la question 4.a. dans la cellule D2.
b. On peut saisir dans la cellule A2 afin de la copier-glisser sur la ligne 2 la formule :
« =PUISSANCE(A1*2+5 ; 2) » ou « =(A1*2+5)*(A1*2+5) ».
Remarque : ne pas oublier de commencer une formule par =.
« =PUISSANCE(A1*2+5 ; 2) » ou « =(A1*2+5)*(A1*2+5) ».
Remarque : ne pas oublier de commencer une formule par =.
6.
a. Soit x le nombre saisi par l'utilisateur ; B retourne le nombre 0 si et seulement si 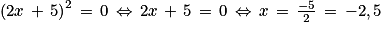 donc si l'utilisateur a saisi le nombre −2,5.
donc si l'utilisateur a saisi le nombre −2,5.
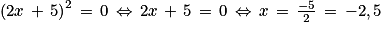 donc si l'utilisateur a saisi le nombre −2,5.
donc si l'utilisateur a saisi le nombre −2,5.b.
On retrouvera les définitions des différents types de nombre sur le document ressource du programme de cycle 3 « Fractions et nombres décimaux au cycle 3 » à partir de la page 5 https://eduscol.education.fr/document/16510/download
Le nombre 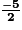 est rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers.
est rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers.
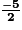 est rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers.
est rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers.c. Le nombre 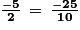 est décimal, puisqu'il peut s'écrire sous la forme d'une fraction décimale (fraction dont le dénominateur est une puissance de 10, comme 10, 100, 1 000, etc.).
est décimal, puisqu'il peut s'écrire sous la forme d'une fraction décimale (fraction dont le dénominateur est une puissance de 10, comme 10, 100, 1 000, etc.).
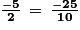 est décimal, puisqu'il peut s'écrire sous la forme d'une fraction décimale (fraction dont le dénominateur est une puissance de 10, comme 10, 100, 1 000, etc.).
est décimal, puisqu'il peut s'écrire sous la forme d'une fraction décimale (fraction dont le dénominateur est une puissance de 10, comme 10, 100, 1 000, etc.).7.
On pourra consulter le diaporama sur la résolution d'équation sur https://maths.enseigne.ac-lyon.fr/spip/spip.php?article206, puis visionner https://www.lumni.fr/video/resoudre-une-equation-revisions-brevet-mathematiques
Appelons x le nombre saisi par l'utilisateur dans les programmes A et B qui retournent le même nombre. Le problème peut se traduire par l'équation :
![\left ( 2x\, +\, 5 \right )\left ( 5x\, -\, 4 \right )\, =\, \left ( 2x\, +\, 5 \right )^{2}\, \Leftrightarrow \, \left ( 2x\, +\, 5 \right )\left [ \left ( 5x\, - 4\right )-\, \left ( 2x\,+\, 5 \right ) \right ]\, =\, 0](https://media.cap-concours.fr/cens/images/a_m056_m26.png)
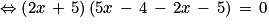
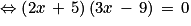
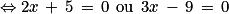
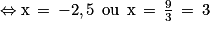
![\left ( 2x\, +\, 5 \right )\left ( 5x\, -\, 4 \right )\, =\, \left ( 2x\, +\, 5 \right )^{2}\, \Leftrightarrow \, \left ( 2x\, +\, 5 \right )\left [ \left ( 5x\, - 4\right )-\, \left ( 2x\,+\, 5 \right ) \right ]\, =\, 0](https://media.cap-concours.fr/cens/images/a_m056_m26.png)
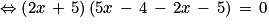
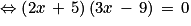
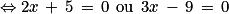
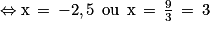
Vérifions :
On sait déjà que si l'utilisateur saisit le nombre −2,5, alors les deux programmes retournent le nombre 0.
Si l'utilisateur saisit le nombre 3, alors le programme A retourne le nombre (2 × 3 + 5) (5 × 3 − 4) = 11 × 11 = 121, qui est bien le même nombre retourné par le programme B d'après les questions précédentes.
Les programmes A et B retournent le même nombre si l'utilisateur saisit l'un des deux nombres −2,5 ou 3.
On sait déjà que si l'utilisateur saisit le nombre −2,5, alors les deux programmes retournent le nombre 0.
Si l'utilisateur saisit le nombre 3, alors le programme A retourne le nombre (2 × 3 + 5) (5 × 3 − 4) = 11 × 11 = 121, qui est bien le même nombre retourné par le programme B d'après les questions précédentes.
Les programmes A et B retournent le même nombre si l'utilisateur saisit l'un des deux nombres −2,5 ou 3.
Exercice 4
1.
La grille contient 8 × 8 = 64 cases.
On peut associer le jeu à une expérience aléatoire dont chaque issue est donnée par chacune des coordonnées d'une case, les 64 issues étant équiprobables.
On peut associer le jeu à une expérience aléatoire dont chaque issue est donnée par chacune des coordonnées d'une case, les 64 issues étant équiprobables.
Si toutes les issues sont équiprobables, la probabilité d'un événement se calcule par :
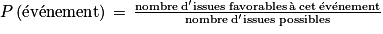
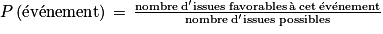
a. Jeanne touche un bateau si elle donne les coordonnées de l'une des 12 cases grisées par un bateau, donc avec une probabilité de 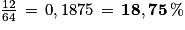 .
.
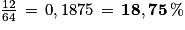 .
.b. Jeanne ne touche aucun bateau si elle donne les coordonnées de l'une des 64 − 12 = 52 cases blanches, donc avec une probabilité de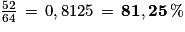 .
.
Autre procédure : « Ne toucher aucun bateau » est l'événement contraire de « toucher un bateau », donc sa probabilité est 100 % − 18,75 % = 81,25 %.
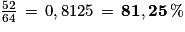 .
.Autre procédure : « Ne toucher aucun bateau » est l'événement contraire de « toucher un bateau », donc sa probabilité est 100 % − 18,75 % = 81,25 %.
c. 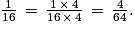
Un bateau qui a une chance sur 16 d'être touché occupe 4 cases sur la grille.
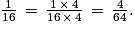
Un bateau qui a une chance sur 16 d'être touché occupe 4 cases sur la grille.
d. La colonne B comporte 8 cases, dont 4 sont grisées par un bateau. Sachant qu'elle choisit la colonne B, Jeanne a 4 chances sur 8, soit une probabilité de 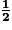 de toucher un bateau.
de toucher un bateau.
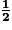 de toucher un bateau.
de toucher un bateau.2. Il y a 3 cases adjacentes par un côté à la case E1 : D1, E2 et F1. Seule la case F1 est grisée. On en déduit que la probabilité que Jeanne coule ce bateau de deux cases, sachant qu'elle l'a touché auparavant, est 1 chance sur 3, soit une probabilité de 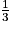 .
.
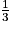 .
.3. Jeanne a déjà désigné deux cases blanches : il lui reste à désigner l'une des 62 cases restantes, dont 12 sont grisées par un bateau. Elle a donc une probabilité de 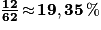 de toucher un bateau.
de toucher un bateau.
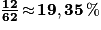 de toucher un bateau.
de toucher un bateau.Exercice 5
1. 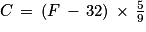
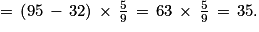
95 °F correspondent à 35 °C.
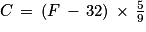
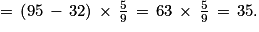
95 °F correspondent à 35 °C.
2. 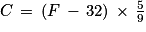 et C = 5, d'où :
et C = 5, d'où :
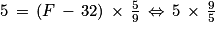
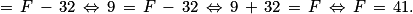
5 °C correspondent à 41 °F.
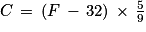 et C = 5, d'où :
et C = 5, d'où :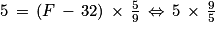
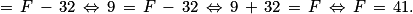
5 °C correspondent à 41 °F.
3. 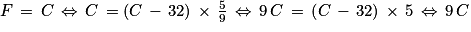
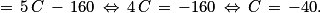
Vérification :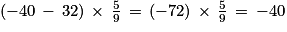 .
.
−40 °C correspondent à −40 °F.
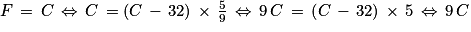
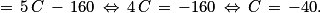
Vérification :
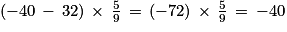 .
.−40 °C correspondent à −40 °F.
Exercice 6
1. Pour effectuer avec la même méthode, le produit 6 × 8, on lève 5 orteils et 1 doigt avec le pied et la main gauche, puis 5 orteils et 3 doigts avec le pied et la main droite.
On a donc 1 + 3 = 4 doigts levés ; le résultat recherché comporte 4 dizaines.
Le produit des doigts baissés de la main gauche et de la main droite est égal à (5 − 1) × (5 − 3) = 4 × 2 = 80 ; le résultat recherché comporte 8 unités.
Le résultat recherché est égal à 40 + 8 = 48.
On a donc 1 + 3 = 4 doigts levés ; le résultat recherché comporte 4 dizaines.
Le produit des doigts baissés de la main gauche et de la main droite est égal à (5 − 1) × (5 − 3) = 4 × 2 = 80 ; le résultat recherché comporte 8 unités.
Le résultat recherché est égal à 40 + 8 = 48.
2.
a. (5 − g) représente le nombre de doigts baissés de la main gauche et (5 − d) le nombre de doigts baissés de la main droite.
b.
On utilise la double distributivité pour développer les produits :
Quels que soient les nombres a, b, c et d :
(a + b)(c + d) = ac + ad + bc + bd
(a − b)(c + d) = ac + ad − bc − bd
(a + b)(c − d) = ac − ad + bc − bd
(a − b)(c − d) = ac − ad − bc + bd
(a + b)(c + d) = ac + ad + bc + bd
(a − b)(c + d) = ac + ad − bc − bd
(a + b)(c − d) = ac − ad + bc − bd
(a − b)(c − d) = ac − ad − bc + bd
(5 + g)(5 + d) = 25 + 5d + 5g + gd
10(g + d) + (5 − g)(5 − d) = 10 g + 10 d + 25 − 5 d − 5 g + gd = 25 + 5 d + 5 g + gd
Conclusion : (5 + g)(5 + d) = 10(g + d) + (5 − g)(5 − d).
10(g + d) + (5 − g)(5 − d) = 10 g + 10 d + 25 − 5 d − 5 g + gd = 25 + 5 d + 5 g + gd
Conclusion : (5 + g)(5 + d) = 10(g + d) + (5 − g)(5 − d).
c. (5 + g)(5 + d) représente le produit à effectuer, chaque facteur entier compris entre 5 et 10 étant écrit sous la forme de la somme des 5 (orteils) et du nombre de doigts levés du même côté que les orteils.
10(g + d) représente 10 fois la somme des doigts levés, donc un nombre de dizaines compris dans le produit recherché.
(5 − g)(5 − d) représente le produit des doigts baissés de chaque main.
La somme de ces deux nombres correspond par conséquent au produit recherché.
10(g + d) représente 10 fois la somme des doigts levés, donc un nombre de dizaines compris dans le produit recherché.
(5 − g)(5 − d) représente le produit des doigts baissés de chaque main.
La somme de ces deux nombres correspond par conséquent au produit recherché.
Document précédent
Sujet 2023 de mathématiques, groupement académique 1
Document suivant
Sujet 2023 de mathématiques, groupement académique 3
