Dernier essai le
- Score :
/20
Ce sujet est composé de cinq exercices indépendants.
Exercice 1
1. L'entier 4 216 est-il un multiple de 17 ? Justifier.
2.
Guillaume veut revoir sa leçon en prenant son petit déjeuner. Malheureusement, il a renversé son chocolat sur sa feuille. Le chiffre des unités et la justification de l'exemple du maître, sont illisibles…
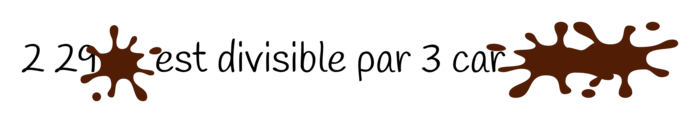 |
a. Rappeler le critère de divisibilité par 3.
b. Donner toutes les valeurs possibles du chiffre des unités, caché par la tache située à gauche.
3.
On admet qu'un nombre entier n est divisible par 7 si et seulement si la différence entre son nombre de dizaines et le double de son chiffre des unités est un multiple 7, positif ou négatif.
Par exemple, 294 est divisible par 7, car 29 − 4 × 2 = 21, et 21 est divisible par 7.
Par exemple, 294 est divisible par 7, car 29 − 4 × 2 = 21, et 21 est divisible par 7.
a. En détaillant les étapes, vérifier que 413 est bien divisible par 7 en utilisant le critère indiqué ci-dessus.
b. Le nombre 5 292 est-il divisible par 7 ? Répondre en appliquant, plusieurs fois si nécessaire, le critère précédent.
c.
Pour déterminer si 1 138 984 est divisible par 7, on utilise le critère précédent à l'aide d'un tableur. On rappelle que la fonction ENT renvoie la partie entière d'un nombre.
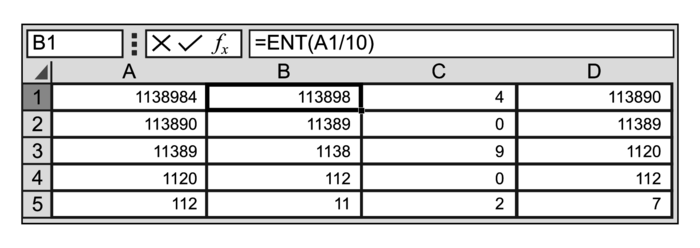 |
Dans la cellule B1, on a saisi la formule : « = ENT(A1/10) ».
Observer la feuille de calcul, puis indiquer des formules ayant pu être saisies dans les cellules C1 et D1 qui, étirées vers le bas de la feuille de calcul, permettent d'obtenir directement la feuille de calcul ci-dessus.
Observer la feuille de calcul, puis indiquer des formules ayant pu être saisies dans les cellules C1 et D1 qui, étirées vers le bas de la feuille de calcul, permettent d'obtenir directement la feuille de calcul ci-dessus.
d. Le nombre 1 138 984 est-il divisible par 7 ? Justifier en interprétant les résultats fournis par la feuille de calcul.
Exercice 2
1.
Nadia se prépare pour le cross organisé par son école dont le parcours, ABIFCDE, est représenté ci-contre.
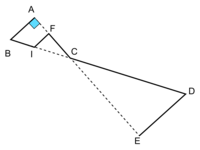 |
Les droites (AE) et (BD) se coupent en C.
![\mathrm{F}\, \in \, \left [ \mathrm{AC} \right ]](https://media.cap-concours.fr/cens/images/a_m057_m1.png) et
et ![\mathrm{I}\, \in \, \left [ \mathrm{BC} \right ]](https://media.cap-concours.fr/cens/images/a_m057_m2.png) .
.
Les droites (AB), (FI) et (DE) sont parallèles.
ABC est un triangle rectangle en A.
AB = 300 m ; AC = 400 m ; CD = 1250 m et IC = 350 m.
![\mathrm{F}\, \in \, \left [ \mathrm{AC} \right ]](https://media.cap-concours.fr/cens/images/a_m057_m1.png) et
et ![\mathrm{I}\, \in \, \left [ \mathrm{BC} \right ]](https://media.cap-concours.fr/cens/images/a_m057_m2.png) .
.Les droites (AB), (FI) et (DE) sont parallèles.
ABC est un triangle rectangle en A.
AB = 300 m ; AC = 400 m ; CD = 1250 m et IC = 350 m.
a. Déterminer la longueur BC.
b. Déterminer les longueurs IF et CF.
c. Déterminer la longueur ED.
d. Calculer la longueur du parcours ABIFCDE.
2.
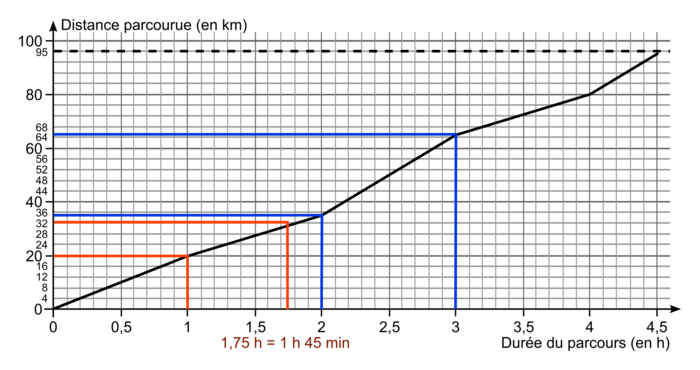
Quentin, un adolescent de 16 ans, fait du vélo. On a représenté ci-dessous la distance parcourue en fonction de la durée de parcours lors de sa dernière sortie.
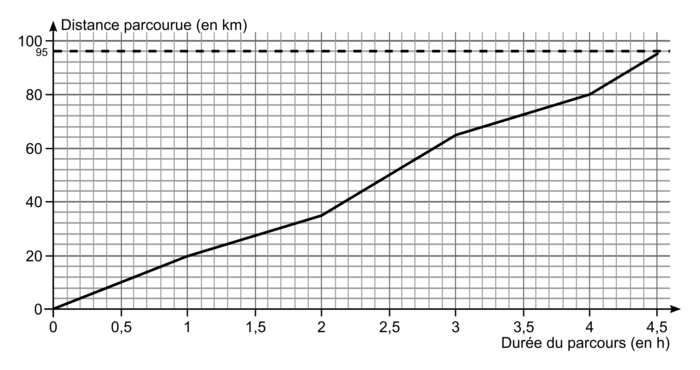 |
a. La durée du parcours en heures est-elle proportionnelle à la distance parcourue en kilomètres ? Justifier.
Les réponses aux questions suivantes seront données avec la précision permise par le graphique.
Les réponses aux questions suivantes seront données avec la précision permise par le graphique.
b. Quelle distance a parcouru Quentin en 1 h ?
c. Déterminer la vitesse moyenne de Quentin durant la première heure, en mètres par seconde, avec un arrondi au centième.
d. Quelle distance a parcouru Quentin en 1 h 45 ?
e. Estimer la vitesse de Quentin durant la troisième heure de son parcours, en kilomètre par heure.
f. Peut-on affirmer que sa vitesse moyenne lors de la troisième heure est supérieure de plus de 40 % à sa vitesse moyenne lors de la première heure ? Justifier.
g. Quelle est la vitesse moyenne de Quentin lors de cette sortie, en kilomètres par heure, avec un arrondi au centième.
Exercice 3
Un enseignant de CM2 souhaite créer avec ses élèves des décorations pour la salle de classe.
1.
Un premier groupe fabriquera une guirlande constituée d'un motif proposé par l'enseignant dans le script ci-dessous.
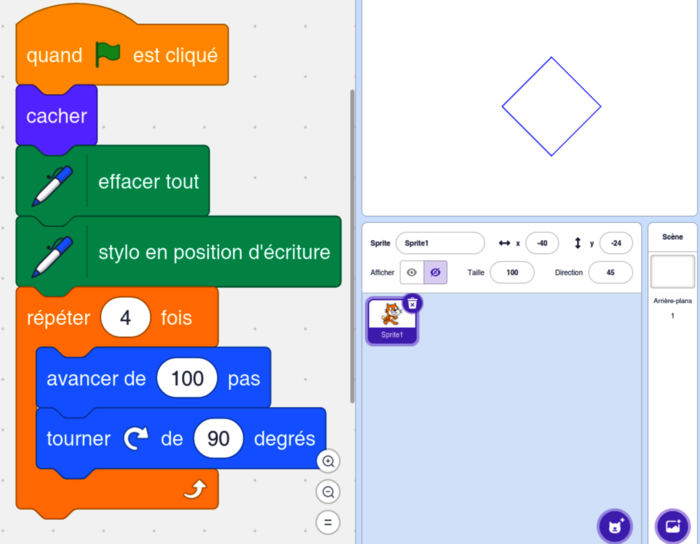 |
En voyant apparaître la figure :
• Pierre dit : « C'est un losange. »
• Ana dit : « Ce n'est pas un rectangle. »
• Karim dit : « C'est un quadrilatère. »
• Lucie dit : « C'est un carré. »
En utilisant le script et les propriétés des quadrilatères, dire si chaque affirmation est vraie ou fausse en justifiant.
2.
La longueur des côtés du pentagone obtenu est proportionnelle à la longueur du segment [RS] choisi au départ. En choisissant un segment [RS] de longueur 4 cm, on obtient un pentagone dont les côtés mesurent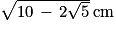 .
.
Un second groupe fabriquera des étoiles. L'enseignant leur a montré comment dessiner une étoile à cinq branches sur GeoGebra en utilisant un pentagone.
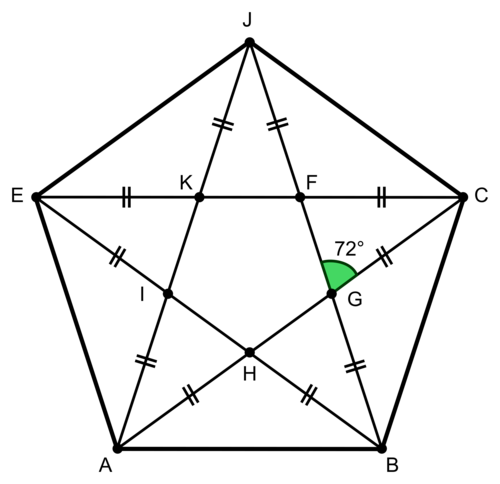 |
Pour pouvoir construire des pentagones avec la règle et le compas, il propose le programme de construction ci-dessous.
| Tracer un segment [RS]. Placer le point O au milieu du segment [RS]. Tracer le cercle de diamètre [RS]. Soit L un point de ce cercle tel que 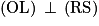 . .Placer le point I au milieu du segment [OS]. Le cercle de centre I et de rayon [IL] coupe le segment [RO] en D. LD est la longueur des côtés du pentagone régulier inscrit dans le cercle de diamètre [RS], placer les 5 sommets du pentagone sur le cercle. Construire le pentagone. |
La longueur des côtés du pentagone obtenu est proportionnelle à la longueur du segment [RS] choisi au départ. En choisissant un segment [RS] de longueur 4 cm, on obtient un pentagone dont les côtés mesurent
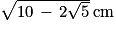 .
.a. Montrer que pour obtenir un pentagone dont les côtés mesurent 7 cm, il faut commencer par construire un segment [RS] mesurant environ 11,9 cm.
b. En utilisant le programme de construction précédent, construire un pentagone régulier LMNPQ dont les côtés mesurent 7 cm.
Puis, il leur montre l'étoile à cinq branches ci-contre, obtenue en utilisant le logiciel Scratch :
Puis, il leur montre l'étoile à cinq branches ci-contre, obtenue en utilisant le logiciel Scratch :
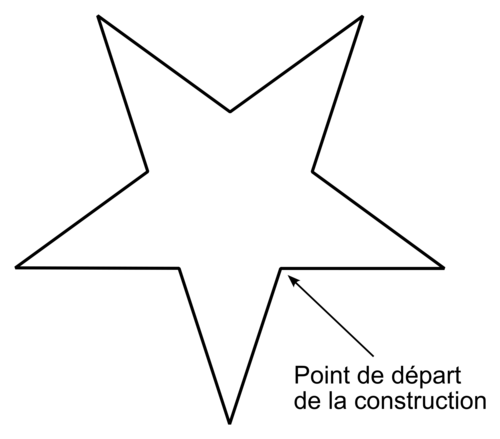 |
c.
Recopier et compléter les lignes 7 et 9 du script utilisé pour construire l'étoile.
On rappelle que lorsque le lutin est orienté à 90°, cela signifie qu'il va se déplacer vers la droite.
On rappelle que lorsque le lutin est orienté à 90°, cela signifie qu'il va se déplacer vers la droite.
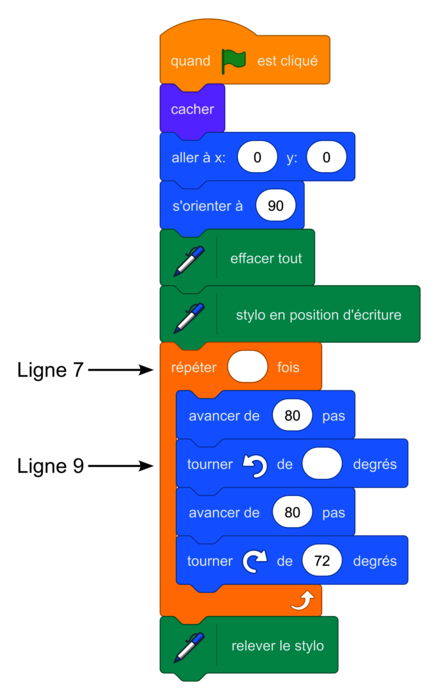 |
d. Quel est le périmètre, en pas, de cette étoile ?
e. L'enseignant souhaite doubler le périmètre de son étoile. Recopier les quatre lignes à l'intérieur du bloc « répéter », lignes 8 à 11, en apportant les modifications nécessaires pour obtenir cette nouvelle étoile.
Exercice 4
Dans une classe de Grande Section, l'enseignant propose à ses élèves le jeu suivant dans lequel il s'agit d'être le premier à avoir exactement 15 jetons (source : Découvrir les maths GS – Éditions Hatier).
Chaque élève lance deux dés bien équilibrés, identiques, à 6 faces numérotées de 1 à 6. Il considère les deux nombres indiqués sur les faces supérieures de chacun des dés.
Lorsque les deux dés indiquent le même nombre, l'élève prend autant de jetons que l'indique l'un des deux dés. Sinon, il prend autant de jetons que le plus grand des deux nombres ou le double de jetons du plus petit.
Après avoir lancé les dés, un élève a la possibilité de passer son tour. Dans ce cas, il ne prend aucun jeton.
Chaque élève lance deux dés bien équilibrés, identiques, à 6 faces numérotées de 1 à 6. Il considère les deux nombres indiqués sur les faces supérieures de chacun des dés.
Lorsque les deux dés indiquent le même nombre, l'élève prend autant de jetons que l'indique l'un des deux dés. Sinon, il prend autant de jetons que le plus grand des deux nombres ou le double de jetons du plus petit.
Après avoir lancé les dés, un élève a la possibilité de passer son tour. Dans ce cas, il ne prend aucun jeton.
1. Un élève lance les deux dés ; il obtient un 3 et un 2. Combien de jetons peut-il prendre ? Donner tous les cas possibles.
2. Dresser la liste des tirages permettant d'obtenir 3 jetons.
3.
Un élève lance les deux dés.
a. Montrer que la probabilité de l'événement « les nombres obtenus sont un 3 et un 2 » est 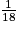 .
.
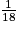 .
.b. Quelle est la probabilité de l'événement « au moins un des nombres obtenus est 3 » ?
c. Quelle est la probabilité de l'événement « les nombres obtenus permettent de prendre 4 jetons » ?
4. Après un nouveau lancer des deux dés, un élève a pris 3 jetons. Au lancer suivant, la probabilité qu'il prenne de nouveau 3 jetons augmente-t-elle, reste-t-elle identique ou diminue-t-elle par rapport à la probabilité d'avoir pris 3 jetons au tirage précédent ? Justifier.
5. En fin de partie, un élève possède 12 jetons. Lors de son lancer de dés, il obtient un 1 et un 4. Pourquoi est-il préférable pour lui de passer son tour ?
Exercice 5
Pour chaque affirmation, indiquer si elle est vraie ou fausse. Justifier.
Affirmation 1 : « 257 est un nombre décimal. »
Affirmation 2 : «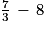 est un nombre rationnel. »
est un nombre rationnel. »
Affirmation 3 : « La somme de trois nombres entiers consécutifs est toujours un multiple de 3. »
Affirmation 4 : « L'équation (x + 1)(x − 2) = (x − 3)(x + 4) admet un nombre entier comme solution. »
Affirmation 5 : « Augmenter une quantité de 15 % puis de 10 % revient à l'augmenter de son quart. »
Affirmation 6 : « Un quadrilatère ayant un angle droit est un rectangle. »
Affirmation 7 : « Un triangle rectangle peut être équilatéral. »
Affirmation 8 : « Par la fonction f définie par f(x) = − 3x + 1, l'antécédent de 4 est − 11. »
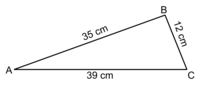
Affirmation 9 : « Le triangle ABC, schématisé ci-dessous, est rectangle. »
Affirmation 2 : «
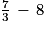 est un nombre rationnel. »
est un nombre rationnel. »Affirmation 3 : « La somme de trois nombres entiers consécutifs est toujours un multiple de 3. »
Affirmation 4 : « L'équation (x + 1)(x − 2) = (x − 3)(x + 4) admet un nombre entier comme solution. »
Affirmation 5 : « Augmenter une quantité de 15 % puis de 10 % revient à l'augmenter de son quart. »
Affirmation 6 : « Un quadrilatère ayant un angle droit est un rectangle. »
Affirmation 7 : « Un triangle rectangle peut être équilatéral. »
Affirmation 8 : « Par la fonction f définie par f(x) = − 3x + 1, l'antécédent de 4 est − 11. »
Affirmation 9 : « Le triangle ABC, schématisé ci-dessous, est rectangle. »
 |
Affirmation 10 : « Si on multiplie par 3 les longueurs des côtés d'un rectangle, alors son aire est également multipliée par 3. »
Corrigé
Corrigé
Exercice 1
1. Effectuons la division euclidienne de 4 216 par 17 : on obtient l'égalité caractéristique 4 216 = 17 × 248 + 0. Comme le reste est nul, 4 216 est un multiple de 17.
2.
a. Un nombre entier est divisible par 3 si et seulement si la somme de ses chiffres est divisible par 3.
b. Soit u le chiffre des unités du nombre N de quatre chiffres de la leçon : N est divisible par 3 si et seulement si la somme de ses chiffres 2 + 2 + 9 + u = 13 + u est elle-même divisible par 3. u étant un entier compris entre 0 et 9, 13 + u est divisible par 3 si et seulement si ou ou u = 2 ou u = 5 ou u = 8.
3.
a. 413 a pour nombre de dizaines 41 et pour chiffre des unités 3 ;
41 − 3 × 2 = 41 − 6 = 35 = 7 × 5.
Puisque 35 est divisible par 7, le nombre 413 est lui-même divisible par 7.
41 − 3 × 2 = 41 − 6 = 35 = 7 × 5.
Puisque 35 est divisible par 7, le nombre 413 est lui-même divisible par 7.
b. 5 292 a pour nombre de dizaines 529 et pour chiffre des unités 2 ;
529 − 2 × 2 = 529 − 4 = 525.
525 a pour nombre de dizaines 52 et pour chiffre des unités 5 ;
52 − 5 × 2 = 52 − 10 = 42 = 7 × 6.
Puisque 42 est divisible par 7, le nombre 525 est lui-même divisible par 7.
Puisque 525 est divisible par 7, le nombre 5 292 est lui-même divisible par 7.
529 − 2 × 2 = 529 − 4 = 525.
525 a pour nombre de dizaines 52 et pour chiffre des unités 5 ;
52 − 5 × 2 = 52 − 10 = 42 = 7 × 6.
Puisque 42 est divisible par 7, le nombre 525 est lui-même divisible par 7.
Puisque 525 est divisible par 7, le nombre 5 292 est lui-même divisible par 7.
c.
Vous devez savoir utiliser les fonctions habituelles d'un tableur (voir par exemple http://www.clg-monnet-briis.ac-versailles.fr/Utiliser-un-tableur), ce qui vous permettra aussi de cerner la notion de variable, comme précisé dans le document « Utiliser le calcul littéral » sur https://eduscol.education.fr/document/17263/download
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
La cellule B1 contient le nombre de dizaines de l'entier N contenu dans la cellule A1. On calcule ensuite le chiffre des unités du nombre N en saisissant la formule « =A1−10*B1 » ou bien « =MOD(A1;10) » qui renvoie le reste de la division euclidienne du nombre contenu dans la cellule A1 par 10. On peut ensuite calculer la différence entre le nombre d'unités de N et le double de son chiffre des unités, en saisissant dans la cellule D2 la formule « =B1−2*C1 ».
d. Le nombre 1 138 984 est divisible par 7.
En effet,
7 = 7 × 1 est divisible par 7 ;
donc 112 = 10 × 11 + 2 l'est aussi, puisque 11 − 2 × 2 = 7 ;
donc 1 120 = 10 × 112 + 0 l'est aussi, puisque 112 − 0 × 2 = 112 ;
donc 11 389 = 10 × 1 138 + 8 l'est aussi, puisque 1 138 − 8 × 2 = 1 120 ;
donc 113 890 = 10 × 11 389 + 0 l'est aussi, puisque 11 389 − 0 × 2 = 11 389 ;
donc 1 138 894 = 10 × 113 898 + 4 l'est aussi, puisque 113 898 − 4 × 2 = 113 890.
En effet,
7 = 7 × 1 est divisible par 7 ;
donc 112 = 10 × 11 + 2 l'est aussi, puisque 11 − 2 × 2 = 7 ;
donc 1 120 = 10 × 112 + 0 l'est aussi, puisque 112 − 0 × 2 = 112 ;
donc 11 389 = 10 × 1 138 + 8 l'est aussi, puisque 1 138 − 8 × 2 = 1 120 ;
donc 113 890 = 10 × 11 389 + 0 l'est aussi, puisque 11 389 − 0 × 2 = 11 389 ;
donc 1 138 894 = 10 × 113 898 + 4 l'est aussi, puisque 113 898 − 4 × 2 = 113 890.
Exercice 2
1.
a.
Propriété de Pythagore (permettant de calculer la longueur d'un côté d'un triangle rectangle quand on connaît la longueur de ses deux autres côtés).
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
On applique la propriété de Pythagore au triangle ABC rectangle en A :
BC2 = AB2 + AC2 = (300 m)2 + (400 m)2 = 250 000 m2.
On en déduit que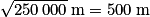 .
.
La longueur BC est égale à 500 m.
BC2 = AB2 + AC2 = (300 m)2 + (400 m)2 = 250 000 m2.
On en déduit que
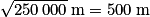 .
.La longueur BC est égale à 500 m.
b.
On pourra réviser la propriété (ou théorème) de Thalès sur https://blogpeda.ac-bordeaux.fr/aromaths/files/2014/03/le%C3%A7on-7-Le-th%C3%A9or%C3%A8me-de-Thal%C3%A8s-et-sa-r%C3%A9ciproque.pdf et visionner une vidéo de Lumini, comme https://www.lumni.fr/video/a-quoi-sert-le-theoreme-de-thales
Considérons les triangles ABC et IFC, avec F un point de [AC] et I un point de [BC] : puisque les droites (FI) et (AB) sont parallèles, d'après le théorème de Thalès, on a :
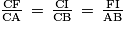
On en déduit que :
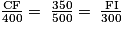
Puis que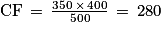 et
et 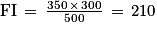 , on a :
, on a :
CF = 280 m et FI = 210 m.
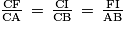
On en déduit que :
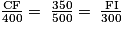
Puis que
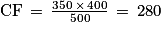 et
et 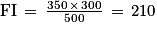 , on a :
, on a :CF = 280 m et FI = 210 m.
c. Considérons les triangles ABC et CDE (en configuration « papillon »), avec D un point de la demi-droite [BC) et E un point de la demi-droite [AC).
Puisque les droites (AB) et (DE) sont parallèles, d'après le théorème de Thalès, on a :
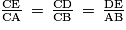
On en déduit que :
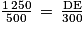
Puis que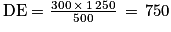 .
.
DE = 750 m.
Puisque les droites (AB) et (DE) sont parallèles, d'après le théorème de Thalès, on a :
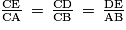
On en déduit que :
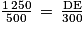
Puis que
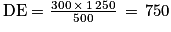 .
.DE = 750 m.
d. La longueur du parcours ABIFCDE est :
AB + BI + IF + FC + CD + DE
= 300 m + 150 m + 210 m + 280 m + 1 250 m + 750 m = 2 940 m
(car I est un point de [BC] donc BI = BC −IC = 500 −350 = 150 m).
AB + BI + IF + FC + CD + DE
= 300 m + 150 m + 210 m + 280 m + 1 250 m + 750 m = 2 940 m
(car I est un point de [BC] donc BI = BC −IC = 500 −350 = 150 m).
2.
a. La durée du parcours en heures n'est pas proportionnelle à la distance parcourue en km, puisque la représentation graphique de la durée en fonction de la distance n'est pas une droite.
b. Sur le graphique, on lit que Quentin a parcouru 20 km en 1 h.
c.
 |
Soit v la vitesse moyenne (non nulle) exprimée en km/h pour parcourir une distance d exprimée en km pendant un temps t (non nul) exprimé en h, alors :
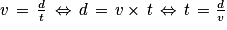
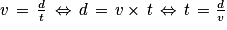
Pendant la 1re heure, la vitesse moyenne de Quentin est donc 20 km/h.
Or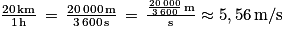 .
.
Pendant la première heure, Quentin roule à la vitesse moyenne de 5,56 m/s, arrondie au centième.
Or
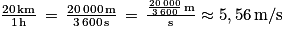 .
.Pendant la première heure, Quentin roule à la vitesse moyenne de 5,56 m/s, arrondie au centième.
d. Sur le graphique, on lit que Quentin a parcouru environ 32 km en 1 h 45 min = 1,75 h.
e. D'après la lecture graphique, en 2 heures, Quentin a parcouru environ 35 km, et 65 km en 3 h.
Il a donc parcouru 65 km − 35 km = 30 km pendant la troisième heure de son parcours, avec une vitesse moyenne de 30 km/h.
Il a donc parcouru 65 km − 35 km = 30 km pendant la troisième heure de son parcours, avec une vitesse moyenne de 30 km/h.
f. Pendant la première heure, sa vitesse moyenne est 20 km/h.
Or 20 + 40 % × 20 = 20 + 8 = 28 et 30 > 28.
On peut donc affirmer que sa vitesse moyenne lors de la troisième heure est supérieure de plus de 40 % à sa vitesse moyenne lors de la première heure.
Or 20 + 40 % × 20 = 20 + 8 = 28 et 30 > 28.
On peut donc affirmer que sa vitesse moyenne lors de la troisième heure est supérieure de plus de 40 % à sa vitesse moyenne lors de la première heure.
g. Quentin a parcouru 95 km en 4,5 h.
Sa vitesse moyenne lors de cette sortie est donc :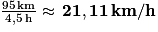 .
.
Sa vitesse moyenne lors de cette sortie est donc :
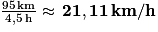 .
.Exercice 3
1.
On se reportera au document ressource des programmes « Espace et géométrie au cycle 3 - Les polygones », et notamment aux tableaux des pages 4, 5 et 6 sur les définitions et propriétés des quadrilatères.
Il est nécessaire avant de se présenter au CRPE de s'entraîner à la programmation, si possible avec Scratch en ligne, dont vous remarquez dans l'adresse qu'il a été développé par le MIT (pour les enfants).
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4
Avec ce script, on a dessiné un quadrilatère dont chaque côté mesure 100 pas et qui possède quatre angles droits.
Puisque ses quatre côtés ont la même longueur, ce quadrilatère est un losange.
Puisque ses quatre angles sont droits, ce quadrilatère est un rectangle.
Ce quadrilatère est un carré, puisque c'est à la fois un rectangle et un losange.
Par conséquent :
Puisque ses quatre côtés ont la même longueur, ce quadrilatère est un losange.
Puisque ses quatre angles sont droits, ce quadrilatère est un rectangle.
Ce quadrilatère est un carré, puisque c'est à la fois un rectangle et un losange.
Par conséquent :
• ce qu'affirme Pierre est vrai (position prototypique d'un losange) ;
• ce qu'affirme Ana est faux (elle ne voit pas les angles droits de ce rectangle qui n'est pas en position prototypique) ;
• ce qu'affirme Karim est vrai ;
• ce qu'affirme Lucie est vrai.
2.
GeoGebra est un logiciel de géométrie dynamique (que l'on peut utiliser en ligne https://www.geogebra.org/classic?lang fr). Il très utilisé en cycle 4 mais aussi en cycle 3 par les professeurs et leurs élèves.
Si vous débutez, vous pourrez consulter https://www.geogebra.org/m/cngmubdm, puis https://www.geogebra.org/m/fhtds8a2
Si vous débutez, vous pourrez consulter https://www.geogebra.org/m/cngmubdm, puis https://www.geogebra.org/m/fhtds8a2
a. On sait que la longueur d'un côté du pentagone obtenu est proportionnelle à la longueur du segment [RS] choisie au départ. On peut donc établir le tableau de proportionnalité suivant : 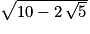
On en déduit que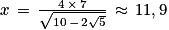 .
.
Si on veut obtenir un pentagone de 7 cm de côté, il faut commencer par un segment [RS] d'environ 11,9 cm.
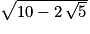
| Longueur du segment [RS] choisie au départ en cm | 4 | x |
| Longueur d'un côté du pentagone obtenu en cm | | 7 |
On en déduit que
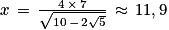 .
.Si on veut obtenir un pentagone de 7 cm de côté, il faut commencer par un segment [RS] d'environ 11,9 cm.
b.
En utilisant le programme de construction, on obtient la figure suivante, en reportant cinq fois la longueur LD au compas sur le cercle de diamètre [RS] (d'où les arcs de cercle) :
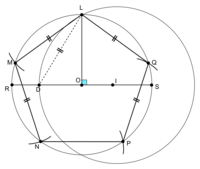 |
c.
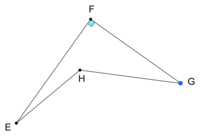
Dans la figure de l'énoncé, considérons le triangle FCG isocèle en C :
ses angles de base sont de même mesure, donc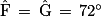 .
.
La somme des angles d'un triangle étant égale à 180°,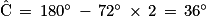 .
.
ses angles de base sont de même mesure, donc
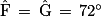 .
.La somme des angles d'un triangle étant égale à 180°,
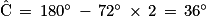 .
.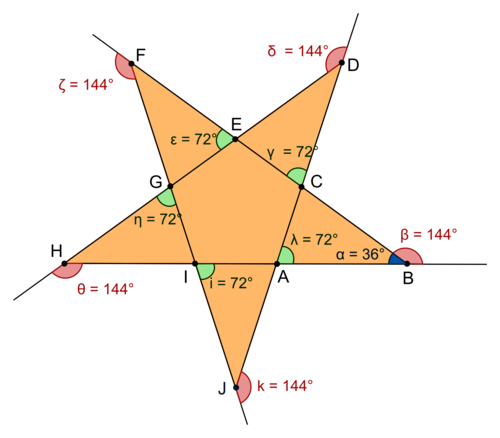 |
Soit A le point de départ de la construction de la figure :
Les sommets de la figure obtenue avec Scratch n'étant pas nommés, on peut saisir le script suivant :
Remarques :
- on trace un segment [AB] horizontal de longueur 80 pas ;
- puis on tourne de 180° − 36° = 144° dans le sens inverse des aiguilles d'une montre (angle codé en rouge sur la figure ci-dessus) ;
- on trace le segment [BC] de longueur 80 pas ;
- on tourne de 72° dans le sens des aiguilles d'une montre (angle codé en vert sur la figure ci-dessus) ;
- on trace le segment [CD] de longueur 80 pas, etc.
Les sommets de la figure obtenue avec Scratch n'étant pas nommés, on peut saisir le script suivant :
Remarques :
• Pour créer votre propre script, cliquez sur créer sur la page d'accueil.
• En cliquant en haut à gauche sur le globe, vous pouvez choisir le français.
• Pour obtenir les instructions avec le stylo, cliquez sur l'icône
 |
en bas à gauche de l'écran, puis choisissez comme extension stylo.
• Les couleurs vous permettront de gagner du temps pour repérer chaque instruction.
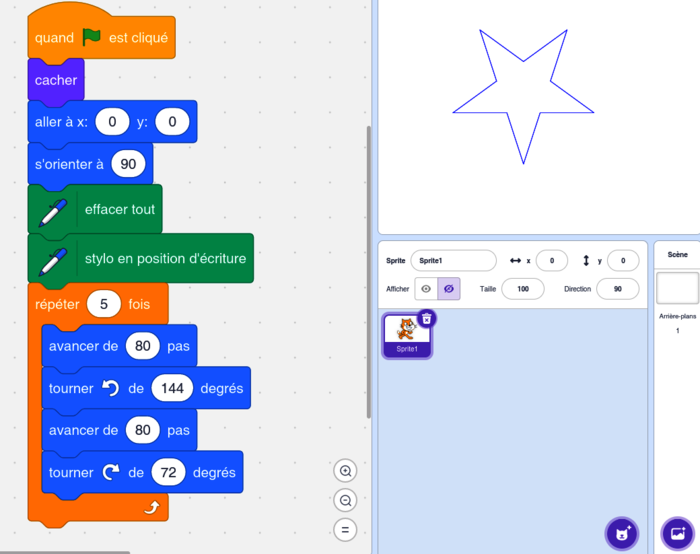 |
La ligne 7 comporte l'instruction : « répéter 5 fois ».
La ligne 9 comporte l'instruction : « tourner dans le sens inverse des aiguilles d'une montre de 144° ».
La ligne 9 comporte l'instruction : « tourner dans le sens inverse des aiguilles d'une montre de 144° ».
d. Cette étoile est délimitée par 10 segments de branches de 80 pas : son périmètre est donc égal à 80 pas × 10 =800 pas.
e. Si on veut agrandir cette étoile afin que son périmètre double, toutes les longueurs doivent doubler, donc les branches doivent mesurer 160 pas, à modifier dans les lignes 8 et 10. En revanche, les mesures des angles restent inchangées au cours d'un agrandissement, donc il n'y a pas de modification dans les lignes 9 et 11.
Exercice 4
1.
Un élève obtient 3 et 2 avec les dés, donc deux nombres différents. Il peut :
- soit passer son tour et ne prendre aucun jeton ;
- soit prendre 3 jetons ;
- soit prendre 2 × 2 = 4 jetons.
2.
Un tirage permet d'obtenir 3 jetons suivant l'un des cas suivants :
- les dés indiquent les nombres 2 et 3.
(Remarque : comme 3 est impair, 3 ne peut pas être le double du plus petit nombre).
- les deux dés indiquent le même nombre 3 ;
- le nombre 3 est le plus grand des deux nombres, donc
- les dés indiquent les nombres 2 et 3.
(Remarque : comme 3 est impair, 3 ne peut pas être le double du plus petit nombre).
3.
On peut considérer le lancer des deux dés et la donnée les deux nombres indiqués sur les faces supérieures de chacun des dés comme une expérience aléatoire de 6 × 6 = 36 issues équiprobables (que l'on trouve dans le tableau ci-dessous).
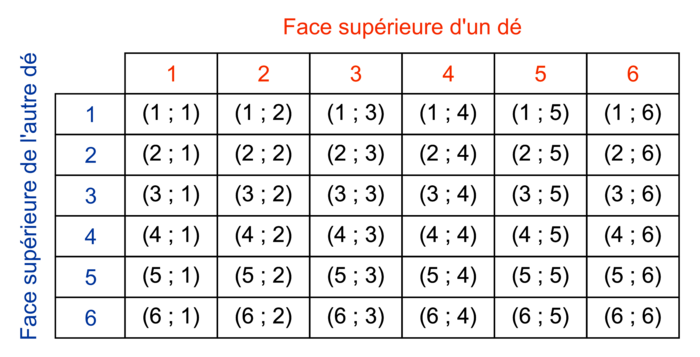 |
Si toutes les issues sont équiprobables, la probabilité d'un événement se calcule par :
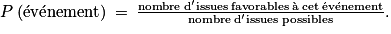
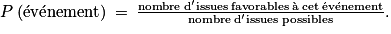
a. Obtenir un 3 et un 2 est un événement qui peut se produire avec l'une des issues suivantes :
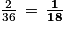 .
.
- soit le premier dé considéré indique 2 et l'autre dé indique 3 (issue (2 ; 3)) ;
- soit le premier dé considéré indique 3 et l'autre dé indique 2 (issue (3 ; 2)).
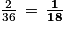 .
.b. On considère l'événement : « Au moins un des nombres obtenus est 3 ». Les 11 issues favorables sont (3 ; 1) − (3 ; 2) − (3 ; 3) − (3 ; 4) − (3 ; 5) − (3 ; 6) − (1 ; 3) − (2 ; 3) − (24 ; 3) − (5 ; 3) − (6 ; 3).
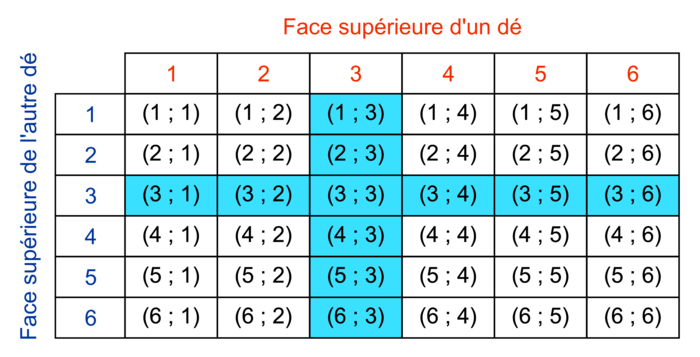 |
Par conséquent, la probabilité d'obtenir au moins un 3 est égale à 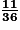 .
.
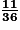 .
.c. Un tirage permet d'obtenir 4 jetons après l'un des lancers suivants :
- les deux dés indiquent le même nombre 4 (1 seule issue (4 ; 4)) ;
- le nombre 4 est le double du nombre le plus petit indiqué par les dés pour les 8 issues (2 ; 3) − (2 ; 4) − (2 ; 5) − (2 ; 6) − (3 ; 2) − (4 ; 2) − (5 ; 2) − (6 ; 2) ;
- le nombre 4 est le plus grand des deux nombres indiqués par le dé pour les 6 issues (1 ; 4) − (2 ; 4) − (3 ; 4) − (4 ; 1) − (4 ; 2) − (4 ; 3).
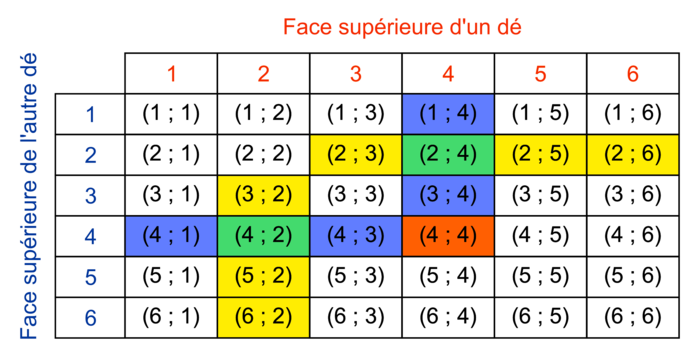 |
En remarquant que les issues (2 ; 4) et (4 ; 2) ne peuvent pas être comptées deux fois, il y a donc 1 + 4 + 6 + 2 = 13 issues distinctes favorables à l'événement : « Avoir un lancer permettant d'obtenir 4 jetons. » Donc la probabilité de cet événement est égale à 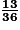 .
.
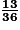 .
.4. Chaque lancer des deux dés est indépendant du précédent, donc la probabilité que le joueur prenne 3 jetons est identique à chaque lancer.
5. Le but du jeu est d'avoir exactement 15 jetons. Un élève qui en a déjà 12, lance le dé et obtient 1 et 4 ; il peut donc prendre :
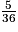 .
.
En passant son tour, il a une probabilité d'obtenir exactement 15 jetons au prochain tour 5 fois plus élevée que s'il prend 2 jetons (et s'il prend 4 jetons, il est certain de perdre) : c'est pourquoi il est préférable qu'il passe son tour.
- soit 4 jetons : il aurait alors trop de jetons et ne pourrait plus jamais n'en avoir que 15 ;
- soit 2 jetons (le double de 1) : il aurait alors 14 jetons et il lui manquerait 1 jeton. Or la seule issue favorable pour obtenir 1 (et 1 seul) jeton est (1 ; 1). Il n'a donc qu'une chance sur 36 à chaque tour suivant d'avoir exactement 1 jeton, probabilité assez faible ;
- ne prendre aucun jeton : il lui manquera 3 jetons qu'il peut espérer obtenir au prochain lancer avec les 5 issues (3 ; 1) − (3 ; 2) − (3 ; 3) − (1 ; 3) − (2 ; 3).
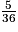 .
.En passant son tour, il a une probabilité d'obtenir exactement 15 jetons au prochain tour 5 fois plus élevée que s'il prend 2 jetons (et s'il prend 4 jetons, il est certain de perdre) : c'est pourquoi il est préférable qu'il passe son tour.
Exercice 5
On retrouvera les définitions des différents types de nombre sur le document ressource du programme de cycle 3 « Fractions et nombres décimaux au cycle 3 » à partir de la page 5 https://eduscol.education.fr/document/16510/download
1. L'affirmation 1 est vraie, car 257 est un entier et tout nombre entier est un nombre décimal.
2. 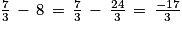 est un nombre rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers. L'affirmation 2 est vraie.
est un nombre rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers. L'affirmation 2 est vraie.
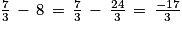 est un nombre rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers. L'affirmation 2 est vraie.
est un nombre rationnel, puisqu'il peut s'écrire sous la forme d'une fraction, c'est-à-dire d'un quotient de deux nombres entiers. L'affirmation 2 est vraie.3. Soit n un entier, n + 1 l'entier consécutif à n et n + 2 l'entier consécutif à n + 1. On note S la somme de ces trois nombres consécutifs :
S = n + (n + 1) + (n + 2)= 3n + 3 = 3(n + 1).
Comme est n + 1 est un entier, 3(n + 1) est l'écriture d'un multiple de 3, ce qui prouve que S est divisible par 3 : l'affirmation 3 est vraie.
S = n + (n + 1) + (n + 2)= 3n + 3 = 3(n + 1).
Comme est n + 1 est un entier, 3(n + 1) est l'écriture d'un multiple de 3, ce qui prouve que S est divisible par 3 : l'affirmation 3 est vraie.
4.
Résolvons l'équation donnée en commençant par développer les produits de chaque membre de l'égalité :
Quels que soient les nombres a, b, c et d :
(a + b)(c + d) = ac + ad + bc + bd
(a − b)(c + d) = ac + ad − bc − bd
(a + b)(c − d) = ac − ad + bc − bd
(a − b)(c − d) = ac − ad − bc + bd
(a + b)(c + d) = ac + ad + bc + bd
(a − b)(c + d) = ac + ad − bc − bd
(a + b)(c − d) = ac − ad + bc − bd
(a − b)(c − d) = ac − ad − bc + bd
(x + 1)(x − 2) = (x − 3)(x + 4)
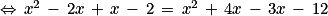
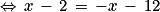
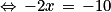
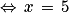
L'équation donnée a une seule solution, le nombre 5 qui est entier : l'affirmation 4 est vraie.
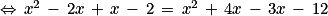
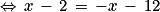
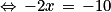
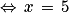
L'équation donnée a une seule solution, le nombre 5 qui est entier : l'affirmation 4 est vraie.
5.
On pourra consulter un cours de 3e sur les pourcentages, par exemple sur le site www.math93.com.
Augmenter de 15 % une quantité revient à la multiplier par 1 + 15 % = 1,15.
Augmenter de 10 % une quantité revient à la multiplier par 1 + 10 % = 1,1.
Augmenter une quantité de 15 % puis de 10 % revient à la multiplier par 1,15 × 1,1 = 1,265 = 1 + 26,5 %, donc à l'augmenter de 26,5 % et non de 25 %.
L'affirmation 5 est fausse.
Augmenter de 10 % une quantité revient à la multiplier par 1 + 10 % = 1,1.
Augmenter une quantité de 15 % puis de 10 % revient à la multiplier par 1,15 × 1,1 = 1,265 = 1 + 26,5 %, donc à l'augmenter de 26,5 % et non de 25 %.
L'affirmation 5 est fausse.
Autre procédure par la donnée d'un contre-exemple qui suffit à prouver qu'une affirmation est fausse
Soit une quantité Q = 100.
Si Q augmente de 15 %, alors devient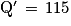 .
.
Si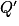 augmente de 10 %, alors
augmente de 10 %, alors 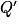 devient
devient 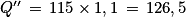 .
.
Or Q augmenté de son quart devient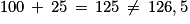 .
.
Ce contre-exemple montre que l'affirmation 5 est fausse.
Si Q augmente de 15 %, alors devient
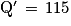 .
.Si
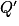 augmente de 10 %, alors
augmente de 10 %, alors 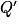 devient
devient 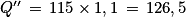 .
.Or Q augmenté de son quart devient
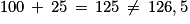 .
.Ce contre-exemple montre que l'affirmation 5 est fausse.
Attention : un exemple ou même un grand nombre d'exemples ne permettent pas de justifier qu'une affirmation est vraie.
6.
L'affirmation 6 est fausse, puisqu'il existe des quadrilatères possédant un angle droit qui ne sont pas des rectangles. Voici la représentation de deux contre-exemples :
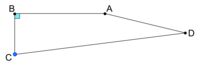 |
7. Un triangle rectangle a un angle droit qui mesure 90°.
 |
Chacun des angles d'un triangle équilatéral mesure 60°.
L'affirmation 7 est fausse : un triangle rectangle ne peut pas être équilatéral.
L'affirmation 7 est fausse : un triangle rectangle ne peut pas être équilatéral.
8. f(x) = −3x + 1.
Déterminons l'antécédent de 4 par la fonction affine f :
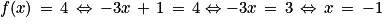
L'antécédent de 4 par la fonction affine f est le nombre −1, donc l'affirmation 8 est fausse.
Déterminons l'antécédent de 4 par la fonction affine f :
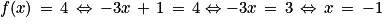
L'antécédent de 4 par la fonction affine f est le nombre −1, donc l'affirmation 8 est fausse.
9. Le plus grand côté du triangle ABC est [AC].
D'une part, AC2 = 392 = 1 521.
D'autre part, AB2 + BC2 = 352 + 122 = 1 225 + 144 = 1 369.
Puisque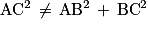 , le triangle ABC n'est pas rectangle, puisque s'il l'était, d'après le théorème de Pythagore, l'égalité serait vraie.
, le triangle ABC n'est pas rectangle, puisque s'il l'était, d'après le théorème de Pythagore, l'égalité serait vraie.
L'affirmation 9 est fausse.
Remarque : C'est la contraposée du théorème de Pythagore que l'on applique ici.
D'une part, AC2 = 392 = 1 521.
D'autre part, AB2 + BC2 = 352 + 122 = 1 225 + 144 = 1 369.
Puisque
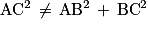 , le triangle ABC n'est pas rectangle, puisque s'il l'était, d'après le théorème de Pythagore, l'égalité serait vraie.
, le triangle ABC n'est pas rectangle, puisque s'il l'était, d'après le théorème de Pythagore, l'égalité serait vraie.L'affirmation 9 est fausse.
Remarque : C'est la contraposée du théorème de Pythagore que l'on applique ici.
10.
Lors d'un agrandissement ou d'une réduction :
- toutes les longueurs sont multipliées par un même nombre k, (k < 1 pour une réduction et k > 1 pour une augmentation) ;
- toutes les aires sont multipliées par k2 ;
- tous les volumes sont multipliés par k3.
L'agrandissement considéré est de coefficient k = 3, donc les aires sont multipliées par k2 = 9 et non par 3 : l'affirmation 10 est fausse.
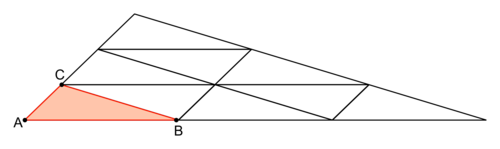
Remarque : Il faut 9 pièces identiques au triangle ABC pour construire un triangle « plein » trois fois plus grand que le triangle ABC.
Remarque : Il faut 9 pièces identiques au triangle ABC pour construire un triangle « plein » trois fois plus grand que le triangle ABC.
 |
Document précédent
Sujet 2023 de mathématiques, groupement académique 2
