Dernier essai le
- Score :
/20
Ce sujet est composé de six exercices indépendants.
EXERCICE 1
Un professeur des écoles organise avec sa classe de CM1 une randonnée à vélo. Le parcours BCEFCDB est représenté ci-dessous.
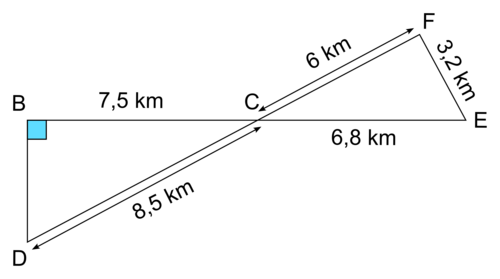 |
1. Montrer que l'angle 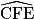 est droit.
est droit.
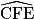 est droit.
est droit.2. Déterminer la longueur totale du parcours.
3. Sachant que la vitesse moyenne du groupe est 14 km/h, la classe fera-t-elle le parcours en moins de 2 h 45 min ? Justifier la réponse.
EXERCICE 2
1.
Quatre personnes A, B, C, D se partagent une somme d'argent. On appelle a, b, c et d les montants respectivement reçus par A, B, C et D. On sait par ailleurs que :
• a représente 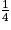 de la somme totale ;
de la somme totale ;
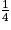 de la somme totale ;
de la somme totale ;• b représente 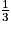 de la somme totale ;
de la somme totale ;
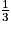 de la somme totale ;
de la somme totale ;• C et D se partagent ce qui reste en prenant chacun le même montant.
a. Déterminer la proportion que représente c par rapport à la somme totale.
b. D reçoit 55 €. Déterminer les valeurs de a, b et c.
2.
Quatre personnes E, F, G, H se partagent une somme d'argent s. On appelle e, f, g et h les montants respectivement reçus par E, F, G et H. On sait par ailleurs que :
• E perçoit le triple de F ;
• g + h représente 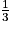 de la somme totale ;
de la somme totale ;
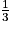 de la somme totale ;
de la somme totale ;• g = h.
Exprimer la part de chacun en fonction de s.
EXERCICE 3
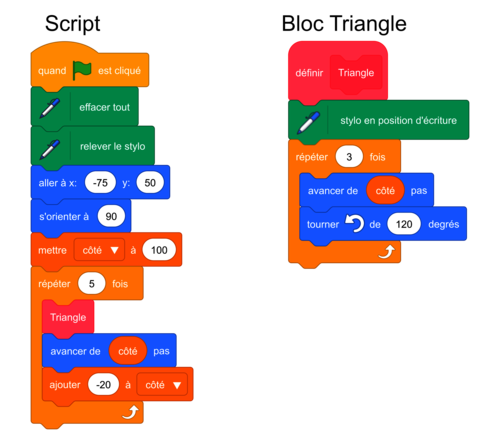
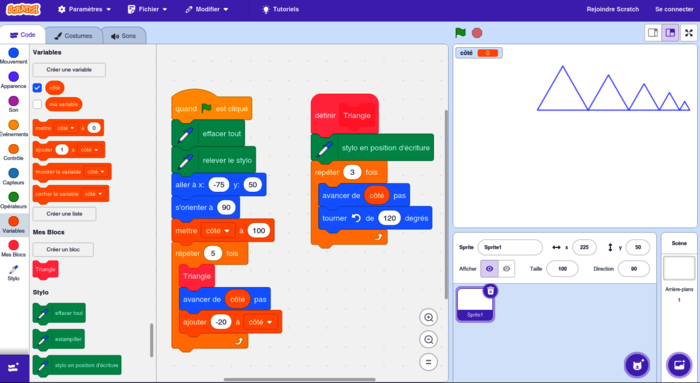
On donne le programme ci-dessous qui permet de tracer des triangles de tailles différentes.
Ce programme comporte une variable nommée « côté ». Les longueurs sont données en pixels.
Ce programme comporte une variable nommée « côté ». Les longueurs sont données en pixels.
 |
On rappelle que l'instruction
 |
signifie que l'on se dirige vers la droite.
1.
Répondre aux questions suivantes sans justifier.
L'utilisateur clique sur le drapeau.
L'utilisateur clique sur le drapeau.
a. Quelles sont les coordonnées du point de départ du tracé ?
b. Combien de triangles sont dessinés par le script ?
c. Quelle est la nature des triangles dessinés ?
d. Quelle est la longueur (en pas) d'un côté du deuxième triangle tracé ?
2. Tracer le dessin obtenu par ce programme en prenant comme échelle 1 cm pour 20 pas.
3. Si au lieu de triangles on voulait obtenir des hexagones réguliers, que devrait-on changer dans les instructions du bloc triangle ?
EXERCICE 4
Partie A
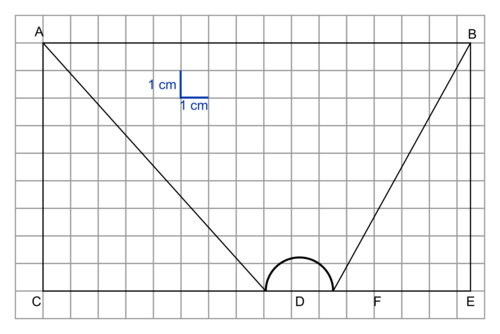
Dans une école, un jardin pédagogique est constitué d'un terrain rectangulaire ABEC dont l'aire est égale à 100 m2.
Des enseignants de l'école décident de planter avec les élèves différentes cultures sur ce terrain : des fraisiers, des pieds de tomates et des radis.
La répartition dans le terrain est la suivante :
Des enseignants de l'école décident de planter avec les élèves différentes cultures sur ce terrain : des fraisiers, des pieds de tomates et des radis.
La répartition dans le terrain est la suivante :
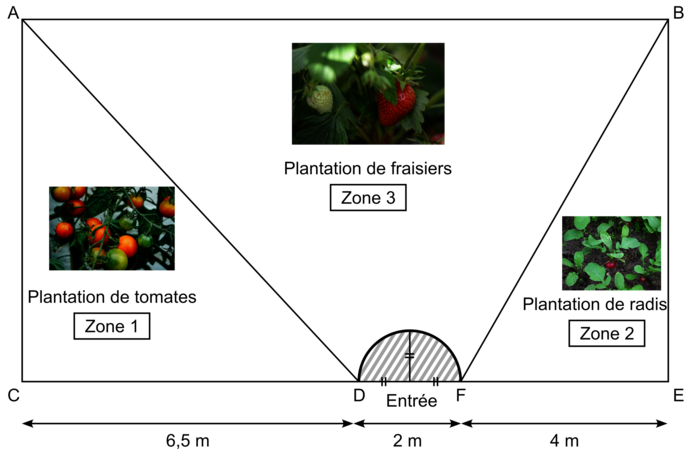 |
L'entrée est un demi-disque délimité par le demi-cercle de diamètre [DF] (zone hachurée sur la figure ci-dessus). Elle doit rester libre de toute plantation.
1. Justifier que la largeur du terrain correspondant au segment [CA] est égale à 8 m.
2. Tracer un plan du terrain avec les différentes zones à l'échelle 1: 80.
3.
Le directeur de l'école veut installer une bordure sur les trois côtés autour de la zone 1 où on plante des tomates.
a. Montrer que 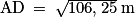 .
.
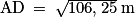 .
.b. Déterminer la longueur de la bordure qu'il doit acheter. On donnera le résultat en mètres, arrondi à l'unité.
c. Les bordures sont vendues par rouleaux de 4 mètres. Déterminer le nombre de rouleaux nécessaires pour entourer la zone 1.
4.
On veut déterminer l'aire de chacune des zones.
a. Calculer l'aire de la zone 1, en mètres carrés.
b. Calculer l'aire de la zone 2, où on plante des radis, en mètres carrés.
c. En déduire l'aire de la zone 3, où on plante des fraisiers (sans la zone « Entrée » hachurée sur la figure), en mètres carrés. Donner la valeur exacte puis la valeur arrondie au dixième.
5. On s'intéresse à la culture des fraisiers.
Sachant que l'on peut planter 6 pieds de fraisiers par m2 et qu'un pied de fraisier produit en moyenne 650 grammes de fraises par année, quelle masse de fraises les élèves peuvent-ils espérer récolter ? On donnera le résultat en kilogrammes, arrondi à l'unité.
Sachant que l'on peut planter 6 pieds de fraisiers par m2 et qu'un pied de fraisier produit en moyenne 650 grammes de fraises par année, quelle masse de fraises les élèves peuvent-ils espérer récolter ? On donnera le résultat en kilogrammes, arrondi à l'unité.
Partie B
Fin juin, l'école décide de récolter des fraises pour faire de la confiture. Les élèves récoltent ainsi 25 kg de fraises.
1. La recette de confiture de fraises dit que la quantité de sucre nécessaire doit correspondre à 55 % de la masse totale avant cuisson. Quelle masse de sucre, arrondie au kilogramme, le directeur doit-il acheter pour respecter cette recette ?
2. Sachant que 3 kg de fraises permettent de réaliser 4,8 L de confiture, combien de litres de confiture peut-on réaliser ?
3. Il décide de conditionner cette confiture dans des pots cylindriques dont la base est un disque de diamètre 8,4 cm et dont la hauteur mesure 11 cm.
Sachant que les pots ne peuvent être remplis qu'aux 8/9 de leur capacité maximale, déterminer le nombre de pots de confiture qu'il devrait réaliser.
Sachant que les pots ne peuvent être remplis qu'aux 8/9 de leur capacité maximale, déterminer le nombre de pots de confiture qu'il devrait réaliser.
On rappelle la formule suivante : Volume d'un prisme ou d'un cylindre : V = B × h, où B désigne l'aire de la base du prisme ou du cylindre, et h sa hauteur.
EXERCICE 5
Un enseignant souhaite décorer sa salle de classe avec une frise chronologique allant de la chute de l'Empire romain (476) à nos jours. Cette frise devra couvrir trois murs de la salle de classe rectangulaire en commençant par le coin nord-ouest et en tournant dans le sens des aiguilles d'une montre. La frise passe au-dessus de la porte et s'étend ainsi sur les murs nord, est et sud.
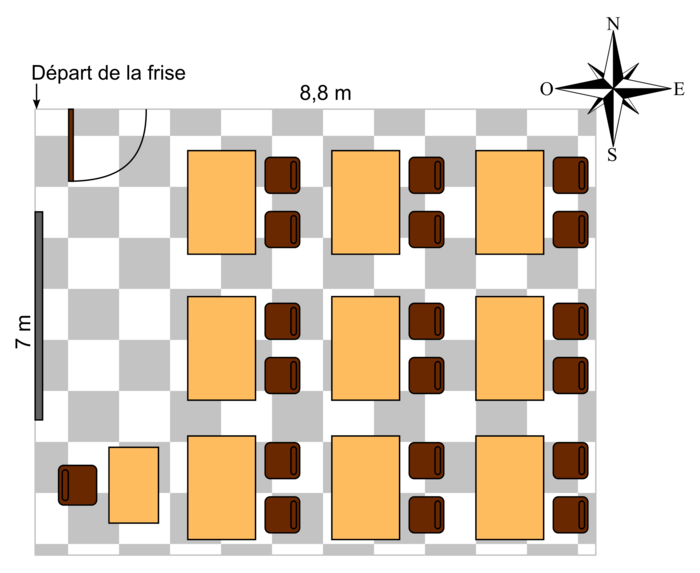 |
1. Pour effectuer cette frise, l'enseignant prévoit d'assembler bord à bord des feuilles de format A4 (21 × 29,7 cm) dans le sens de la longueur.
Montrer qu'il faudra 83 feuilles pour réaliser la frise.
Montrer qu'il faudra 83 feuilles pour réaliser la frise.
2. Par combien de centimètres est représentée une année sur cette frise chronologique ? Arrondir au millimètre près.
3.
L'enseignant a répertorié dans une feuille de calcul automatisé des dates importantes qu'il aimerait faire figurer sur cette frise.
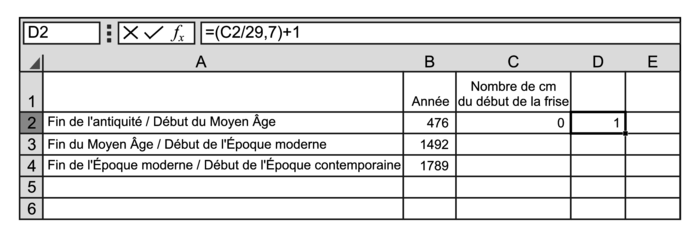 |
a. Proposer une formule à valider dans la cellule C2, pouvant être étirée vers le bas afin de trouver tous les résultats de la colonne C.
b. Sachant que la formule validée dans la cellule D2 est « = ENT(C2/29,7) + 1 », déterminer à quoi correspondent les nombres de la colonne D au sein de la salle de classe.
On rappelle que « ENT(x) » renvoie la partie entière du nombre x.
On rappelle que « ENT(x) » renvoie la partie entière du nombre x.
4. Sur quel mur de la classe se trouvera l'événement « l'accostage de Christophe Colomb sur le continent américain », marquant la fin du Moyen Âge, si on le positionne sur la frise ?
EXERCICE 6
Dans une école élémentaire de 150 élèves, 80 sont des filles. Le directeur veut mettre en place un « orchestre à l'école ». Il réalise une enquête auprès des familles de l'école afin de connaître les élèves qui pratiquent déjà un instrument de musique.
À l'issue de l'enquête, il apparaît que 24 % des élèves sont musiciens.
Parmi ces élèves, 16 sont des garçons.
À l'issue de l'enquête, il apparaît que 24 % des élèves sont musiciens.
Parmi ces élèves, 16 sont des garçons.
1. Reproduire et compléter le tableau suivant.
| | Nombre d'élèves musiciens | Nombre d'élèves non musiciens | Total |
| Nombre de filles | | | |
| Nombre de garçons | | | |
| Total | | | 150 |
2.
Dans cette question, on écrira les résultats sous forme de fractions irréductibles.
On interroge un élève au hasard.
On interroge un élève au hasard.
a. Quelle est la probabilité que ce soit un garçon ?
b. Quelle est la probabilité que ce soit une fille musicienne ?
c. Quelle est la probabilité que ce soit un élève non musicien ?
3. L'élève interrogé est un garçon. Quelle est la probabilité qu'il soit musicien ?
4. 30 % des filles musiciennes jouent d'un instrument à vent. Quel pourcentage cela représente-t-il par rapport à l'effectif total de l'école ?
Corrigé
Corrigé
Exercice 1
1.
Pour montrer que l'angle 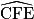 est droit, on va appliquer la propriété (ou théorème) réciproque de Pythagore au triangle CFE.
est droit, on va appliquer la propriété (ou théorème) réciproque de Pythagore au triangle CFE.
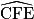 est droit, on va appliquer la propriété (ou théorème) réciproque de Pythagore au triangle CFE.
est droit, on va appliquer la propriété (ou théorème) réciproque de Pythagore au triangle CFE.Propriété réciproque de Pythagore (permettant de montrer qu'un triangle, dont on connaît la longueur des trois côtés, est rectangle) :
Si le carré de la longueur du plus long côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et son plus grand côté est l'hypoténuse.
Si le carré de la longueur du plus long côté est égal à la somme des carrés des longueurs des deux autres côtés, alors ce triangle est rectangle et son plus grand côté est l'hypoténuse.
Dans le triangle CFE, le plus long côté est [CE].
D'une part, CE2 = 6,8 km2 = 46,24 km2.
D'autre part, CF2 + FE2 = 62 km2 + 3,22 km2 = 36 km2 + 10,24 km2 = 46,24 km2.
Puisque CE2 = CF2 + FE2, on en déduit, d'après la propriété réciproque de Pythagore, que le triangle CFE est rectangle en F, donc que l'angle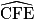 est droit.
est droit.
D'une part, CE2 = 6,8 km2 = 46,24 km2.
D'autre part, CF2 + FE2 = 62 km2 + 3,22 km2 = 36 km2 + 10,24 km2 = 46,24 km2.
Puisque CE2 = CF2 + FE2, on en déduit, d'après la propriété réciproque de Pythagore, que le triangle CFE est rectangle en F, donc que l'angle
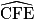 est droit.
est droit.2.
D'après le codage de la figure, le triangle BCD est rectangle en B. Pour calculer la longueur du côté [BD], on va appliquer la propriété de Pythagore à ce triangle.
Propriété de Pythagore (permettant de calculer la longueur d'un côté d'un triangle rectangle quand on connaît la longueur de ses deux autres côtés).
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Si un triangle est rectangle, alors le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Le triangle BCD étant rectangle en B, d'après la propriété de Pythagore, on a :
CD2 = CB2 + BD2.
On en déduit :
BD2 = CD2 − CB2 = 8,52 km2 − 7,52 km2 = 72,25 km2 − 56,25 km2 = 16 km2.
BD = 4 km.
On peut à présent calculer la longueur du parcours :
BC + CE + EF + FC + CD + DB
= 7,5 km + 6,8 km + 3,2 km + 6 km + 8,5 km + 4 km = 36 km.
CD2 = CB2 + BD2.
On en déduit :
BD2 = CD2 − CB2 = 8,52 km2 − 7,52 km2 = 72,25 km2 − 56,25 km2 = 16 km2.
BD = 4 km.
On peut à présent calculer la longueur du parcours :
BC + CE + EF + FC + CD + DB
= 7,5 km + 6,8 km + 3,2 km + 6 km + 8,5 km + 4 km = 36 km.
3.
La vitesse moyenne est 14 km/h sur un parcours de 36 km.
Procédure basée sur le calcul mental et les propriétés additives et multiplicatives de la linéarité
Procédure basée sur le calcul mental et les propriétés additives et multiplicatives de la linéarité
On consultera le document ressource « Résoudre des problèmes de proportionnalité au cycle 3 » sur https://eduscol.education.fr/document/16522/download
En 1 heure, la classe parcourt en moyenne 14 km.
En 2 heures, elle parcourt le double, soit 28 km.
En une demi-heure, elle parcourt moitié moins qu'en 1 heure, soit 7 km.
En un quart d'heure, elle parcourt une distance moitié moins grande qu'en une demi-heure, soit 3,5 km.
En 2 h 45 min, elle parcourt donc 28 km + 7 km + 3,5 km = 38,5 km, soit plus que la longueur du parcours. Donc elle parcourt tout le parcours de 36 km en moins de 2 h 45 min.
Autre procédure (moins pertinente dans ce cas !)
En 2 heures, elle parcourt le double, soit 28 km.
En une demi-heure, elle parcourt moitié moins qu'en 1 heure, soit 7 km.
En un quart d'heure, elle parcourt une distance moitié moins grande qu'en une demi-heure, soit 3,5 km.
En 2 h 45 min, elle parcourt donc 28 km + 7 km + 3,5 km = 38,5 km, soit plus que la longueur du parcours. Donc elle parcourt tout le parcours de 36 km en moins de 2 h 45 min.
Autre procédure (moins pertinente dans ce cas !)
Soit v la vitesse moyenne (non nulle) exprimée en km/h pour parcourir une distance d exprimée en km en un temps t (non nul) exprimé en heures, alors :
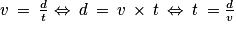
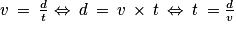
Le temps moyen t pour parcourir cette distance est donc égal à :
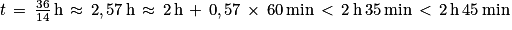 .
.
La classe fera donc le parcours en moins de 2 heures 45 min.
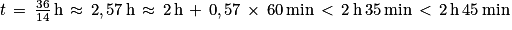 .
.La classe fera donc le parcours en moins de 2 heures 45 min.
Exercice 2
La schématisation n'est pas obligatoire pour un étudiant présentant ce concours, mais elle est vivement recommandée dans l'apprentissage de la résolution des problèmes dans l'enseignement primaire. On consultera le document « La résolution de problèmes mathématiques au cours moyen» sur https://eduscol.education.fr/document/32206/download?attachment, notamment page 126 « Focus | Exemples de résolution de problèmes de cours moyen avec des fractions en utilisant des schémas en barres ».
1.
Voici une schématisation pour mieux se représenter les données du problème.
La somme totale est schématisée par un rectangle que l'on peut partager équitablement en quatre :
La somme totale est schématisée par un rectangle que l'on peut partager équitablement en quatre :
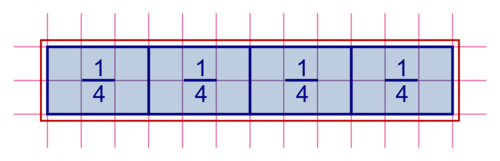 |
La somme totale est schématisée par le même rectangle que l'on peut aussi partager équitablement en trois, de cette façon :
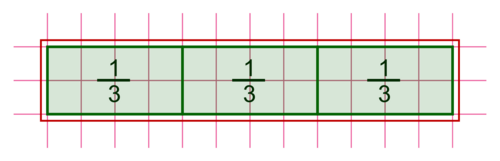 |
Le problème peut se schématiser ainsi :
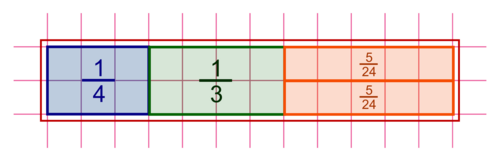 |
Procédure arithmétique
a. La personne A reçoit 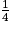 de la somme totale, et la personne B reçoit
de la somme totale, et la personne B reçoit 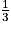 de la somme totale.
de la somme totale.
Les personnes A et B reçoivent à elles deux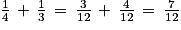 de la somme totale.
de la somme totale.
Il reste donc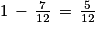 de cette somme, que se partagent équitablement C et D.
de cette somme, que se partagent équitablement C et D.
Par conséquent, C reçoit la moitié de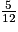 de la somme totale, soit
de la somme totale, soit 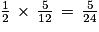 de la somme totale. Donc c représente
de la somme totale. Donc c représente 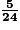 de la somme totale.
de la somme totale.
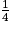 de la somme totale, et la personne B reçoit
de la somme totale, et la personne B reçoit 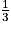 de la somme totale.
de la somme totale.Les personnes A et B reçoivent à elles deux
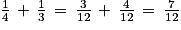 de la somme totale.
de la somme totale.Il reste donc
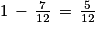 de cette somme, que se partagent équitablement C et D.
de cette somme, que se partagent équitablement C et D.Par conséquent, C reçoit la moitié de
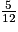 de la somme totale, soit
de la somme totale, soit 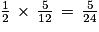 de la somme totale. Donc c représente
de la somme totale. Donc c représente 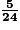 de la somme totale.
de la somme totale.b. D reçoit 55 €, donc C reçoit également 55 €.
Ces 55 € représentent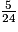 de la somme totale, donc 11 € (cinq fois moins que 55 €) représentent
de la somme totale, donc 11 € (cinq fois moins que 55 €) représentent 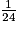 de la somme totale.
de la somme totale.
La somme totale est donc égale à 11 € × 24 = 264 €.
A reçoit donc 264 € ÷ 4 = 66 €, et B reçoit 264 € ÷ 3 = 88 €.
On en conclut que a = 66 €, b = 88 € et c = d = 55 €.
Ces 55 € représentent
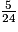 de la somme totale, donc 11 € (cinq fois moins que 55 €) représentent
de la somme totale, donc 11 € (cinq fois moins que 55 €) représentent 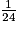 de la somme totale.
de la somme totale.La somme totale est donc égale à 11 € × 24 = 264 €.
A reçoit donc 264 € ÷ 4 = 66 €, et B reçoit 264 € ÷ 3 = 88 €.
On en conclut que a = 66 €, b = 88 € et c = d = 55 €.
Procédure algébrique
a. Soit s la somme totale que les quatre personnes se partagent.
D'après l'énoncé :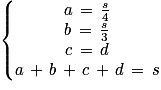
En substituant dans la dernière égalité a par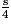 , b par
, b par 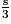 et c + d par 2c, on obtient :
et c + d par 2c, on obtient :
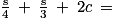
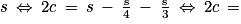
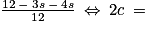
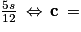
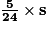 .
.
D'après l'énoncé :
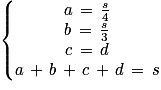
En substituant dans la dernière égalité a par
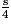 , b par
, b par 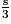 et c + d par 2c, on obtient :
et c + d par 2c, on obtient :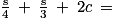
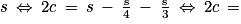
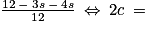
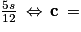
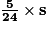 .
.b. 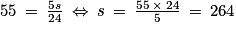 .
.
On en déduit que a = 264 ÷ 4 = 66, et b = 264 ÷ 3 = 88.
On vérifie que 66 + 88 + 2 × 55 = 264.
On en conclut que a = 66 €, b = 88 € et c = d = 55€.
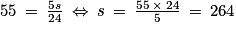 .
.On en déduit que a = 264 ÷ 4 = 66, et b = 264 ÷ 3 = 88.
On vérifie que 66 + 88 + 2 × 55 = 264.
On en conclut que a = 66 €, b = 88 € et c = d = 55€.
2. Procédure arithmétique avec schématisation
Nous allons représenter la somme totale s par un rectangle.
On sait que G et H perçoivent la même somme, et qu'à eux deux, ils perçoivent un tiers de s : on en conclut que chacun d'eux perçoit la moitié d'un tiers de s, soit un sixième de s (puisque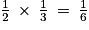 )
)
On partage donc équitablement la surface du rectangle en 6.
Nous allons représenter la somme totale s par un rectangle.
On sait que G et H perçoivent la même somme, et qu'à eux deux, ils perçoivent un tiers de s : on en conclut que chacun d'eux perçoit la moitié d'un tiers de s, soit un sixième de s (puisque
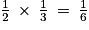 )
)On partage donc équitablement la surface du rectangle en 6.
 |
G et H ayant perçu ensemble deux sixièmes de s, il reste quatre sixièmes de s pour E et F : sachant que E perçoit le triple de F, F perçoit un sixième de s et E perçoit trois sixièmes de s, soit la moitié de s.
Conclusion : G, H et F perçoivent chacun un sixième de s, et E perçoit la moitié de s.
Procédure algébrique
Les données du problème peuvent se traduire par le système d'équations :
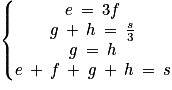
Puisque g = h, on substitue g par h dans la deuxième égalité :
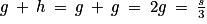 , d'où
, d'où 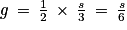 ; on en déduit que
; on en déduit que 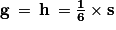 .
.
Dans la dernière égalité, on substitue e + f par 4f puisque e = 3f et on substitue g + h par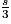 .
.
On obtient :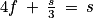 d'où
d'où 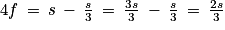 puis
puis 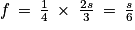 .
.
Par conséquent,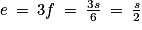 .
.
Conclusion :
Conclusion : G, H et F perçoivent chacun un sixième de s, et E perçoit la moitié de s.
Procédure algébrique
Les données du problème peuvent se traduire par le système d'équations :
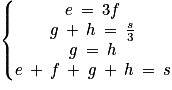
Puisque g = h, on substitue g par h dans la deuxième égalité :
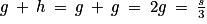 , d'où
, d'où 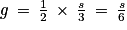 ; on en déduit que
; on en déduit que 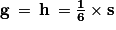 .
.Dans la dernière égalité, on substitue e + f par 4f puisque e = 3f et on substitue g + h par
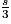 .
.On obtient :
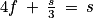 d'où
d'où 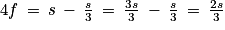 puis
puis 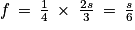 .
.Par conséquent,
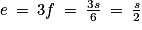 .
.Conclusion :
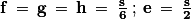 . . |
Exercice 3
Il est nécessaire avant de se présenter au CRPE de s'entraîner à la programmation, si possible avec Scratch (en ligne https://scratch.mit.edu/download/scratch2) dont vous remarquez dans l'adresse qu'il a été développé par le MIT (pour les enfants).
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4 https://eduscol.education.fr/document/17311/download
On pourra consulter le document ressource « Algorithme et programmation » des programmes du cycle 4 https://eduscol.education.fr/document/17311/download
Remarques :
• Pour créer votre propre script, cliquez sur créer sur la page d'accueil.
• En cliquant en haut à gauche sur le globe, vous pouvez choisir le français.
• Pour obtenir les instructions avec le stylo, cliquez sur l'icône
 |
en bas à gauche de l'écran, puis choisissez comme extension « stylo ».
• Si vous souhaitez écrire ce script, vous devrez créer une variable « côté » et un bloc triangle.
• Les couleurs vont permettront de gagner du temps pour repérer chaque instruction.
 |
1.
(Les justifications n'étaient pas demandées.)
a. Les coordonnées du point de départ du tracé sont (−75 ; 50), comme indiqué dans le script
 |
b. 5 triangles sont dessinés par le script, comme indiqué dans la boucle « Répéter 5 fois, triangle »
 |
c. Les triangles dessinés sont équilatéraux, puisque leurs trois côtés ont la même longueur (égale à la valeur de la variable « côté », constante dans le bloc).
d. Lors du tracé du premier triangle, la valeur de la variable « côté » est 100 pixels, puis la variable « côté » est augmentée de − 20, c'est-à-dire diminuée de 20 pixels. Elle est donc égale à 80 pixels lors du tracé du deuxième triangle.
2. Figure
Puisque l'on choisit pour échelle 1 cm pour 20 pas, 100 pas = 5 × 20 pas sont représentés par 5 cm qui est la longueur des côtés du premier triangle équilatéral tracé.
Pour chaque triangle tracé suivant, la longueur des côtés diminue de 20 pas, donc de 1 cm.
Puisque l'on choisit pour échelle 1 cm pour 20 pas, 100 pas = 5 × 20 pas sont représentés par 5 cm qui est la longueur des côtés du premier triangle équilatéral tracé.
Pour chaque triangle tracé suivant, la longueur des côtés diminue de 20 pas, donc de 1 cm.
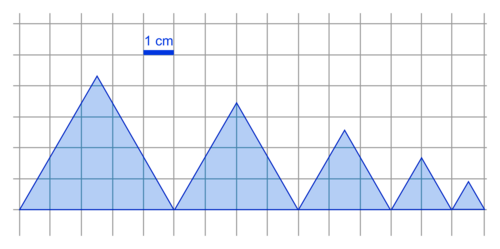 |
3.
Il conviendrait de tourner 6 fois (et non 3 fois) de 60° (et non de 120°) dans le bloc « hexagone » (qui remplacerait le bloc « triangle »).
Remarques hors sujet :
Remarques hors sujet :
• Afin d'éviter que les hexagones ne se coupent, il faut se déplacer de c + (c − 20) = 2c − 20 avant de débuter l'hexagone de côté c − 20 lorsqu'on a fini de tracer l'hexagone de côté c.
• Pour que les cinq hexagones juxtaposés réguliers soient tracés à l'intérieur du cadre, les coordonnées du point de départ et la longueur des côtés du premier hexagone doivent être modifiées.
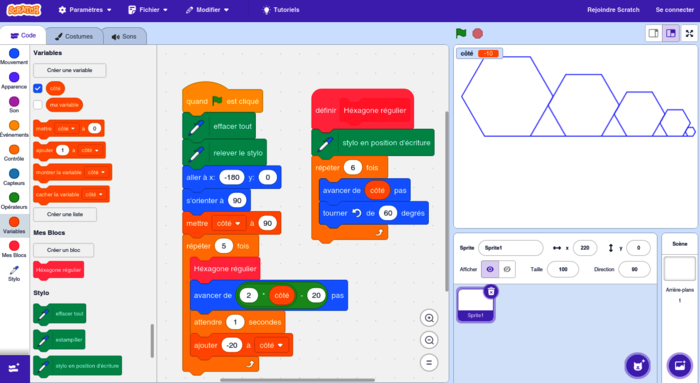 |
Exercice 4
Partie A
1. L'aire du rectangle est égale à 100 m2.
La longueur CE du rectangle est 6,5 m + 2 m + 4 m = 12,5 m.
On sait que l'aire d'un rectangle est égale au produit de sa longueur par sa largeur ; par conséquent, la largeur CA du rectangle est égale à 100 m2 ÷ 12,5 m = 8 m.
La longueur CE du rectangle est 6,5 m + 2 m + 4 m = 12,5 m.
On sait que l'aire d'un rectangle est égale au produit de sa longueur par sa largeur ; par conséquent, la largeur CA du rectangle est égale à 100 m2 ÷ 12,5 m = 8 m.
2.
Dans un plan à l'échelle 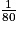 , les longueurs réelles sont réduites 80 fois.
, les longueurs réelles sont réduites 80 fois.
Par exemple, la largeur réelle du rectangle 8 m = 8 × 100 cm = 800 cm est représentée sur le plan par un segment de longueur 800 cm ÷ 80 = 10 cm.
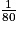 , les longueurs réelles sont réduites 80 fois.
, les longueurs réelles sont réduites 80 fois.Par exemple, la largeur réelle du rectangle 8 m = 8 × 100 cm = 800 cm est représentée sur le plan par un segment de longueur 800 cm ÷ 80 = 10 cm.
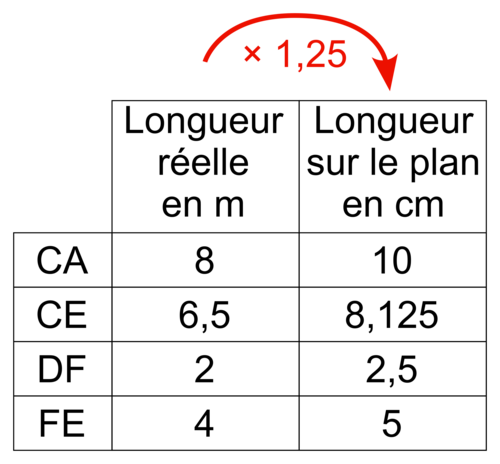
On peut donc multiplier par 100 les longueurs réelles en mètres pour les convertir en cm, puis les diviser par 80 pour obtenir les longueurs sur le plan, ce qui revient à les multiplier par 100 ÷ 80 = 1,25.
 |
 |
3.
a. On applique la propriété de Pythagore au triangle ACD rectangle en C :
AD2 = AC2 + CD2.
On en déduit : AD2 = 82 + 6,52 = 64 + 42,25 = 106,25, puis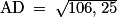 .
.
AD a pour longueur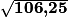 mètres.
mètres.
AD2 = AC2 + CD2.
On en déduit : AD2 = 82 + 6,52 = 64 + 42,25 = 106,25, puis
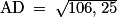 .
.AD a pour longueur
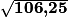 mètres.
mètres.b. La longueur de la bordure de la zone 1 est :
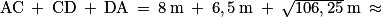 25 m .
25 m .
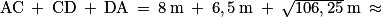 25 m .
25 m .c. 25m = 6 × 4 m + 1 m, d'après l'égalité caractéristique de la division euclidienne.
Il est donc nécessaire d'acheter 7 rouleaux de 4 m pour entourer la zone 1 (il manquerait 1 m si on n'achetait que 6 rouleaux).
Il est donc nécessaire d'acheter 7 rouleaux de 4 m pour entourer la zone 1 (il manquerait 1 m si on n'achetait que 6 rouleaux).
4.
Calcul de l'aire de chaque zone.
a. La zone 1 est délimitée par le triangle ACD rectangle en C, d'aire
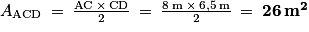 .
.
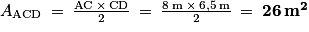 .
.b. La zone 2 est délimitée par le triangle EFB rectangle en E, d'aire
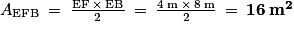 .
.
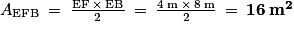 .
.c.
Soient AABFD l'aire du quadrilatère ABFD et AABEC l'aire du rectangle ABEC.
AABFD = AABEC − (AACD + AEFB) = 100 m2 − 42 m2 = 58 m2.
Pour calculer l'aire de la zone 3, il faut ôter l'aire du demi-disque de diamètre DF = 2 m, donc de rayon 1 m, à l'aire du quadrilatère ABFD.
AABFD = AABEC − (AACD + AEFB) = 100 m2 − 42 m2 = 58 m2.
Pour calculer l'aire de la zone 3, il faut ôter l'aire du demi-disque de diamètre DF = 2 m, donc de rayon 1 m, à l'aire du quadrilatère ABFD.
Aire d'un disque de rayon r = Π × r2.
On en déduit que l'aire du demi-disque de diamètre DF est égale à :
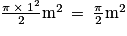 .
.
On en conclut que l'aire de la zone 3 est égale à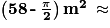 56m2.
56m2.
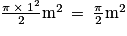 .
.On en conclut que l'aire de la zone 3 est égale à
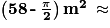 56m2.
56m2.5. La plantation des fraisiers est dans la zone 3.
La masse en kg de fraises espérée est égale à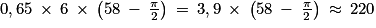 .
.
On peut espérer 220 kg de fraises.
La masse en kg de fraises espérée est égale à
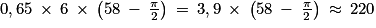 .
.On peut espérer 220 kg de fraises.
Partie B
On consultera à nouveau le document ressource « Résoudre des problèmes de proportionnalité au cycle 3 » sur https://eduscol.education.fr/document/16522/download
1. La masse du sucre correspond à 55 % de la masse totale avant cuisson : par conséquent, la masse de fraises correspond à 100 % − 55 % = 45 % de la masse totale avant cuisson.
Les 25 kg de fraises correspondent à 45 % de la masse totale avant cuisson,
Donc 1 % de la masse totale avant cuisson est égale à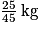 .
.
Et 55 % de la masse totale en kg avant cuisson est égale à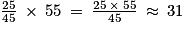 . Il faut donc acheter environ 31 kg de sucre.
. Il faut donc acheter environ 31 kg de sucre.
Les 25 kg de fraises correspondent à 45 % de la masse totale avant cuisson,
Donc 1 % de la masse totale avant cuisson est égale à
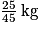 .
.Et 55 % de la masse totale en kg avant cuisson est égale à
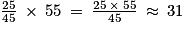 . Il faut donc acheter environ 31 kg de sucre.
. Il faut donc acheter environ 31 kg de sucre.2.
Le volume de confiture obtenue est proportionnel à la masse de fraises cuites pour la réaliser.
On sait qu'avec 3 kg de fraises, on obtient 4,8 L de confiture, donc par la méthode dite du produit en croix, avec 25 kg de fraises, on obtient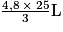 = 40 L de confiture.
= 40 L de confiture.
On sait qu'avec 3 kg de fraises, on obtient 4,8 L de confiture, donc par la méthode dite du produit en croix, avec 25 kg de fraises, on obtient
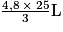 = 40 L de confiture.
= 40 L de confiture.Remarque : La méthode du « produit en croix » n'est pas au programme dans l'enseignement primaire, classes dans lesquelles il sera non aisé pour un(e) PE de donner du sens au produit que l'on effectue en 1er.
En CM1 et CM2, on résoudra le problème par la « règle de trois », c'est-à-dire le retour explicite à l'unité.
Avec 3 kg de fraises, on obtient 4,8 L de confiture ;
avec 1 kg de fraises, on obtient 3 fois moins de confiture qu'avec 3 kg de fraises, donc 4,8 L ÷ 3 = 1,6 L ;
avec 25 kg de fraises, on obtient 25 fois plus de confiture qu'avec 1 kg de fraises, donc 25 × 1,6 L = 40 L.
En CM1 et CM2, on résoudra le problème par la « règle de trois », c'est-à-dire le retour explicite à l'unité.
Avec 3 kg de fraises, on obtient 4,8 L de confiture ;
avec 1 kg de fraises, on obtient 3 fois moins de confiture qu'avec 3 kg de fraises, donc 4,8 L ÷ 3 = 1,6 L ;
avec 25 kg de fraises, on obtient 25 fois plus de confiture qu'avec 1 kg de fraises, donc 25 × 1,6 L = 40 L.
3.
Chaque pot de confiture est un cylindre dont la base a un rayon de 8,4 cm ÷ 2 = 4,2 cm = 0,42 dm et dont la hauteur est 11 cm = 1,1 dm. Il contient 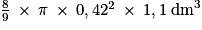 de confiture. Or on sait que 1 dm3 = 1 L.
de confiture. Or on sait que 1 dm3 = 1 L.
Par conséquent, le nombre de pots nécessaire est le quotient entier par excès de :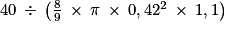 soit 74 pots.
soit 74 pots.
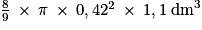 de confiture. Or on sait que 1 dm3 = 1 L.
de confiture. Or on sait que 1 dm3 = 1 L.Par conséquent, le nombre de pots nécessaire est le quotient entier par excès de :
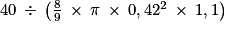 soit 74 pots.
soit 74 pots.Seules les unités de capacité sont enseignées en primaire, mais il convient de bien connaître les correspondances entre les unités de volume et de capacité, notamment 1 dm3 = 1 L pour en déduire le tableau :
Bon à savoir pour réduire sa consommation d'eau : 1 m3 = 1 000 L.
Attention : 1 cm3 = 1 mL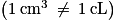 .
.
Le symbole du litre est L en majuscule… depuis 1979.
| m3 | dm3 | cm3 | ||||||
| | | kL | hL | daL | L | dL | cL | mL |
| | | 1 | 0 | 0 | 0 | | | |
| | | | | | | | 1 | 0 |
Bon à savoir pour réduire sa consommation d'eau : 1 m3 = 1 000 L.
Attention : 1 cm3 = 1 mL
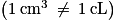 .
.Le symbole du litre est L en majuscule… depuis 1979.
Exercice 5
1. D'après l'énoncé, la frise a pour longueur 2 × 8,8 m + 7 m = 24,6 m = 2 460 cm.
Comme le maître juxtapose des feuilles de 21 cm × 29,7 cm suivant leur largeur, il lui faudra un nombre de feuilles égal au quotient entier par excès de 2 460 par 29,7, soit 83 feuilles.
Comme le maître juxtapose des feuilles de 21 cm × 29,7 cm suivant leur largeur, il lui faudra un nombre de feuilles égal au quotient entier par excès de 2 460 par 29,7, soit 83 feuilles.
2. Si on fait figurer en début de frise l'année 476 et en fin de frise l'année 2023, on fait figurer en tout 2 023 − 476 + 1 = 1 548 années.
Une année est donc représentée sur la frise par :
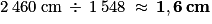 .
.
Une année est donc représentée sur la frise par :
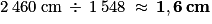 .
.3.
Le nombre de cm entre le début de la frise et cet événement est, d'après les questions précédentes, (1 492 − 476) × 2 460 ÷ 1 548 soit environ 1 614,6 cm.
Le mur nord a pour longueur 880 cm, donc cet événement n'est pas sur le mur nord.
Lorsque l'on ajoute les longueurs des murs nord et est, on trouve 880 cm + 700 cm = 1 580 cm : cet événement n'est pas non plus sur le mur est.
Par conséquent, cet événement se trouve sur le mur sud.
Vous devez savoir utiliser les fonctions habituelles d'un tableur (voir par exemple http://www.clg-monnet-briis.ac-versailles.fr/Utiliser-un-tableur ), ce qui vous permettra aussi de cerner la notion de variable, comme précisé dans le document « Utiliser le calcul littéral » sur https://eduscol.education.fr/document/17263/download
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
« L'utilisation du tableur peut faciliter la compréhension de la notion de variable dans la mesure où, dans l'édition d'une formule, ce sont les adresses des cellules (et non leur contenu) qui sont prises en compte. La modification du contenu d'une cellule désignée dans une formule modifie le contenu de la cellule où est implantée la formule, ce qui permet d'appréhender les notions de variable et de fonction. »
a.
On peut entrer dans la cellule C2 la formule =(B2−476)*(2460/1548) dans laquelle B2−476 est le nombre d'années séparant l'événement de la ligne à la fin de l'Antiquité et 2460/1548 la valeur exacte du nombre de cm pour représenter une année.
Ne pas oublier le signe = pour débuter une formule sur un tableur.
On obtient :
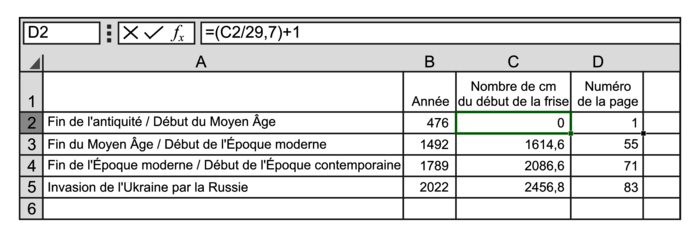 |
Remarque :
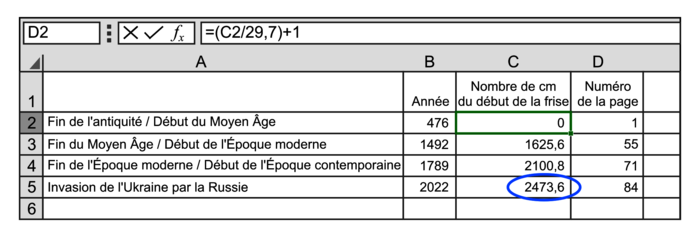
Si on avait tapé =(B2−476)*1,6, en considérant qu'une année est représentée par environ 1,6 cm, on aurait des soucis pour représenter des événements proches de l'actualité… puisqu'on devrait placer l'invasion de l'Ukraine par la Russie de 2022 à plus de 2 473 cm du début de la frise, alors qu'on ne disposerait de 2 460 cm que sur la page 84 qui n'est pas prévue !
Si on avait tapé =(B2−476)*1,6, en considérant qu'une année est représentée par environ 1,6 cm, on aurait des soucis pour représenter des événements proches de l'actualité… puisqu'on devrait placer l'invasion de l'Ukraine par la Russie de 2022 à plus de 2 473 cm du début de la frise, alors qu'on ne disposerait de 2 460 cm que sur la page 84 qui n'est pas prévue !
 |
b.
La formule permet de déterminer le numéro de la feuille sur laquelle se situe l'événement considéré, puisque la première feuille porte le n° 1 et que l'on change de feuille tous les 29,7 cm.c.
L 'accostage de Christophe Colomb sur le continent américain date de 1492.Le nombre de cm entre le début de la frise et cet événement est, d'après les questions précédentes, (1 492 − 476) × 2 460 ÷ 1 548 soit environ 1 614,6 cm.
Le mur nord a pour longueur 880 cm, donc cet événement n'est pas sur le mur nord.
Lorsque l'on ajoute les longueurs des murs nord et est, on trouve 880 cm + 700 cm = 1 580 cm : cet événement n'est pas non plus sur le mur est.
Par conséquent, cet événement se trouve sur le mur sud.
Exercice 6
1. Sur 150 élèves, 80 sont des filles, donc 150 − 80 = 70 élèves sont des garçons.
24 % des 150 élèves sont musiciens, soit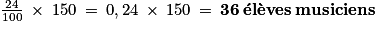 .
.
Parmi les musiciens, 16 sont des garçons, donc 36 − 16 = 20 filles sont musiciennes.
Le nombre de filles non musiciennes est donc 80 − 20 = 60.
Le nombre de garçons non musiciens est donc 70 − 16 = 54.
Le nombre total d'élèves non musiciens est 60 + 54 = 114 (ou 150 − 36 = 114).
24 % des 150 élèves sont musiciens, soit
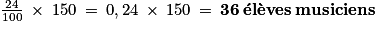 .
.Parmi les musiciens, 16 sont des garçons, donc 36 − 16 = 20 filles sont musiciennes.
Le nombre de filles non musiciennes est donc 80 − 20 = 60.
Le nombre de garçons non musiciens est donc 70 − 16 = 54.
Le nombre total d'élèves non musiciens est 60 + 54 = 114 (ou 150 − 36 = 114).
| | Nombre d'élèves musiciens | Nombre d'élèves non musiciens | Total |
| Nombre de filles | 20 | 60 | 80 |
| Nombre de garçons | 16 | 54 | 70 |
| Total | 36 | 114 | 150 |
2.
On interroge un élève au hasard : il s'agit ici d'une expérience aléatoire dont toutes les issues possibles sont équiprobables.
Si toutes les issues sont équiprobables, la probabilité d'un événement se calcule par :
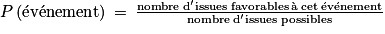 .
.
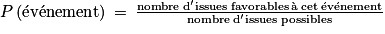 .
.a. La probabilité que ce soit un garçon est : 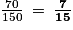 .
.
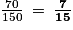 .
.b. La probabilité que ce soit une fille musicienne est : 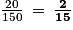 .
.
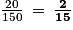 .
.c. La probabilité que ce soit un élève non musicien est : 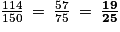 .
.
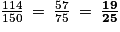 .
.3. L'élève interrogé est un garçon.
La probabilité qu'il soit musicien est :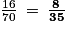 .
.
La probabilité qu'il soit musicien est :
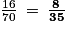 .
.4. 30 % des filles musiciennes jouent d'un instrument à vent, soit 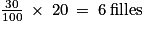 .
.
6 filles jouent d'un instrument à vent, soit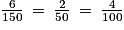 .
.
4 % du nombre total d'élèves sont des filles jouant d'un instrument à vent.
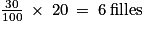 .
.6 filles jouent d'un instrument à vent, soit
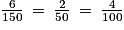 .
.4 % du nombre total d'élèves sont des filles jouant d'un instrument à vent.
Document suivant
Sujet 2023 de mathématiques, groupement académique 2
