Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
Des enseignants souhaitent créer un potager pédagogique dans la cour de leur école, en voici un plan ci-après (qui n'est pas à l'échelle).
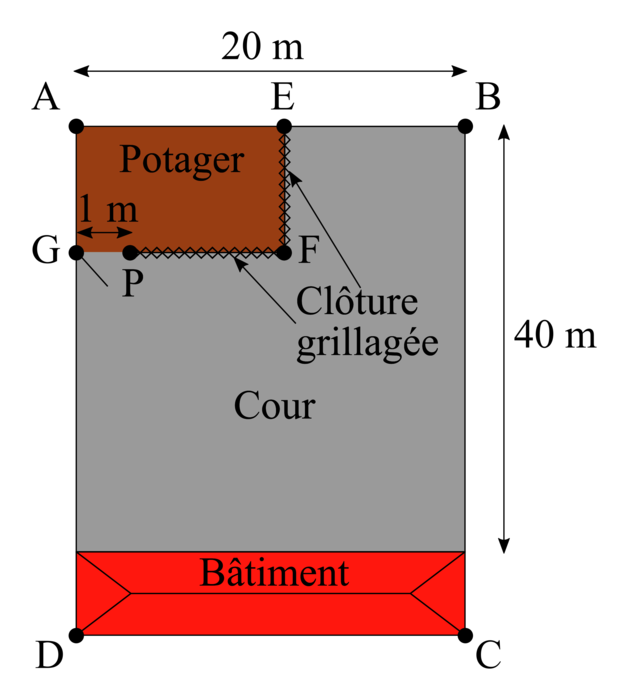 |
Le potager AEFG doit respecter les contraintes suivantes :
L'ouverture pour la porte correspond au segment [GP].
Le potager est donc le rectangle AEFG où E est un point du segment [AB] et G est un point du segment [AD] avec 5 m AG
AG  20 m.
20 m.
Pour des raisons de coût, les enseignants cherchent à déterminer les dimensions du potager afin que la longueur totale du grillage soit la plus petite possible.
- être de forme rectangulaire ;
- avoir une aire de 90 m2 ;
- être le long des murs d'enceinte [DA] et [AB] ;
- être bordé par un grillage le long des deux autres côtés ;
- disposer d'une porte de 1 m de large.
L'ouverture pour la porte correspond au segment [GP].
Le potager est donc le rectangle AEFG où E est un point du segment [AB] et G est un point du segment [AD] avec 5 m
 AG
AG  20 m.
20 m.Pour des raisons de coût, les enseignants cherchent à déterminer les dimensions du potager afin que la longueur totale du grillage soit la plus petite possible.
A. Le grillage et le potager
1.
a) Vérifier que si AG est égale à 5 m, alors la longueur de grillage est de 22 m.
b) On suppose maintenant que AG est égale à 7,5 m. Calculer la longueur du grillage nécessaire.
2.
Dans la suite, on note x la longueur de [AG], exprimée en mètres, et on appelle L la fonction qui, à tout nombre positif x compris entre 5 et 20, associe L(x) la longueur du grillage, exprimée en mètres, nécessaire pour clôturer le potager.
a) Prouver que L(x) = x + 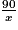 − 1.
− 1.
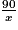 − 1.
− 1.b) Pour chacune des expressions suivantes, indiquer si elle est une autre expression de L(x). Justifier vos réponses.
i)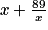 .
.
ii)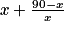 .
.
iii)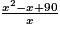 .
.
iv)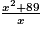 .
.
i)
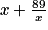 .
.ii)
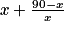 .
.iii)
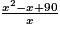 .
.iv)
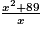 .
.3.
On donne ci-dessous une représentation graphique de la fonction L dans un repère orthogonal.
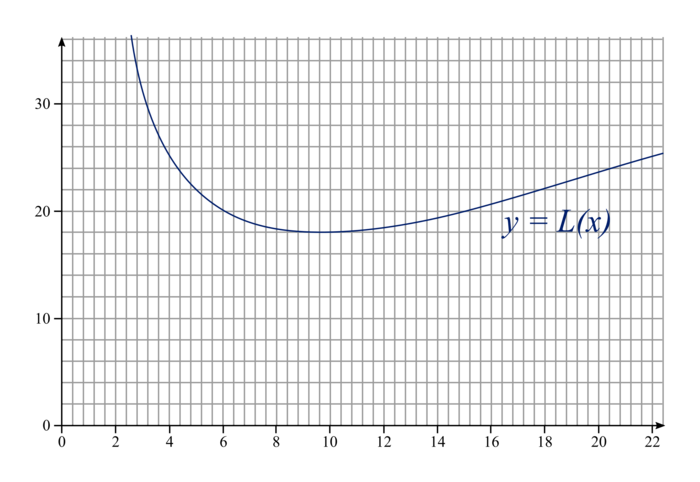 |
Déterminer graphiquement :
a) la longueur de grillage lorsque AG = 18 m ;
b) les valeurs possibles de AG lorsque la longueur de grillage est de 20 m ;
c) la valeur de AG pour que la longueur de grillage soit minimale.
B. Le compost et le potager
Le projet prévoit par ailleurs la fabrication et l'utilisation de compost pour entretenir le potager. Le bac à compost sera posé à l'extérieur du potager.
Ce bac est assimilé à un parallélépipède rectangle à base carrée de 1,6 m de côté et hauteur 1,2 m.
Ce bac est assimilé à un parallélépipède rectangle à base carrée de 1,6 m de côté et hauteur 1,2 m.
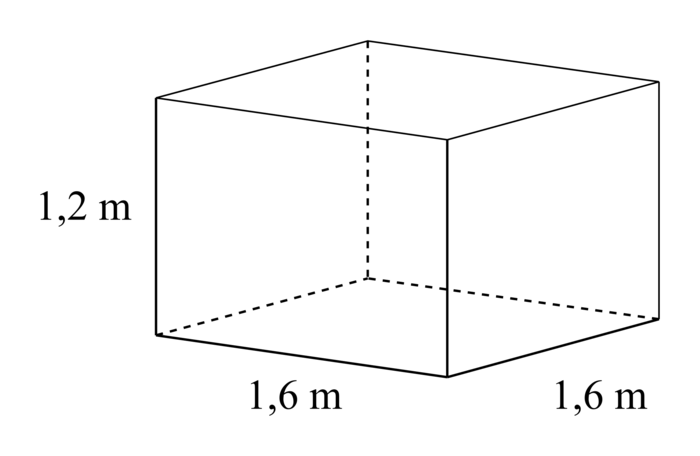 |
1. Quel est le volume du bac exprimé en m3 ?
2. Le compost se transforme naturellement et son volume diminue de 20 % par mois.
a) En remplissant le bac en totalité, quel sera le volume de compost au bout d'un mois ?
Les enseignants ont calculé l'évolution du volume de compost disponible à la fin de chaque mois d'un bac rempli. Voici ce qui a été trouvé :
Les enseignants ont calculé l'évolution du volume de compost disponible à la fin de chaque mois d'un bac rempli. Voici ce qui a été trouvé :
| A | B | C | D | E | F | G | H | I | J | K | L | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Nombre de mois | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | Volume de compost en m3 | 3,072 | 2,4576 | 1,9661 | 1,5729 | 1,2583 | 1,0066 | 0,8053 | 0,6442 | 0,5154 | 0,4123 | 0,3299 |
b) Quelle formule faut-il saisir dans la cellule C2 pour remplir ensuite l'ensemble de la ligne 2 en étirant la cellule C2 jusqu'à la cellule L2 ?
c) Plus longtemps dure la maturation du compost, meilleure sera sa qualité.
Au bout de 5 mois, la classe décide d'utiliser le compost pour les 40 m2 de plants de salades du jardin. Y a-t-il suffisamment de compost pour en épandre sur une épaisseur de 3 cm ?
Au bout de 5 mois, la classe décide d'utiliser le compost pour les 40 m2 de plants de salades du jardin. Y a-t-il suffisamment de compost pour en épandre sur une épaisseur de 3 cm ?
C. Achat des graines à planter
En période 4, les élèves décident de planter des pieds de salade. Dans le commerce, plusieurs tarifs sont proposés :
| Tarif A | Prix d'une barquette de 5 plants : 1,20 € |
|---|---|
| Tarif B | Prix d'un plant : 0,25 €, et à partir de 50 plants une réduction de 5 % est faite sur l'ensemble de la commande |
| Tarif C | Achat de carte de fidélité : 3 €, puis 0,20 € le plant |
1. Quel tarif va être le plus avantageux pour l'achat de 40 plants ?
2. L'école dispose d'un budget de 30 €. Quel tarif permet d'acheter le plus de pieds de salade ?
3. À partir de l'achat de combien de plants le tarif C devient-il plus intéressant que le tarif B ?
Deuxième partie (13 points)
Cette partie est composée de quatre exercices indépendants
Exercice 1
Le programme ci-dessous a été écrit avec le logiciel Scratch.
 |
1. Montrer que si l'utilisateur rentre le nombre 5, alors le lutin va dire 165 pendant 20 secondes.
2. Que va dire le lutin pendant 20 secondes si l'utilisateur rentre le nombre 2 + 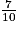 ?
?
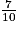 ?
?3. Quels nombres ont pu être rentrés dans « réponse » si le lutin dit « 0 » pendant 20 secondes ?
Exercice 2
Dans cet exercice, tous les dés sont équilibrés.
Arthur possède deux dés classiques (les faces sont numérotées de 1 à 6).
Juliette possède deux dés très particuliers : un patron de chacun de ces deux dés est donné ci-dessous :
Arthur possède deux dés classiques (les faces sont numérotées de 1 à 6).
Juliette possède deux dés très particuliers : un patron de chacun de ces deux dés est donné ci-dessous :
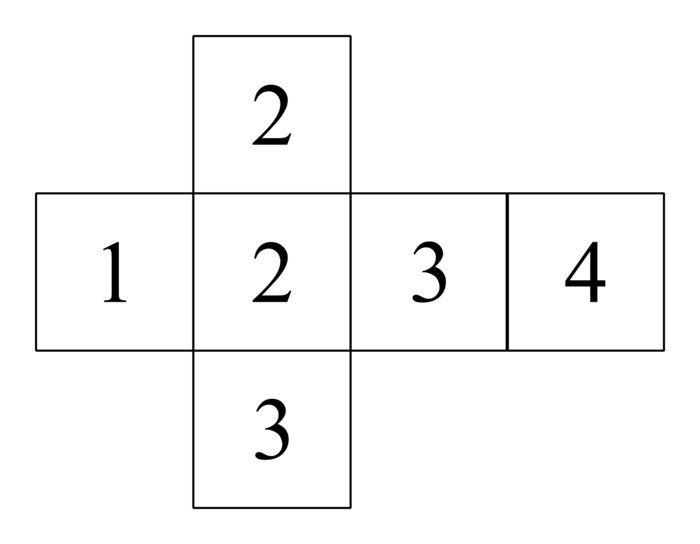 |
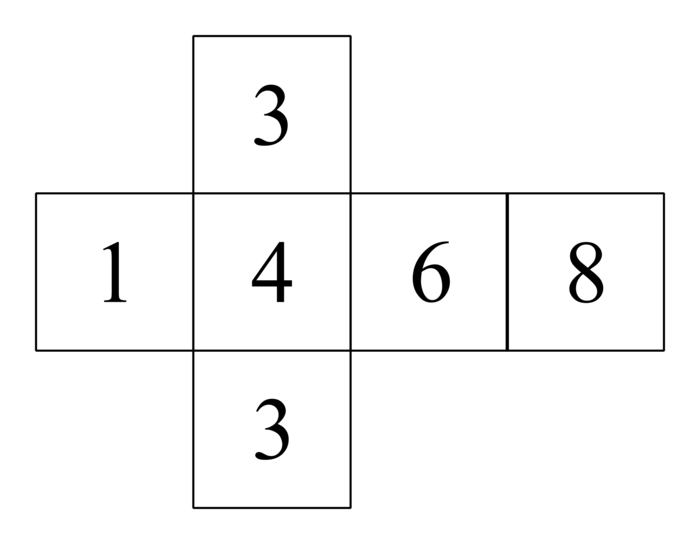 |
Arthur et Juliette définissent une règle du jeu : chacun d'eux lance ses deux dés puis additionne les deux nombres qu'il a obtenus.
1. Lors de leur premier lancer, Juliette et Arthur ont tous deux obtenu une somme égale à 5. Qui, de Juliette ou d'Arthur, avait le plus de chances d'obtenir 5 ?
2. Arthur prétend que, s'il lance ses dés classiques, la somme ayant la plus grande probabilité d'être obtenue est 7. Est-ce exact ? Justifier la réponse.
3. Juliette dispose d'un tableau de synthèse résultant d'une simulation de 1 000 lancers de ses deux dés.
| Somme | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Effectif | 32 | 51 | 122 | 174 | 151 | 151 | 79 | 81 | 89 | 48 | 22 |
a) En observant ce tableau, elle affirme que lorsqu'elle lance ses dés, la probabilité d'obtenir 6 est égale à celle d'obtenir un 7. Le tableau permet-il effectivement de l'affirmer ?
b) Calculer la probabilité d'obtenir un 6 et celle d'obtenir un 7 avec les dés de Juliette.
Exercice 3
Sarah choisit un nombre entier. À la somme des carrés des deux entiers qui lui succèdent, elle retranche la somme des carrés des deux entiers qui le précèdent.
1. Montrer qu'en appliquant ce calcul à 7 on trouve 84.
2. Calculer le résultat obtenu si l'on choisit le nombre 5.
3. On reporte dans un tableau les résultats obtenus pour plusieurs calculs :
Conjecturer une méthode permettant de retrouver le nombre choisi connaissant le résultat.
| Nombre choisi | −37 | 0 | 2 | 7 | 10 | 30 |
|---|---|---|---|---|---|---|
| Résultat obtenu | −444 | 0 | 24 | 84 | 120 | 360 |
Conjecturer une méthode permettant de retrouver le nombre choisi connaissant le résultat.
4. Démontrer la conjecture.
Exercice 4
Le pavage ci-dessous est composé de 18 pentagones tous superposables. Quatre d'entre eux ont été numérotés.
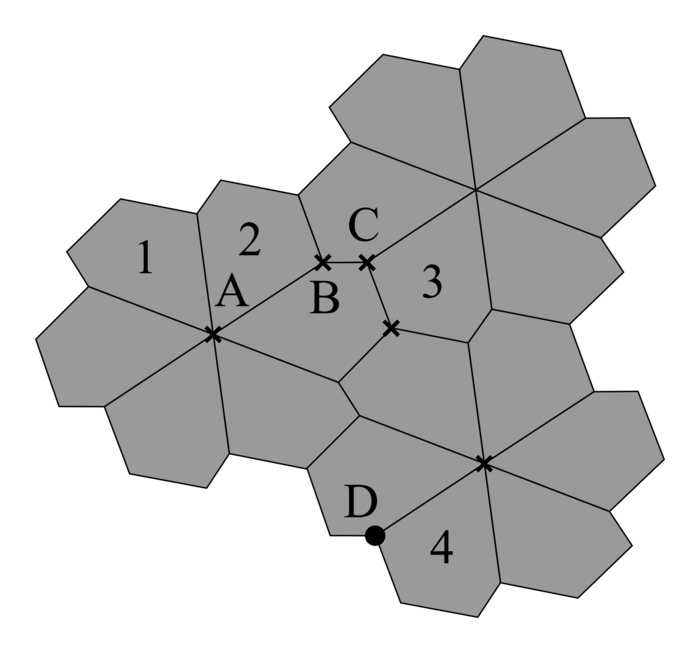 |
Indiquer quelle transformation (translation, rotation, symétrie) permet de passer :
a) du pentagone 1 au pentagone 2 ;
b) du pentagone 2 au pentagone 3 ;
c) du pentagone 3 au pentagone 4.
Préciser dans chaque cas les éléments qui définissent la transformation choisie. Aucune justification n'est attendue.
a) du pentagone 1 au pentagone 2 ;
b) du pentagone 2 au pentagone 3 ;
c) du pentagone 3 au pentagone 4.
Préciser dans chaque cas les éléments qui définissent la transformation choisie. Aucune justification n'est attendue.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Une enseignante veut faire renforcer la capacité « Utiliser le nombre pour repérer une position » chez ses élèves de grande section. Elle leur propose l'activité ci-dessous.
Un train modèle de 31 wagons est décoré avec des images toutes différentes et facilement reconnaissables.
L'élève dispose :
Phase 1
L'enseignant propose de faire l'activité en positionnant le train personnel juste en dessous du train modèle. Quand l'élève a reproduit le train modèle, la correspondance terme à terme est introduite par le maître comme procédure de vérification.
L'élève dispose :
- d'un train personnel de même longueur, non décoré ;
- d'images identiques à celles du train modèle.
Phase 1
L'enseignant propose de faire l'activité en positionnant le train personnel juste en dessous du train modèle. Quand l'élève a reproduit le train modèle, la correspondance terme à terme est introduite par le maître comme procédure de vérification.
 |
Phase 2
La consigne est identique, mais le train modèle est placé à distance de l'élève, hors de son champ visuel. L'élève n'a pas le droit de déplacer son train pour le décorer. Cependant, l'élève pourra se déplacer autant de fois que nécessaire pour reproduire le modèle.
La consigne est identique, mais le train modèle est placé à distance de l'élève, hors de son champ visuel. L'élève n'a pas le droit de déplacer son train pour le décorer. Cependant, l'élève pourra se déplacer autant de fois que nécessaire pour reproduire le modèle.
1. Quelles vérifications permettent la phase 1 avant de proposer la phase 2 aux élèves ? Formuler deux attendus pour la première phase.
Pour la phase 2, l'enseignante a imaginé les deux situations suivantes :
Pour la phase 2, l'enseignante a imaginé les deux situations suivantes :
- Train modèle 1
 |
- Train modèle 2
 |
2. Les deux trains ci-dessus permettent-ils de mobiliser de la même manière la capacité visée ?
3. Citer les étapes que doit réaliser un élève pour réussir la tâche demandée dans la phase 2.
4.
a) Sacha sait compter jusqu'à 8. Décrire comment Sacha peut procéder pour placer avec succès chacune des trois images du train modèle 2.
b) Comment Sacha peut-il savoir s'il a réussi ?
Situation 2
Le problème suivant a été proposé en fin d'année à des élèves d'une classe de CE1.
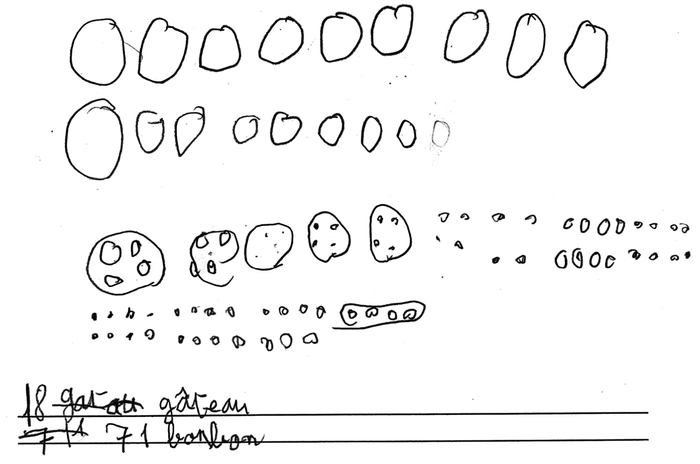
18 enfants sont réunis pour goûter. Chaque enfant reçoit 1 gâteau et 4 bonbons.
|
1. Analyse des productions
a) Quels points communs et quelles différences peut-on mettre en évidence dans les procédures de Maëlys et de Malyan ?
 |
 |
b) Quels points communs et quelles différences peut-on mettre en évidence dans les procédures de Bérénice et de Mila ?
 |
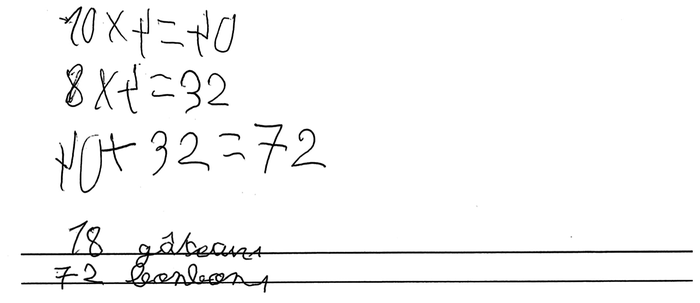 |
2. La réponse ci-dessous est celle donnée par Martin. L'enseignant propose alors à Martin un nouveau problème où le nombre d'enfants passe de 18 à 32. En quoi cette modification peut-elle influencer la production de Martin ?
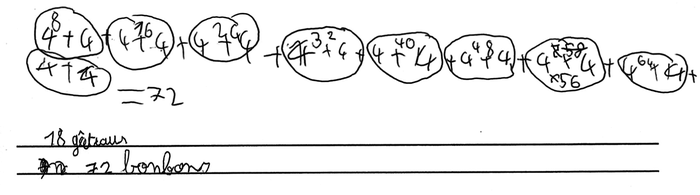 |
3. En quoi la représentation de Maëlys peut-elle être une illustration des calculs effectués par Martin et Bérénice ? Quelle propriété de la multiplication cette comparaison induit-elle ?
Situation 3
1. Voici deux réponses d'élèves à la question « Dans un nombre, à quoi sert la virgule ? » posée par un enseignant dans une classe de CM1 :
- Élève A : « La virgule sert à montrer que c'est un nombre décimal. »
- Élève B : « La virgule sert à séparer le nombre entier et la partie décimale. »
a) Pour chacune des réponses proposées, expliquer pourquoi elle ne peut pas être retenue par l'enseignant pour la trace écrite à noter dans les cahiers d'élèves.
b) Quelle réponse à la question posée l'enseignant peut-il proposer à la classe ?
2. Voici une production d'élève :
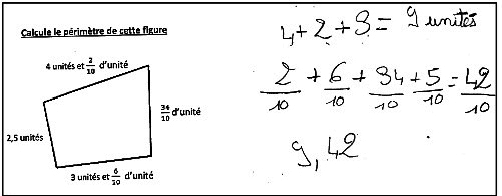 |
a) Analyser la production de l'élève en relevant ses réussites et ses erreurs.
b) Que peut-on proposer à l'élève pour l'aider à corriger ses éventuelles erreurs ?
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Le grillage et le potager
1. Calcul de la longueur du grillage pour deux valeurs particulières de AG
a) Longueur du grillage pour AG = 5 m
L'aire du rectangle AEFG étant imposée à 90 m2, si la longueur AG est 5 m, alors la longueur AE est :
AE = 90 m2 ÷ 5 m = 18 m.
La longueur du grillage est :
l = PF + FE = AE − 1 m + AG = 18 m − 1 m + 5 m = 22 m.
Ainsi, pour une longueur AG de 5 m, le grillage a une longueur de 22 m.
L'aire du rectangle AEFG étant imposée à 90 m2, si la longueur AG est 5 m, alors la longueur AE est :
AE = 90 m2 ÷ 5 m = 18 m.
La longueur du grillage est :
l = PF + FE = AE − 1 m + AG = 18 m − 1 m + 5 m = 22 m.
Ainsi, pour une longueur AG de 5 m, le grillage a une longueur de 22 m.
b) Longueur du grillage pour AG = 7,5 m
L'aire du rectangle AEFG étant imposée à 90 m2, si la longueur AG est 7,5 m, alors la longueur AE est :
AE = 90 m2 ÷ 7,5 m = 12 m.
La longueur du grillage est :
l = PF + FE = AE − 1 m + AG = 12 m − 1 m + 7,5 m = 18,5 m.
Ainsi, pour une longueur AG de 7,5 m, le grillage a une longueur de 18,5 m.
L'aire du rectangle AEFG étant imposée à 90 m2, si la longueur AG est 7,5 m, alors la longueur AE est :
AE = 90 m2 ÷ 7,5 m = 12 m.
La longueur du grillage est :
l = PF + FE = AE − 1 m + AG = 12 m − 1 m + 7,5 m = 18,5 m.
Ainsi, pour une longueur AG de 7,5 m, le grillage a une longueur de 18,5 m.
2. Expression de la longueur du grillage en fonction de AG
a) Détermination de l'expression L(x)
Soit x la mesure en mètres de la longueur AG.
Alors, puisque l'aire de AEFG est 90 m2, la mesure en mètres de la longueur AE est :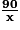 .
.
Si l est la longueur du grillage, alors : l = PF + FE = AE − 1 m + AG.
Si L(x) est la mesure en mètres de la longueur du grillage, alors :
L(x) =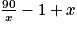 =
= 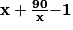 .
.
Soit x la mesure en mètres de la longueur AG.
Alors, puisque l'aire de AEFG est 90 m2, la mesure en mètres de la longueur AE est :
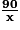 .
.Si l est la longueur du grillage, alors : l = PF + FE = AE − 1 m + AG.
Si L(x) est la mesure en mètres de la longueur du grillage, alors :
L(x) =
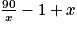 =
= 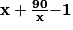 .
.b) Autres expressions de L(x)
i)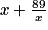
Pour x = 2, cette expression vaut : 2 +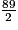 = 2 + 44,5 = 46,5.
= 2 + 44,5 = 46,5.
Or, L(2) = 2 +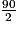 − 1 = 2 + 45 − 1 = 46 (et 46
− 1 = 2 + 45 − 1 = 46 (et 46 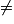 46,5).
46,5).
Ce n'est donc pas une autre expression de L(x).
ii)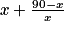
L(x) =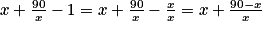 .
.
C'est donc bien une autre expression de L(x).
iii)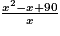
L(x) = .
.
C'est donc bien une autre expression de L(x).
iv)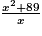
Pour x = 2, cette expression vaut :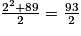 = 46,5.
= 46,5.
Et nous avons déjà vu que L(2) = 46.
Ce n'est donc pas une autre expression de L(x).
i)
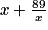
Pour x = 2, cette expression vaut : 2 +
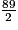 = 2 + 44,5 = 46,5.
= 2 + 44,5 = 46,5.Or, L(2) = 2 +
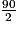 − 1 = 2 + 45 − 1 = 46 (et 46
− 1 = 2 + 45 − 1 = 46 (et 46 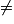 46,5).
46,5).Ce n'est donc pas une autre expression de L(x).
ii)
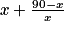
L(x) =
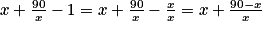 .
.C'est donc bien une autre expression de L(x).
iii)
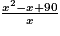
L(x) =
 .
.C'est donc bien une autre expression de L(x).
iv)
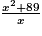
Pour x = 2, cette expression vaut :
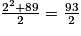 = 46,5.
= 46,5.Et nous avons déjà vu que L(2) = 46.
Ce n'est donc pas une autre expression de L(x).
En définitive, les autres expressions de L(x) sont ii) et iii).
3. Représentation graphique de L entre 5 et 20
a) Valeur de la longueur du grillage pour AG = 18 m
L'axe des ordonnées subdivise la graduation principale, de largeur 10, en cinq intervalles.
Ainsi, la graduation secondaire vaut 10 ÷ 5 = 2.
On lit sur le graphique que l'image de 18 correspond environ à la graduation immédiatement après 20, soit donc 22 mètres.
L'axe des ordonnées subdivise la graduation principale, de largeur 10, en cinq intervalles.
Ainsi, la graduation secondaire vaut 10 ÷ 5 = 2.
On lit sur le graphique que l'image de 18 correspond environ à la graduation immédiatement après 20, soit donc 22 mètres.
b) Valeurs de AG pour une longueur de grillage de 20 m
L'axe des abscisses subdivise la graduation principale, de largeur 2, en cinq intervalles.
Ainsi, la graduation secondaire vaut 2 ÷ 5 = 0,4.
On lit sur le graphique que les antécédents de 20 sont :
L'axe des abscisses subdivise la graduation principale, de largeur 2, en cinq intervalles.
Ainsi, la graduation secondaire vaut 2 ÷ 5 = 0,4.
On lit sur le graphique que les antécédents de 20 sont :
- environ 6 (lecture directe) ;
- environ 15 (milieu des deuxième et troisième graduations après 14 : 14,8 et 15,2).
c) Valeurs de AG pour une longueur de grillage minimale
Il n'est pas facile de donner une valeur précise de AG, car la courbe est plutôt plate dans la zone minimale. On peut dire que, pour une longueur minimale de grillage, AG se situe entre 8,4 et 10,8 mètres.
Il n'est pas facile de donner une valeur précise de AG, car la courbe est plutôt plate dans la zone minimale. On peut dire que, pour une longueur minimale de grillage, AG se situe entre 8,4 et 10,8 mètres.
B. Le compost et le potager
1. Volume du bac à compost
Le bac étant assimilé à un pavé droit, son volume est :
Vbac = 1,2 m × (1,6 m)2 = 3,072 m3.
Le volume du bac à compost est d'environ 3 mètres cubes.
Le bac étant assimilé à un pavé droit, son volume est :
Vbac = 1,2 m × (1,6 m)2 = 3,072 m3.
Le volume du bac à compost est d'environ 3 mètres cubes.
2. Évolution du volume de compost
a) Volume après une diminution de 20 %
3,072 × (1 − 0,2) = 3,072 × 0,8 = 2,4576.
Au bout d'un mois, le volume du compost sera d'environ 2,5 mètres cubes.
3,072 × (1 − 0,2) = 3,072 × 0,8 = 2,4576.
Au bout d'un mois, le volume du compost sera d'environ 2,5 mètres cubes.
b) Formule de l'évolution du volume dans un tableur
Il existe deux possibilités pour la formule de la cellule C2 :
Il existe deux possibilités pour la formule de la cellule C2 :
- Soit on calcule une diminution de 20 % à partir de la valeur du mois précédent, ce qui donne la formule suivante : =B2*0,8. Cette formule se transformera en =C2*0,8 dans la cellule D2, ce qui est bien ce que l'on veut.
- Soit on calcule directement la diminution totale, à partir du volume de départ, qui dépend du nombre de mois, nombre indiqué sur la ligne du dessus, auquel cas la formule est la suivante : =$B2*(0,8)^C1. Dans ce cas, il faut bloquer la référence « colonne » de la cellule B2 grâce au symbole $.
c) Quantité de compost pour les plants de salade
40 m2 de compost sur une épaisseur de 3 cm demandent un volume de compost de :
40 m2 × 3 cm = 40 m2 × 0,03 m = 1,2 m3.
On lit dans le tableau que le volume disponible au bout de 5 mois est 1,0066 m3.
Il n'y aura donc pas assez de compost pour l'épandre sur une épaisseur de 3 cm.
40 m2 de compost sur une épaisseur de 3 cm demandent un volume de compost de :
40 m2 × 3 cm = 40 m2 × 0,03 m = 1,2 m3.
On lit dans le tableau que le volume disponible au bout de 5 mois est 1,0066 m3.
Il n'y aura donc pas assez de compost pour l'épandre sur une épaisseur de 3 cm.
C. Achat des graines à planter
1. Tarif le plus avantageux pour l'achat de 40 plants
Tarif A
40 plants par barquette de 5 plants, cela fait 40 ÷ 5 = 8 barquettes.
À 1,20 € la barquette, l'achat de 40 plants revient à 8 × 1,20 € = 9,60 €.
Tarif B
À 0,25 € le plant, l'achat de 40 plants revient à 40 × 0,25 € = 10 €.
Tarif C
À 0,20 € le plant, 40 plants valent 40 × 0,20 € = 8 €.
Avec les 3 euros que coûte la carte de fidélité, l'achat de 40 plants revient à 11 €.
C'est le tarif A le plus avantageux pour l'achat de 40 plants.
Tarif A
40 plants par barquette de 5 plants, cela fait 40 ÷ 5 = 8 barquettes.
À 1,20 € la barquette, l'achat de 40 plants revient à 8 × 1,20 € = 9,60 €.
Tarif B
À 0,25 € le plant, l'achat de 40 plants revient à 40 × 0,25 € = 10 €.
Tarif C
À 0,20 € le plant, 40 plants valent 40 × 0,20 € = 8 €.
Avec les 3 euros que coûte la carte de fidélité, l'achat de 40 plants revient à 11 €.
C'est le tarif A le plus avantageux pour l'achat de 40 plants.
2. Tarif le plus avantageux pour une dépense de 30 euros
Tarif A
30 € ÷ 1,20 € = 25.
On peut acheter 25 barquettes de 5 plants chacune, soit 125 plants.
Tarif B
30 € ÷ 0,25 € = 120.
On dépasse largement la quantité de 50 plants.
Une réduction de 5 % a donc été effectuée :
30 € ÷ (1 − 0,05) = 30 € ÷ 0,95 31,58 € : somme disponible pour acheter les plants.
31,58 € : somme disponible pour acheter les plants.
31,58 € ÷ 0,25 126,3 : valeur approchée du nombre de plants que l'on peut acheter.
126,3 : valeur approchée du nombre de plants que l'on peut acheter.
On peut donc acheter 126 plants avec 30 €.
Tarif C
30 € − 3 € = 27 € et 27 € ÷ 0,20 = 135.
On peut acheter 135 plants pour 30 € avec le tarif C.
C'est donc le tarif C le plus avantageux pour acheter des plants avec 30 €.
Tarif A
30 € ÷ 1,20 € = 25.
On peut acheter 25 barquettes de 5 plants chacune, soit 125 plants.
Tarif B
30 € ÷ 0,25 € = 120.
On dépasse largement la quantité de 50 plants.
Une réduction de 5 % a donc été effectuée :
30 € ÷ (1 − 0,05) = 30 € ÷ 0,95
 31,58 € : somme disponible pour acheter les plants.
31,58 € : somme disponible pour acheter les plants.31,58 € ÷ 0,25
 126,3 : valeur approchée du nombre de plants que l'on peut acheter.
126,3 : valeur approchée du nombre de plants que l'on peut acheter.On peut donc acheter 126 plants avec 30 €.
Tarif C
30 € − 3 € = 27 € et 27 € ÷ 0,20 = 135.
On peut acheter 135 plants pour 30 € avec le tarif C.
C'est donc le tarif C le plus avantageux pour acheter des plants avec 30 €.
3. Tarif le plus avantageux entre les tarifs B et C
Nous avons vu que, pour 40 plants, le tarif B est plus avantageux que le C, et que, pour 30 €, le tarif C est plus avantageux que le B.
Si nous appelons n le nombre de plants, TB(n) et TC(n) les coûts pour n plants respectivement pour les tarifs B et C, alors :
TB(n) = 0,25n pour n < 50, et TB(n) = 0,25n × 0,95 = 0,2375n pour n 50.
50.
TC(n) = 0,2n + 3.
On cherche la ou les valeurs de n pour lesquelles TC(n) TB(n).
TB(n).
A priori, nous ignorons laquelle des deux expressions de TB il faut choisir.
Commençons par la première et résolvons l'inéquation :
0,2n + 3 0,25n
0,25n
0,25n − 0,2n 3
3
0,05n 3
3
n 3 ÷ 0,05
3 ÷ 0,05
n 60, ce qui ne se vérifie jamais puisque cette inéquation n'est valable que pour n
60, ce qui ne se vérifie jamais puisque cette inéquation n'est valable que pour n  50.
50.
On peut d'ores et déjà affirmer que le tarif B est toujours plus avantageux que le tarif C pour moins de 50 plants.
Résolvons la seconde inéquation, valable pour plus de 50 plants :
0,2n + 3 0,2375n
0,2375n
0,2375n − 0,2n 3
3
0,0375n 3
3
n 3 ÷ 0,0375
3 ÷ 0,0375
n 80
80
Ainsi, le tarif C devient plus avantageux que le tarif B à partir de 80 plants.
Nous avons vu que, pour 40 plants, le tarif B est plus avantageux que le C, et que, pour 30 €, le tarif C est plus avantageux que le B.
Si nous appelons n le nombre de plants, TB(n) et TC(n) les coûts pour n plants respectivement pour les tarifs B et C, alors :
TB(n) = 0,25n pour n < 50, et TB(n) = 0,25n × 0,95 = 0,2375n pour n
 50.
50.TC(n) = 0,2n + 3.
On cherche la ou les valeurs de n pour lesquelles TC(n)
 TB(n).
TB(n).A priori, nous ignorons laquelle des deux expressions de TB il faut choisir.
Commençons par la première et résolvons l'inéquation :
0,2n + 3
 0,25n
0,25n0,25n − 0,2n
 3
30,05n
 3
3n
 3 ÷ 0,05
3 ÷ 0,05n
 60, ce qui ne se vérifie jamais puisque cette inéquation n'est valable que pour n
60, ce qui ne se vérifie jamais puisque cette inéquation n'est valable que pour n  50.
50.On peut d'ores et déjà affirmer que le tarif B est toujours plus avantageux que le tarif C pour moins de 50 plants.
Résolvons la seconde inéquation, valable pour plus de 50 plants :
0,2n + 3
 0,2375n
0,2375n0,2375n − 0,2n
 3
30,0375n
 3
3n
 3 ÷ 0,0375
3 ÷ 0,0375n
 80
80Ainsi, le tarif C devient plus avantageux que le tarif B à partir de 80 plants.
Deuxième partie
Exercice 1
1. Calcul de l'image de 5
Le nombre choisi est 5.
On ajoute 6 au nombre choisi : 5 + 6 = 11 et on appelle x cette valeur.
On multiplie par 3 le nombre choisi : 3 × 5 = 15 et on appelle y cette valeur.
On effectue le produit xy : 11 × 15 = 165.
L'image de 5 par le programme est bien 165.
Le nombre choisi est 5.
On ajoute 6 au nombre choisi : 5 + 6 = 11 et on appelle x cette valeur.
On multiplie par 3 le nombre choisi : 3 × 5 = 15 et on appelle y cette valeur.
On effectue le produit xy : 11 × 15 = 165.
L'image de 5 par le programme est bien 165.
2. Calcul de l'image de 2 + 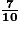
Le nombre choisi est 2,7.
On ajoute 6 au nombre choisi : 2,7 + 6 = 8,7 et on appelle x cette valeur.
On multiplie par 3 le nombre choisi : 3 × 2,7 = 8,1 et on appelle y cette valeur.
On effectue le produit xy : 8,7 × 8,1 = 70,47.
Si on rentre le nombre 2 +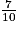 , le lutin va dire 70,47 pendant 20 secondes.
, le lutin va dire 70,47 pendant 20 secondes.
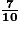
Le nombre choisi est 2,7.
On ajoute 6 au nombre choisi : 2,7 + 6 = 8,7 et on appelle x cette valeur.
On multiplie par 3 le nombre choisi : 3 × 2,7 = 8,1 et on appelle y cette valeur.
On effectue le produit xy : 8,7 × 8,1 = 70,47.
Si on rentre le nombre 2 +
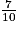 , le lutin va dire 70,47 pendant 20 secondes.
, le lutin va dire 70,47 pendant 20 secondes.3. Nombre choisi au départ pour que le lutin dise « 0 » pendant 20 secondes
Si l'on regarde la dernière instruction du programme, on constate qu'il faut que le produit xy soit nul.
Or, pour qu'un produit soit nul, il faut et il suffit que l'un de ses facteurs soit nul, soit ici x = 0 ou y = 0.
Si l'on appelle n le nombre choisi, x = n + 6 et y = 3n.
Pour obtenir 0, il faut donc que :
Si l'on regarde la dernière instruction du programme, on constate qu'il faut que le produit xy soit nul.
Or, pour qu'un produit soit nul, il faut et il suffit que l'un de ses facteurs soit nul, soit ici x = 0 ou y = 0.
Si l'on appelle n le nombre choisi, x = n + 6 et y = 3n.
Pour obtenir 0, il faut donc que :
- soit n + 6 = 0, ce qui revient à n = −6.
- soit 3n = 0, ce qui revient à n = 0.
Exercice 2
1. Probabilité d'obtenir un total de 5 avec chacun des dés
Présentons les sommes pouvant être obtenues à l'aide d'un tableau à double entrée.
Dés de Juliette
Dés d'Arthur
Il y a 36 issues (sommes) possibles dans les deux cas.
Juliette avait 6 possibilités d'obtenir une somme égale à 5. Pour elle, la probabilité d'obtenir 5 est donc de 6/36 = 1/6.
Pour Arthur, la probabilité d'obtenir une somme égale à 5 est de 4/36 = 1/9.
Juliette avait plus de chances d'obtenir 5 qu'Arthur.
Présentons les sommes pouvant être obtenues à l'aide d'un tableau à double entrée.
Dés de Juliette
| Dé n° 1 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 2 | 3 | 3 | 4 | ||
| Dé n° 2 | 1 | 2 | 3 | 3 | 4 | 4 | 5 |
| 3 | 4 | 5 | 5 | 6 | 6 | 7 | |
| 3 | 4 | 5 | 5 | 6 | 6 | 7 | |
| 4 | 5 | 6 | 6 | 7 | 7 | 8 | |
| 6 | 7 | 8 | 8 | 9 | 9 | 10 | |
| 8 | 9 | 10 | 10 | 11 | 11 | 12 | |
Dés d'Arthur
| Dé n° 1 | |||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | ||
| Dé n° 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
Il y a 36 issues (sommes) possibles dans les deux cas.
Juliette avait 6 possibilités d'obtenir une somme égale à 5. Pour elle, la probabilité d'obtenir 5 est donc de 6/36 = 1/6.
Pour Arthur, la probabilité d'obtenir une somme égale à 5 est de 4/36 = 1/9.
Juliette avait plus de chances d'obtenir 5 qu'Arthur.
2. Somme ayant la plus grande probabilité d'être obtenue par Arthur
Le tableau ci-dessus permet de dénombrer les occurrences théoriques des différentes sommes pour Arthur et de constater que, avec 6 occurrences, 7 est la somme ayant la plus grande probabilité d'être obtenue, avec une probabilité de 6/36, soit 1/6.
Arthur a raison.
Le tableau ci-dessus permet de dénombrer les occurrences théoriques des différentes sommes pour Arthur et de constater que, avec 6 occurrences, 7 est la somme ayant la plus grande probabilité d'être obtenue, avec une probabilité de 6/36, soit 1/6.
Arthur a raison.
3.
1. Lors d'une expérience qui a eu lieu (passée, réelle), on peut calculer la fréquence d'apparition d'un événement particulier, par exemple la fréquence d'apparition du chiffre 3 lors de plusieurs lancers successifs d'un dé.
Cette fréquence dépend du nombre d'expériences qui a eu lieu. Si, au bout de 10 lancers, 3 est apparu 4 fois, alors sa fréquence d'apparition est 4/10 = 0,4.
2. À propos d'une expérience aléatoire que l'on peut décrire et modéliser et dont on veut prévoir les différentes issues (futures, virtuelles donc), on peut calculer la probabilité d'apparition d'un événement particulier, par exemple la probabilité d'obtenir le chiffre 3 lors du lancer d'un dé.
Cette probabilité ne dépend que des caractéristiques de l'expérience. Ici, un dé ayant 6 faces et toutes les faces ayant la même chance d'apparaître, la probabilité d'obtenir 3 est 1/6.
3. Il existe un phénomène, appelé « stabilisation des fréquences », que l'on peut constater expérimentalement en faisant un grand nombre d'expériences successives, et que l'on peut démontrer grâce à un théorème intitulé « Loi des grands nombres ».
Cette loi est la suivante : plus le nombre d'expérience est grand, et plus la fréquence d'apparition d'un événement se stabilise (i. e. varie de moins en moins) autour d'une valeur égale à la probabilité théorique d'apparition de cet événement.
Autrement dit, plus on lancera le dé, et plus la fréquence d'apparition du chiffre 3 se stabilisera autour de la valeur 1/6.
 0,166667 diffère de moins de 2 centièmes de la fréquence d'apparition du 6 après 1 000 lancers.
0,166667 diffère de moins de 2 centièmes de la fréquence d'apparition du 6 après 1 000 lancers.
De même, P(7) 0,139 diffère d'à peine plus de 1 centième de la fréquence d'apparition du 7 après 1 000 lancers.
0,139 diffère d'à peine plus de 1 centième de la fréquence d'apparition du 7 après 1 000 lancers.
a) Interprétation du tableau
Remarque
Cette question fait le lien entre fréquence et probabilités.1. Lors d'une expérience qui a eu lieu (passée, réelle), on peut calculer la fréquence d'apparition d'un événement particulier, par exemple la fréquence d'apparition du chiffre 3 lors de plusieurs lancers successifs d'un dé.
Cette fréquence dépend du nombre d'expériences qui a eu lieu. Si, au bout de 10 lancers, 3 est apparu 4 fois, alors sa fréquence d'apparition est 4/10 = 0,4.
2. À propos d'une expérience aléatoire que l'on peut décrire et modéliser et dont on veut prévoir les différentes issues (futures, virtuelles donc), on peut calculer la probabilité d'apparition d'un événement particulier, par exemple la probabilité d'obtenir le chiffre 3 lors du lancer d'un dé.
Cette probabilité ne dépend que des caractéristiques de l'expérience. Ici, un dé ayant 6 faces et toutes les faces ayant la même chance d'apparaître, la probabilité d'obtenir 3 est 1/6.
3. Il existe un phénomène, appelé « stabilisation des fréquences », que l'on peut constater expérimentalement en faisant un grand nombre d'expériences successives, et que l'on peut démontrer grâce à un théorème intitulé « Loi des grands nombres ».
Cette loi est la suivante : plus le nombre d'expérience est grand, et plus la fréquence d'apparition d'un événement se stabilise (i. e. varie de moins en moins) autour d'une valeur égale à la probabilité théorique d'apparition de cet événement.
Autrement dit, plus on lancera le dé, et plus la fréquence d'apparition du chiffre 3 se stabilisera autour de la valeur 1/6.
Le tableau permet d'affirmer que les occurrences de 6 et 7, sur cette simulation, sont les mêmes.
Donc, les fréquences d'apparition de 6 et 7 sont les mêmes après 1 000 lancers, toutes deux égales à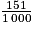 = 0,151.
= 0,151.
On ne peut toutefois pas en déduire que la probabilité théorique d'obtenir 6 est égale à celle d'obtenir 7.
La fréquence d'apparition d'une issue se stabilise vers la probabilité théorique lorsque l'on fait tendre le nombre de simulations vers l'infini ; 1 000 n'est pas un nombre suffisant de simulations.
Donc, les fréquences d'apparition de 6 et 7 sont les mêmes après 1 000 lancers, toutes deux égales à
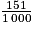 = 0,151.
= 0,151.On ne peut toutefois pas en déduire que la probabilité théorique d'obtenir 6 est égale à celle d'obtenir 7.
La fréquence d'apparition d'une issue se stabilise vers la probabilité théorique lorsque l'on fait tendre le nombre de simulations vers l'infini ; 1 000 n'est pas un nombre suffisant de simulations.
b) Calcul de la probabilité d'obtenir 6 (resp. 7) pour Juliette
Référons-nous au tableau ci-dessus, concernant les dés de Juliette :
P(6) = 6/36 = 1/6.
P(7) = 5/36.
Référons-nous au tableau ci-dessus, concernant les dés de Juliette :
P(6) = 6/36 = 1/6.
P(7) = 5/36.
Remarque
Notons que P(6)  0,166667 diffère de moins de 2 centièmes de la fréquence d'apparition du 6 après 1 000 lancers.
0,166667 diffère de moins de 2 centièmes de la fréquence d'apparition du 6 après 1 000 lancers.De même, P(7)
 0,139 diffère d'à peine plus de 1 centième de la fréquence d'apparition du 7 après 1 000 lancers.
0,139 diffère d'à peine plus de 1 centième de la fréquence d'apparition du 7 après 1 000 lancers.Exercice 3
1. Appliquons le programme de calcul à 7
82 + 92 − (62 + 52) = 64 + 81 − (36 + 25) = 145 − 61 = 84.
82 + 92 − (62 + 52) = 64 + 81 − (36 + 25) = 145 − 61 = 84.
2. Résultat obtenu si on choisit 5
62 + 72 − (42 + 32) = 36 + 49 − (16 + 9) = 85 − 25 = 60.
62 + 72 − (42 + 32) = 36 + 49 − (16 + 9) = 85 − 25 = 60.
3. Conjecture
−444 = 12 × (−37) ; 0 = 12 × 0 ; 24 = 12 × 2 ; 84 = 12 × 7 ; 120 = 12 × 10 ; 360 = 12 × 30.
Il semblerait que le résultat obtenu soit égal à 12 fois le nombre choisi ; ainsi, pour trouver le nombre choisi à partir du résultat, il suffirait de diviser celui-ci par 12.
−444 = 12 × (−37) ; 0 = 12 × 0 ; 24 = 12 × 2 ; 84 = 12 × 7 ; 120 = 12 × 10 ; 360 = 12 × 30.
Il semblerait que le résultat obtenu soit égal à 12 fois le nombre choisi ; ainsi, pour trouver le nombre choisi à partir du résultat, il suffirait de diviser celui-ci par 12.
4. Démonstration
Soit x le nombre choisi. Le programme s'écrit :
(x + 1)2 + (x + 2)2 − [(x − 1)2 − (x − 2)2] = x2 + 2x + 1 + x2 + 4x + 4 − (x2 − 2x + 1 + x2 − 4x + 4)
= 2x2 + 6x + 5 − (2x2 − 6x + 5) = 12x.
Pour trouver le nombre choisi, il suffit donc de diviser le résultat par 12.
Cette démonstration confirme la conjecture.
Soit x le nombre choisi. Le programme s'écrit :
(x + 1)2 + (x + 2)2 − [(x − 1)2 − (x − 2)2] = x2 + 2x + 1 + x2 + 4x + 4 − (x2 − 2x + 1 + x2 − 4x + 4)
= 2x2 + 6x + 5 − (2x2 − 6x + 5) = 12x.
Pour trouver le nombre choisi, il suffit donc de diviser le résultat par 12.
Cette démonstration confirme la conjecture.
Remarque
Si la conjecture n'apparaît pas comme une évidence, commencez par la démonstration.Exercice 4
a) On passe du pentagone 1 au pentagone 2 par la rotation de centre A et d'angle 60°, dans le sens horaire.
b) On passe du pentagone 2 au pentagone 3 par la symétrie centrale de centre le milieu de [BC].
c) On passe du pentagone 3 au pentagone 4 par la translation envoyant C sur D (ou : translation de vecteur 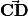 ).
).
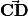 ).
).Troisième partie
Situation 1
1. Rôle et attendus de la première phase
La phase 1 permet de vérifier que les élèves ont compris l'enjeu de la situation, à savoir : placer chaque étiquette au même rang, à la même position, que l'étiquette correspondante sur le modèle. Cette phase introduit aussi ce qui sera ultérieurement un moyen de validation, en vérifiant que les élèves ont bien compris les critères de réussite.
Deux attendus pour cette phase sont donc :
La phase 1 permet de vérifier que les élèves ont compris l'enjeu de la situation, à savoir : placer chaque étiquette au même rang, à la même position, que l'étiquette correspondante sur le modèle. Cette phase introduit aussi ce qui sera ultérieurement un moyen de validation, en vérifiant que les élèves ont bien compris les critères de réussite.
Deux attendus pour cette phase sont donc :
- savoir repérer la position d'une image ;
- savoir placer une image à une position donnée.
Remarque
En fait, pour réussir, il suffit de placer une image directement en dessous de son modèle ; les attendus ne seront donc pas atteints s'il n'y a pas d'étayage langagier fort de la part de l'enseignante.2. Discussion autour des deux modèles de train proposés à la phase 2
Rappel
La capacité visée est : « utiliser le nombre pour repérer une position ».Le modèle 1 comporte trois motifs situés très près des extrémités pour deux d'entre eux : le carré est sur la 4e case à partir de la gauche et le point noir sur la 3e à partir de la droite. Le troisième motif est situé sur la 3e case à droite du carré. Les élèves peuvent donc percevoir globalement le nombre de cases vides entre deux éléments significatifs (extrémités ou images déjà positionnées).
Sur le modèle 2, les images sont plus éloignées des extrémités et les unes des autres. Le repérage des positions relatives passe forcément par le comptage : soit comptage/numérotage des cases, soit dénombrement par comptage de cases vides.
Sur le modèle 2, les images sont plus éloignées des extrémités et les unes des autres. Le repérage des positions relatives passe forcément par le comptage : soit comptage/numérotage des cases, soit dénombrement par comptage de cases vides.
3. Description des étapes de réalisation de la tâche
Pour réussir la tâche demandée dans la phase 2, un élève doit :
Pour réussir la tâche demandée dans la phase 2, un élève doit :
- 1. aller observer le train modèle ;
- 2. choisir un motif ;
- 3. repérer la position de ce motif sur le train modèle ;
- 4. mémoriser cette position ;
- 5. retourner à sa place ;
- 6. trouver l'étiquette comportant le même motif que celui choisi ;
- 7. trouver la case, sur le train personnel, se trouvant à la position repérée à l'étape 3 ;
- 8. placer le motif sur cette case ;
- 9. recommencer deux fois à partir de l'étape 1 (il n'y a plus de choix de motif possible à la dernière boucle).
4.
a) Description d'une procédure possible pour Sacha
Pour placer avec succès chacune des images du train modèle 2, Sacha peut dénombrer huit cases vides entre l'extrémité de gauche du modèle et le carré. Il va ensuite, sur son train, dénombrer huit cases à partir de la gauche, puis placer le carré directement après ces huit cases (vers la droite). Ensuite, sur le modèle, il peut dénombrer quatre cases vides entre le carré et l'étoile puis, sur son train, dénombrer quatre cases directement à droite du carré et placer l'étoile sur la suivante.
Pour placer le rond noir, il va dénombrer les cases vides à partir de l'extrémité de droite (il y en a 6) et faire de même sur son train.
Pour placer avec succès chacune des images du train modèle 2, Sacha peut dénombrer huit cases vides entre l'extrémité de gauche du modèle et le carré. Il va ensuite, sur son train, dénombrer huit cases à partir de la gauche, puis placer le carré directement après ces huit cases (vers la droite). Ensuite, sur le modèle, il peut dénombrer quatre cases vides entre le carré et l'étoile puis, sur son train, dénombrer quatre cases directement à droite du carré et placer l'étoile sur la suivante.
Pour placer le rond noir, il va dénombrer les cases vides à partir de l'extrémité de droite (il y en a 6) et faire de même sur son train.
b) Validation possible
Sacha peut savoir s'il a réussi en rapprochant son train du modèle, alignant verticalement les extrémités, puis en effectuant une correspondance terme à terme, cette procédure de vérification ayant été introduite à la phase 1.
Sacha peut savoir s'il a réussi en rapprochant son train du modèle, alignant verticalement les extrémités, puis en effectuant une correspondance terme à terme, cette procédure de vérification ayant été introduite à la phase 1.
Situation 2
Remarque
Analysons succinctement le problème rapidement avant de commencer : il s'agit d'un problème de distribution équitable, relevant de la structure « proportionnalité simple avec connaissance de l'unité » dans le sens de la multiplication, pour les deux questions.La première question est cependant triviale et ne nécessite pas d'effectuer une opération.
La seconde se résout de manière savante par la multiplication 4 × 18, mais des enfants de fin de CE1 ne disposent pas de connaissances suffisantes pour effectuer cette multiplication.
Les élèves devraient donc rester dans le champ additif, au moins pour la partie « calcul ».
1. Analyse de productions
a) Points communs et différences entre les procédures de Maëlys et de Malyan
• Points communs
- Les deux productions utilisent un dessin sur lequel est matérialisée la totalité des bonbons.
- Les bonbons sont représentés par des cercles.
- La quantité de bonbons est obtenue par comptage.
• Différences
- Maëlys traite directement dans le domaine numérique la distribution de gâteaux, alors que Malyan la matérialise par 18 cercles.
- Maëlys tente d'abord de traiter tout le problème dans le domaine numérique (on voit une addition en ligne barrée) avant d'opter pour une schématisation et un dénombrement par comptage.
- Maëlys distribue d'abord un bonbon à chaque élève, et fait 4 tours de distributions, matérialisés par 4 lignes de 18 cercles, consciencieusement numérotés, alors que Malyan distribue 4 bonbons à chacun des 18 élèves, ce qui est matérialisé par 18 paquets de 4 cercles.
- Maëlys rend visible son comptage par des chiffres, alors que Malyan compte probablement dans sa tête, on ne voit que le résultat du comptage.
b) Points communs et différences entre les procédures de Bérénice et de Mila
• Points communs
- Les deux productions modélisent le problème de la distribution de bonbons par une multiplication : 18 × 4.
- Les deux productions se passent d'une schématisation.
• Différences
- Bérénice modélise la distribution de gâteaux par une multiplication (18 × 1), alors que Mila se contente de donner le résultat sans commentaires.
- Bérénice traduit la multiplication par une addition itérée (18 + 18 + 18 + 18) qu'elle effectue (correctement) en la posant, tandis que Mila effectue bien la multiplication en s'appuyant sur la distributivité (18 × 4 = 10 × 4 + 8 × 4) et des faits numériques mémorisés (10 × 4 = 40 et 8 × 4 = 32).
2. Influencer la production de Martin
Martin modélise la distribution de bonbons par une addition itérée (et non par une multiplication) de 18 fois 4 gâteaux.
18 est déjà un grand nombre d'itérations, mais Martin est malin, et il la transforme en 9 fois 8, ce qui lui permet de rester dans un domaine numérique familier, voire mémorisé (la table de 8).
Proposer 32 à la place de 18 devrait obliger Martin à sortir de sa zone de confort (même en groupant par 8, cela ferait 16 fois 8) et à modifier sa stratégie.
Martin modélise la distribution de bonbons par une addition itérée (et non par une multiplication) de 18 fois 4 gâteaux.
18 est déjà un grand nombre d'itérations, mais Martin est malin, et il la transforme en 9 fois 8, ce qui lui permet de rester dans un domaine numérique familier, voire mémorisé (la table de 8).
Proposer 32 à la place de 18 devrait obliger Martin à sortir de sa zone de confort (même en groupant par 8, cela ferait 16 fois 8) et à modifier sa stratégie.
3. Une propriété de la multiplication
Maëlys a représenté la distribution de bonbons par ce que l'on a coutume d'appeler une « configuration rectangulaire ».
Celle-ci illustre la commutativité de la multiplication : selon que l'on regarde le rectangle dans le sens de la longueur ou de la largeur, on y voit, au choix :
Maëlys a représenté la distribution de bonbons par ce que l'on a coutume d'appeler une « configuration rectangulaire ».
Celle-ci illustre la commutativité de la multiplication : selon que l'on regarde le rectangle dans le sens de la longueur ou de la largeur, on y voit, au choix :
- 4 lignes de 18 cercles, soit 4 fois 18 cercles, soit encore 18 + 18 + 18 + 18, ce qui correspond au calcul de Bérénice ;
- 18 colonnes de 4 cercles, soit 18 fois 4 cercles, soit encore 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4, ce qui correspond au calcul de Martin.
Remarque
Notons que tant que Martin n'aura pas modélisé le problème par une multiplication, il ne pourra pas utiliser cette propriété de commutativité, qui n'a pas posé de problème à Bérénice.Situation 3
1. « Dans un nombre, à quoi sert la virgule ? »
Remarque
Commençons par noter que la question de l'enseignant est maladroite, car la virgule n'est pas « dans un nombre », mais fait éventuellement partie de l'écriture d'un nombre.Il eût été plus pertinent de demander « Dans l'écriture décimale d'un nombre, que signifie la présence de la virgule ? »
a) Critique des réponses des élèves
Élève A : « La virgule sert à montrer que c'est un nombre décimal. »
Cette réponse, intéressante car elle relie avec raison la virgule à la notion de nombre décimal, ne permet pas d'englober les nombres entiers parmi les nombres décimaux, ni à comprendre que les nombres décimaux peuvent s'écrire autrement qu'avec une virgule (par une fraction décimale, par exemple).
Élève B : « La virgule sert à séparer le nombre entier et la partie décimale. »
Cette réponse contribue à concevoir un nombre décimal comme la juxtaposition de deux entiers, conception dont on sait qu'elle est source d'erreur. Par ailleurs, elle est fausse car la virgule ne sépare pas le nombre entier et la partie décimale, celle-ci n'étant pas exclusivement composée des chiffres écrits à droite de la virgule. Ex. : pour 12,35 le « nombre entier » (ou plutôt : la partie entière) est 12, mais la partie décimale est 0,35.
Élève A : « La virgule sert à montrer que c'est un nombre décimal. »
Cette réponse, intéressante car elle relie avec raison la virgule à la notion de nombre décimal, ne permet pas d'englober les nombres entiers parmi les nombres décimaux, ni à comprendre que les nombres décimaux peuvent s'écrire autrement qu'avec une virgule (par une fraction décimale, par exemple).
Élève B : « La virgule sert à séparer le nombre entier et la partie décimale. »
Cette réponse contribue à concevoir un nombre décimal comme la juxtaposition de deux entiers, conception dont on sait qu'elle est source d'erreur. Par ailleurs, elle est fausse car la virgule ne sépare pas le nombre entier et la partie décimale, celle-ci n'étant pas exclusivement composée des chiffres écrits à droite de la virgule. Ex. : pour 12,35 le « nombre entier » (ou plutôt : la partie entière) est 12, mais la partie décimale est 0,35.
b) Réponse proposée par l'enseignant
« Dans l'écriture décimale d'un nombre, la virgule sert à marquer la position de l'unité. Lorsque le nombre n'est pas entier, on écrit une virgule immédiatement à droite du chiffre des unités. »
« Dans l'écriture décimale d'un nombre, la virgule sert à marquer la position de l'unité. Lorsque le nombre n'est pas entier, on écrit une virgule immédiatement à droite du chiffre des unités. »
Remarque
On pourrait rappeler également que, comme le chiffre zéro, la virgule est un marqueur de l'écrit, et qu'elle peut/doit ne pas être prononcée à l'oral.2. Calcul d'un périmètre
a) Analyse de la production d'un élève
Pour calculer le périmètre de la figure, l'élève sait qu'il faut additionner les mesures des longueurs de chacun des côtés.
Il choisit d'additionner d'abord les parties entières des mesures de chaque côté, lorsque celles-ci étaient explicites. Il ne prend pas en compte celle de la mesure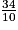 .
.
Le résultat de ce premier calcul, 9, effectué mentalement, est correct.
Il additionne ensuite les dixièmes restants de chaque mesure en écriture fractionnaire, en convertissant l'écriture décimale 0,5 en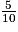 .
.
Curieusement, le résultat de ce second calcul,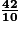 , omet de prendre en compte ces
, omet de prendre en compte ces 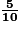 . Il est donc incorrect.
. Il est donc incorrect.
Obtenant 9 à son premier calcul, et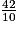 au second, il en conclut que la mesure du périmètre est 9,42 ; ce qui est évidemment incorrect. Il omet de convertir 40 dixièmes en 4 unités.
au second, il en conclut que la mesure du périmètre est 9,42 ; ce qui est évidemment incorrect. Il omet de convertir 40 dixièmes en 4 unités.
Pour calculer le périmètre de la figure, l'élève sait qu'il faut additionner les mesures des longueurs de chacun des côtés.
Il choisit d'additionner d'abord les parties entières des mesures de chaque côté, lorsque celles-ci étaient explicites. Il ne prend pas en compte celle de la mesure
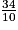 .
.Le résultat de ce premier calcul, 9, effectué mentalement, est correct.
Il additionne ensuite les dixièmes restants de chaque mesure en écriture fractionnaire, en convertissant l'écriture décimale 0,5 en
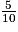 .
.Curieusement, le résultat de ce second calcul,
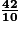 , omet de prendre en compte ces
, omet de prendre en compte ces 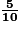 . Il est donc incorrect.
. Il est donc incorrect.Obtenant 9 à son premier calcul, et
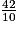 au second, il en conclut que la mesure du périmètre est 9,42 ; ce qui est évidemment incorrect. Il omet de convertir 40 dixièmes en 4 unités.
au second, il en conclut que la mesure du périmètre est 9,42 ; ce qui est évidemment incorrect. Il omet de convertir 40 dixièmes en 4 unités.b) Proposition pour aider l'élève à corriger ses erreurs
La seule erreur véritable est l'interprétation de l'écriture 9,42 en 9 et 42 dixièmes.
Il s'agit donc d'un problème de conversion entre les deux registres de l'écriture décimale et de l'écriture fractionnaire.
Plusieurs possibilités s'offrent pour aider l'élève, la première consistant à lui demander de verbaliser l'écriture 9,42 : « 9 unités 4 dixièmes et 2 centièmes, ou 9 unités et 42 centièmes » et de comparer avec la verbalisation de 9 et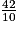 , soit « 9 unités et 42 dixièmes ».
, soit « 9 unités et 42 dixièmes ».
On peut par ailleurs :
La seule erreur véritable est l'interprétation de l'écriture 9,42 en 9 et 42 dixièmes.
Il s'agit donc d'un problème de conversion entre les deux registres de l'écriture décimale et de l'écriture fractionnaire.
Plusieurs possibilités s'offrent pour aider l'élève, la première consistant à lui demander de verbaliser l'écriture 9,42 : « 9 unités 4 dixièmes et 2 centièmes, ou 9 unités et 42 centièmes » et de comparer avec la verbalisation de 9 et
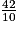 , soit « 9 unités et 42 dixièmes ».
, soit « 9 unités et 42 dixièmes ».On peut par ailleurs :
- (faire) matérialiser 9 et 42 dixièmes à l'aide de matériel de numération, (faire) réaliser les conversions « dix dixièmes égalent une unité » et (faire) lire/écrire le résultat obtenu ;
- et/ou convoquer un autre registre, celui de la droite graduée, en faisant placer 9 et 42 dixièmes sur une droite graduée en dixièmes et unités par comptage de 42 dixièmes « après 9 », puis en faisant (re)lire le résultat (13 et 2 dixièmes) pour finalement en proposer l'écriture décimale.
Document précédent
Sujet 2020, groupement académique 2
Document suivant
Sujet 2019, groupement académique 1
