Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
Mme Martin souhaite participer à l'effort de protection de la planète et s'engager dans le développement durable.
Elle a décidé d'installer des panneaux photovoltaïques, sur le toit de sa maison, pour produire sa propre énergie électrique ainsi qu'un récupérateur d'eau de pluie pour arroser son jardin.
Elle a décidé d'installer des panneaux photovoltaïques, sur le toit de sa maison, pour produire sa propre énergie électrique ainsi qu'un récupérateur d'eau de pluie pour arroser son jardin.
A. Installation de panneaux photovoltaïques
Le toit de la maison de Mme Martin a la forme d'un trapèze rectangle ABCD représenté ci-dessous pour lequel on connaît les dimensions suivantes :
- AB = 8 m ;
- AD = 7 m ;
- CB = 3 m.
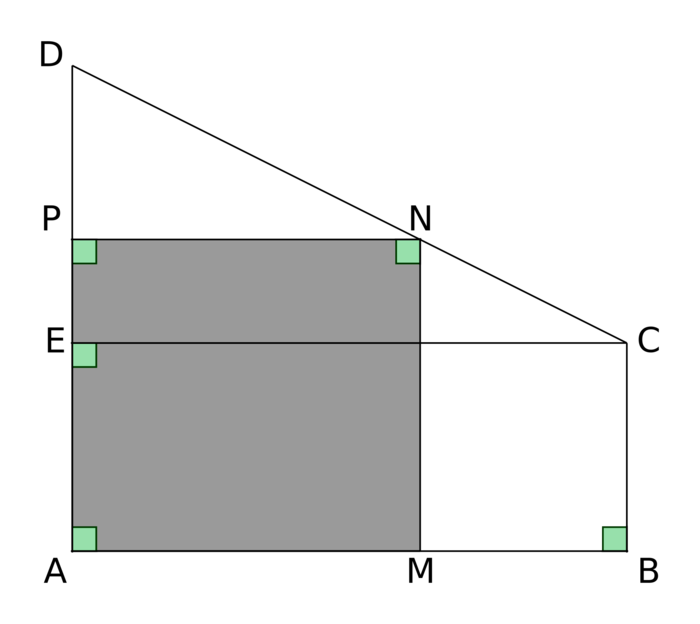 |
Le point E est le point de [AD] tel que ABCE soit un rectangle.
Le support dédié aux panneaux photovoltaïques correspond au rectangle AMNP où P est un point situé sur [DE] et N est l'intersection de la droite perpendiculaire à (AD) passant par P avec (CD).
On souhaite déterminer la position du point P sur [DE] pour que l'aire du support AMNP soit la plus grande possible.
On note x la longueur du segment [DP] exprimée en mètres et A(x) l'aire du rectangle AMNP exprimée en mètres carrés.
Le support dédié aux panneaux photovoltaïques correspond au rectangle AMNP où P est un point situé sur [DE] et N est l'intersection de la droite perpendiculaire à (AD) passant par P avec (CD).
On souhaite déterminer la position du point P sur [DE] pour que l'aire du support AMNP soit la plus grande possible.
On note x la longueur du segment [DP] exprimée en mètres et A(x) l'aire du rectangle AMNP exprimée en mètres carrés.
1. Expliquer pourquoi x doit être compris entre 0 et 4.
2. Démontrer que PN est égale à 2x.
3. Montrer que, pour tout nombre x compris entre 0 et 4, on a : A(x) = 14x − 2x2.
4. Calculer l'aire du support, en mètres carrés, si l'on choisit x = 2.
5. Le graphique ci-dessous représente l'aire du support, en mètres carrés, en fonction de la longueur x en mètres.
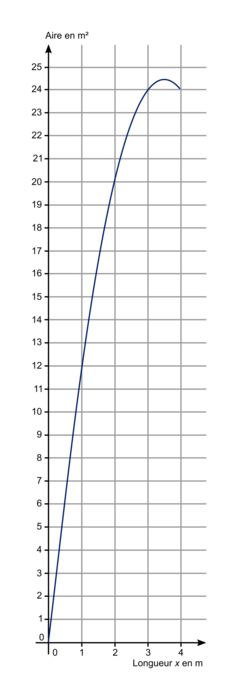 |
Répondre par lecture graphique aux questions suivantes :
a) Quelle est l'aire, en mètres carrés, du support si la longueur x est égale à 3 m ?
b) Pour quelle(s) valeur(s) de la longueur x, l'aire du support est-elle égale à 12 m2 ?
c) Pour quelle valeur de la longueur x, l'aire du support est-elle maximale ?
B. Les différentes énergies renouvelables
Les informations présentées dans cette partie sont extraites du site « RTE, Réseau de transport d'électricité ».
Le tableau ci-dessous indique la production française d'énergie électrique renouvelable par filière en 2017, exprimée en térawattheures (TWh).
| Filière | Production |
|---|---|
| Filière éolienne | 24 TWh |
| Filière solaire | 9,2 TWh |
| Filière hydraulique | 48,6 TWh |
| Filière des bioénergies | 7 TWh |
1. Calculer le pourcentage que représente l'énergie électrique produite par la filière solaire par rapport à l'énergie électrique produite par l'ensemble des filières des énergies renouvelables.
2. En 2017, l'électricité renouvelable a couvert 18,4 % de l'électricité consommée en France. Calculer la quantité totale d'électricité consommée en France en 2017. On donnera l'arrondi au dixième de térawattheure.
C. Coût de l'énergie électrique
Chaque matin, Mme Martin fait bouillir un demi-litre d'eau dans une bouilloire pour préparer son thé.
En utilisant les informations ci-dessous, calculer le prix de l'énergie électrique, toutes taxes comprises, utilisée par Mme Martin pour préparer son thé chaque matin durant toute l'année 2018.
En utilisant les informations ci-dessous, calculer le prix de l'énergie électrique, toutes taxes comprises, utilisée par Mme Martin pour préparer son thé chaque matin durant toute l'année 2018.
| Document 1 : Caractéristiques de la bouilloire électrique de Mme Martin Durée du chauffage pour 0,5 L d'eau : 1 min 26 s Puissance : 2 200 W |
| Document 2 : Énergie électrique E = P × t E désigne l'énergie en wattheures (Wh) P désigne la puissance en watts (W) t désigne le temps en heures (h) |
| Document 3 : Prix de l'énergie électrique Prix hors TVA d'un kilowattheure (kWh) : 0,0997 € TVA sur l'énergie électrique : 20 % |
D. Installation d'un récupérateur d'eau
Mme Martin choisit d'installer un récupérateur d'eau ayant la forme d'une pyramide à base rectangulaire tronquée, représentée par le solide ABCDA'B'C'D' sur le schéma ci-dessous qui n'est pas à l'échelle. Le plan (A'B'C') est parallèle au plan (ABC).
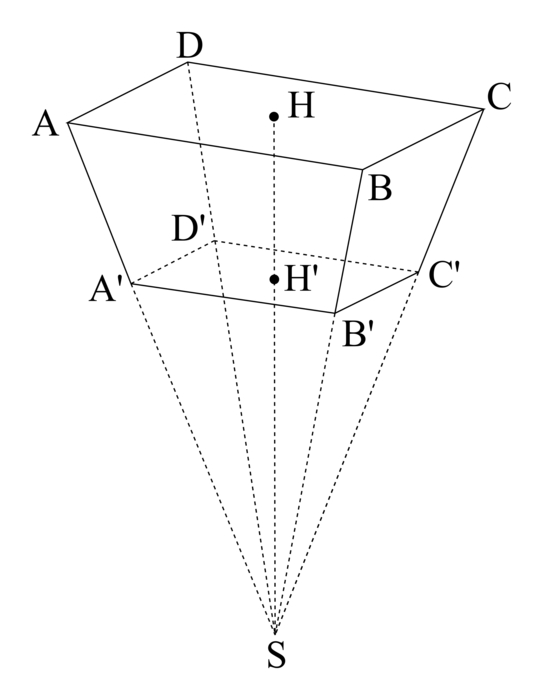 |
On donne les dimensions suivantes :
- AB = 1,9 m ;
- AD = 92 cm ;
- HH' = 1,84 m ;
- SH = 4,60 m.
1. Calculer le volume V1 de la pyramide SABCD, en mètres cubes, arrondi au litre.
| On rappelle la formule du volume d'une pyramide : V = 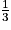 × aire de la base × hauteur × aire de la base × hauteur |
2.
a) Calculer le coefficient de réduction permettant de passer de la pyramide SABCD à la pyramide SA'B'C'D'.
b) En déduire le volume V2 de la pyramide SA'B'C'D', en mètres cubes, arrondi au litre.
3. Montrer que le volume V du récupérateur d'eau est environ égal à 2,101 m3.
4. Mme Martin possède un arrosoir d'une capacité de 12 litres.
Calculer le nombre d'arrosoirs qu'elle peut remplir complètement avec l'eau contenue dans son récupérateur plein.
Calculer le nombre d'arrosoirs qu'elle peut remplir complètement avec l'eau contenue dans son récupérateur plein.
Deuxième partie (13 points)
Cette partie est composée de quatre exercices indépendants.
Exercice 1
Pour gérer son parc d'éoliennes, un exploitant procède à des relevés de la vitesse du vent sur l'une d'entre elles. Durant l'année 2019, ces relevés ont été effectués toutes les minutes.
1. Combien de relevés ont été réalisés en 2019 ?
2. Le tableau suivant donne plusieurs résultats statistiques issus de ces relevés :
On précise qu'une éolienne de ce parc :
| Étendue | Médiane | Moyenne | Maximum |
|---|---|---|---|
| 23 m/s | 14,3 m/s | 13 m/s | 24 m/s |
On précise qu'une éolienne de ce parc :
- tourne dès que la vitesse du vent atteint 3 m/s ;
- a sa puissance électrique stabilisée dès que la vitesse du vent atteint 13 m/s ;
- s'arrête dès que la vitesse du vent est supérieure à 25 m/s.
a) Le gérant prétend que les éoliennes de son parc n'ont pas fonctionné continuellement durant l'année 2019. A-t-il raison ? Justifier.
b) Peut-il affirmer que les éoliennes ont délivré une puissance électrique stabilisée pendant au moins la moitié du temps ? Justifier.
Exercice 2
Indiquer si les affirmations suivantes sont vraies ou fausses en justifiant la réponse. Une réponse exacte mais non justifiée ne rapporte aucun point. Une réponse fausse, incorrecte ou une absence de réponse n'enlève pas de point.
1. Affirmation : « Le nombre 4 700 001 est un nombre premier. »
2. Affirmation : « Les nombres 3212 et 1615 + 3 sont égaux. »
3. Affirmation : « La somme des carrés de deux nombres entiers naturels consécutifs est toujours un nombre impair. »
4. Affirmation : « Le triangle ABC avec AB = 6,4 m, BC = 4,8 m et AC = 8 m est rectangle en B. »
Exercice 3
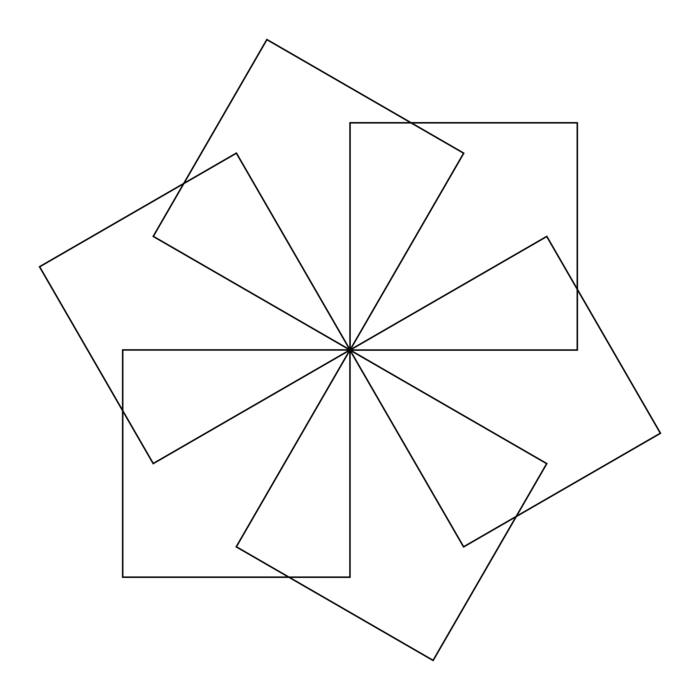 |
Pour réaliser la rosace ci-dessus, on a défini un motif « Carré » et on a utilisé le programme ci-dessous.
 |
1. Combien de motifs « Carré » composent la rosace ?
2. Quelle transformation géométrique permet de passer d'un motif « Carré » au motif « Carré » suivant ?
3. Clément souhaite modifier le programme pour que la rosace soit composée de 10 motifs comme ci-dessous.
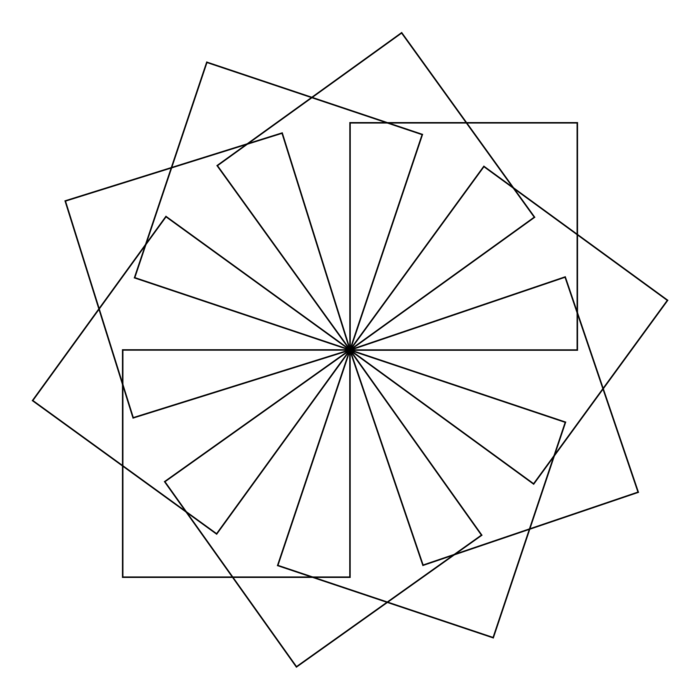 |
Quelles modifications doit-il apporter au programme ?
4. Iness souhaite obtenir la figure ci-dessous où chaque motif est espacé de 10 pixels.
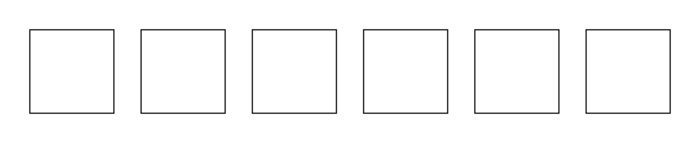 |
Par quelle instruction doit-elle remplacer l'instruction « tourner de 60 degrés » pour obtenir cette nouvelle figure ?
Exercice 4
Kelly et Mourad ont chacun un dé cubique équilibré. Les faces de leurs dés sont soit rouges, soit bleues. Le dé de Mourad a 5 faces rouges et 1 face bleue.
Chacun lance son dé.
Chacun lance son dé.
- Si les deux faces supérieures sont de la même couleur, alors c'est Mourad qui gagne.
- Si les deux faces supérieures sont de couleurs différentes, alors c'est Kelly qui gagne.
1.
Kelly propose de colorier 4 faces de son dé en rouge et 2 en bleu.
a) Démontrer que la probabilité que Mourad gagne est égale à 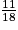 .
.
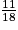 .
.b) Le coloriage proposé permet-il de répondre affirmativement à la question que Kelly et Mourad se posent ? Justifier.
2.
On appelle x le nombre de faces coloriées en rouge sur le dé de Kelly.
a) Montrer que la probabilité que Mourad gagne est égale à 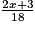 .
.
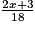 .
.b) Déterminer la valeur de x pour répondre à la question que Kelly et Mourad se posent.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Voici un extrait de la note de service n° 2018-052 du 25 avril 2018 « La résolution de problèmes à l'école élémentaire ».
« Modéliser » et « calculer » sont deux compétences fondamentales pour la résolution de problèmes à l'école élémentaire qui doivent guider l'action de l'enseignant pour aider les élèves à surmonter leurs difficultés. En effet, lors de la résolution de problèmes, les principales difficultés rencontrées peuvent relever de :
|
Un enseignant propose à ses élèves de CE1 le problème suivant issu d'une évaluation nationale de 2012 (DEPP) :
| « L'album de Rémi et Chloé peut contenir 100 photos. Rémi veut ranger 24 photos et Chloé 16. Combien de places restera-t-il pour de nouvelles photos ? ». |
Voici les réponses proposées par 5 élèves :
Élève A
 |
Élève B
 |
Élève C
24 + 16 = 40
100 − 40 = 60
60 places
24 + 16 = 40
100 − 40 = 60
60 places
Élève D
100 − 24 = 76 − 16 = 60
Il y a encore 60 places.
100 − 24 = 76 − 16 = 60
Il y a encore 60 places.
Élève E
24 − 16 = 8
Réponse = 8
24 − 16 = 8
Réponse = 8
1. En s'appuyant sur l'extrait de la note de service proposé ci-dessus, analyser les cinq propositions d'élèves en termes de réussites et d'échecs pour chacune des compétences « modéliser » et « calculer ».
2. Proposer deux activités de remédiation que l'on pourrait envisager pour aider l'élève A à réussir ce type de problème, une avec du matériel et une sans matériel.
3. Proposer une activité de remédiation que l'on pourrait envisager pour aider l'élève B à comprendre son erreur.
4. On considère maintenant le problème suivant : « L'album de Rémi peut contenir 100 photos. Rémi veut ranger 24 photos. Combien de places restera-t-il pour de nouvelles photos ? »
En proposant ce second problème à la place du problème initial, quelles erreurs risqueraient de ne pas être détectées ? En citer deux.
En proposant ce second problème à la place du problème initial, quelles erreurs risqueraient de ne pas être détectées ? En citer deux.
Situation 2
Un enseignant d'une classe de CM2 propose l'exercice suivant à ses élèves :
| L'aire d'un rectangle est de 16 cm2. Trouve une longueur et une largeur possibles pour ce rectangle. Quel est alors son périmètre ? Cherche le plus de solutions possible. |
1. Citer au moins deux notions qu'un élève doit avoir travaillées pour pouvoir résoudre le problème ci-dessus.
2. Proposer quatre couples de réponses (longueur et largeur du rectangle, avec une longueur supérieure ou égale à la largeur) attendus d'un élève de CM2 aux deux premières questions.
3. Citer au moins deux difficultés qu'un élève peut rencontrer pour déterminer des couples de solutions.
4. Un élève propose comme couple de solutions les longueurs 4 cm et 4 cm. Un de ses camarades lui dit : « Ta solution est fausse, car la figure est un carré. »
Proposer des éléments que l'enseignant peut apporter à ces deux élèves pour les aider à trancher.
Proposer des éléments que l'enseignant peut apporter à ces deux élèves pour les aider à trancher.
5. Un autre élève, qui a effectué la division ci-dessous, propose comme couple de solutions les longueurs 5,33 cm et 3 cm.
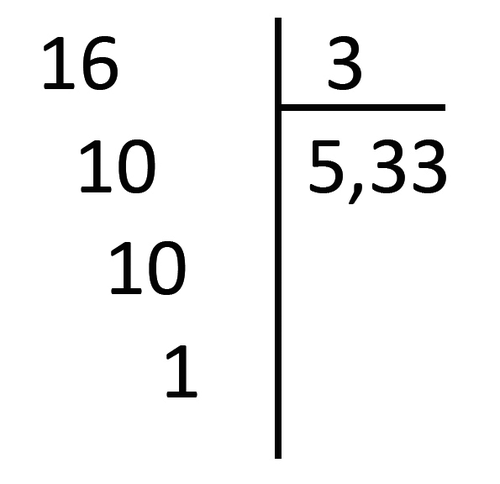 |
a) Faire une hypothèse sur le raisonnement que l'élève a conduit pour proposer ce résultat.
b) Que révèle cette procédure sur les acquis de l'élève ?
c) Comment montrer à cet élève que cette réponse ne convient pas ?
d) Quelle exploitation l'enseignant pourrait-il faire en classe de cette proposition ?
Situation 3
Un enseignant propose à ses élèves de CM2 l'exercice suivant.
| Dans le livre de recettes de cuisine de Corentin, on donne la recette pour faire 15 crêpes ou 25 crêpes : Pour 15 crêpes
Donne la quantité d'ingrédients nécessaires pour faire 10 crêpes. Mme Lucas veut préparer 60 crêpes pour la fête d'anniversaire de sa fille. Elle a emprunté le livre de recettes de Corentin. Quelles sont les quantités d'ingrédients nécessaires pour faire 60 crêpes ? |
1. Quelle est la principale notion du programme travaillée dans cet exercice ?
2. Analyser le choix des nombres de crêpes dans cet exercice.
3. Expliciter trois procédures correctes attendues des élèves pour calculer la masse de farine pour 10 crêpes.
4. Pour cette question, la production d'un élève est proposée ci-dessous :
 |
Relever la ou les erreurs rencontrées et proposer une aide possible pour chacune d'entre elles.
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Installation de panneaux photovoltaïques
Remarque
x et A(x) sont des nombres et non des grandeurs ; il faudrait donc, non pas dire « x la longueur du segment [DP] exprimée en mètres », mais « x la mesure de la longueur DP, exprimée en mètres ».De même, A(x) est la mesure de l'aire de AMNP, exprimée en mètres carrés, et non l'aire elle-même.
1. Valeurs possibles pour x
Le point P étant sur le segment [DE], la longueur DP est comprise entre la longueur nulle DD et la longueur DE.
Or, DE = DA − EA, puisque E est un point du segment [AD].
Et EA = BC puisque ABCE est un rectangle.
Donc DE = 7 m − 3 m = 4 m.
On en conclut que x, la mesure de DP en mètres, est compris entre 0 et 4.
Le point P étant sur le segment [DE], la longueur DP est comprise entre la longueur nulle DD et la longueur DE.
Or, DE = DA − EA, puisque E est un point du segment [AD].
Et EA = BC puisque ABCE est un rectangle.
Donc DE = 7 m − 3 m = 4 m.
On en conclut que x, la mesure de DP en mètres, est compris entre 0 et 4.
2. Expression de PN
Le triangle DNP est une réduction du triangle DEC puisque les droites (PN) et (EC), étant toutes deux perpendiculaires à (AD), sont parallèles entre elles.
Le coefficient de réduction est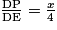 .
.
PN étant la longueur réduite correspondant à EC, on a :
PN =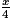 EC =
EC = 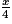 × 8 m = 2x m.
× 8 m = 2x m.
La mesure de PN en mètres est donc 2x.
Le triangle DNP est une réduction du triangle DEC puisque les droites (PN) et (EC), étant toutes deux perpendiculaires à (AD), sont parallèles entre elles.
Le coefficient de réduction est
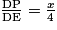 .
.PN étant la longueur réduite correspondant à EC, on a :
PN =
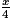 EC =
EC = 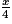 × 8 m = 2x m.
× 8 m = 2x m.La mesure de PN en mètres est donc 2x.
3. Expression de A(x)
AMNP étant un rectangle, son aire est AP × PN.
Or, on a vu à la question précédente que PN = 2x m.
De plus, P étant sur le segment [AD], AP = AD − DP = 7 m − x m = (7 − x) m.
A(x) étant la mesure en mètres carrés de l'aire de AMNP, on a :
A(x) = 2x × (7 − x) = 14x − 2x2.
AMNP étant un rectangle, son aire est AP × PN.
Or, on a vu à la question précédente que PN = 2x m.
De plus, P étant sur le segment [AD], AP = AD − DP = 7 m − x m = (7 − x) m.
A(x) étant la mesure en mètres carrés de l'aire de AMNP, on a :
A(x) = 2x × (7 − x) = 14x − 2x2.
4. Aire du support si x = 2
A(2) = 14 × 2 − 2 × 22 = 28 − 2 × 4 = 28 − 8 = 20.
Pour x = 2, la mesure de l'aire en mètres carrés est 20.
A(2) = 14 × 2 − 2 × 22 = 28 − 2 × 4 = 28 − 8 = 20.
Pour x = 2, la mesure de l'aire en mètres carrés est 20.
5.
a) Aire du support si x = 3
Pour x = 3, l'aire a pour mesure en mètres carrés environ 24.
Pour x = 3, l'aire a pour mesure en mètres carrés environ 24.
b) Valeur(s) de x pour une aire de support égale à 12 m2
Une aire de 12 m2 correspond à une valeur de x égale à environ 1.
Une aire de 12 m2 correspond à une valeur de x égale à environ 1.
c) Valeur de x pour une aire de support maximale
La valeur maximale de la mesure de l'aire correspond à une valeur de x environ égale à 3,5.
La valeur maximale de la mesure de l'aire correspond à une valeur de x environ égale à 3,5.
B. Les différentes énergies renouvelables
1. Pourcentage que représente l'énergie solaire par rapport à l'ensemble des énergies renouvelables
Calculons la production totale de la filière renouvelable pour l'année 2017, en TWh :
24 + 9,2 + 48,6 + 7 = 88,8.
La filière solaire a produit 9,2 TWh en 2017, soit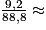 0,1036.
0,1036.
La filière solaire représente environ 10,4 % de la filière du renouvelable.
Calculons la production totale de la filière renouvelable pour l'année 2017, en TWh :
24 + 9,2 + 48,6 + 7 = 88,8.
La filière solaire a produit 9,2 TWh en 2017, soit
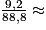 0,1036.
0,1036.La filière solaire représente environ 10,4 % de la filière du renouvelable.
2. Quantité totale d'électricité consommée en France en 2017
Les 88,8 TWh produit par les filières renouvelables en 2017 représentent 18,4 % de l'énergie électrique totale consommée en France en 2017.
Si nous notons E cette énergie en TWh, alors :
88,8 = E ×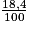 = 0,184E.
= 0,184E.
Donc E =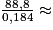 482,6.
482,6.
En 2017, la consommation d'électricité en France a été de 482,6 TWh environ.
Les 88,8 TWh produit par les filières renouvelables en 2017 représentent 18,4 % de l'énergie électrique totale consommée en France en 2017.
Si nous notons E cette énergie en TWh, alors :
88,8 = E ×
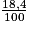 = 0,184E.
= 0,184E.Donc E =
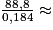 482,6.
482,6.En 2017, la consommation d'électricité en France a été de 482,6 TWh environ.
C. Coût de l'énergie électrique
Commençons par calculer l'énergie électrique consommée par Mme Martin chaque matin :Ematin = P × t avec :
- P = 2 200 W ;
- t = 1 min 26 s = 86 s =
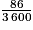 h.
h.
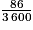 Wh =
Wh = 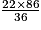 Wh =
Wh = 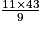 Wh =
Wh = 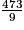 Wh
Wh  53 Wh.
53 Wh.Calculons maintenant l'énergie électrique consommée sur une année entière :
L'année 2018 n'étant pas une année bissextile, elle se compose de 365 jours, donc 365 matins.
Donc, Eannée 2018 =
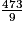 × 365 Wh
× 365 Wh  19 183 Wh
19 183 Wh  19 kWh.
19 kWh.Il reste à calculer le prix de cette énergie consommée :
Prix = 19,183 × 0,0997 × 1,2
 2,295 €.
2,295 €.L'énergie électrique consommée par le thé de Mme Martin lui a coûté environ 2,30 € pour l'année 2018.
D. Installation d'un récupérateur d'eau
1. Volume de la pyramide
Soit V1, le volume de la pyramide SABCD.
V1 =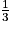 × AB × AD × SH.
× AB × AD × SH.
V1 =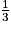 × (1,9 m) × (0,92 m) × (4,6 m).
× (1,9 m) × (0,92 m) × (4,6 m).
V1 2,6802667 m3.
2,6802667 m3.
Le volume de SABCD est donc d'environ 2,680 m3.
Soit V1, le volume de la pyramide SABCD.
V1 =
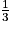 × AB × AD × SH.
× AB × AD × SH.V1 =
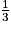 × (1,9 m) × (0,92 m) × (4,6 m).
× (1,9 m) × (0,92 m) × (4,6 m).V1
 2,6802667 m3.
2,6802667 m3.Le volume de SABCD est donc d'environ 2,680 m3.
Remarque
La formulation de la réponse « 2,680 m3 » et non « 2,68 m3 » permet de rendre explicite l'arrondi au litre près.2.
a) Coefficient de réduction pour passer de SABCD à SA'B'C'D'
La hauteur SH de la grande pyramide est réduite en la hauteur SH' de la petite.
Or, SH' = SH − HH', puisque S, H' et H sont alignés dans cet ordre.
Ainsi, SH' = 4,60 m − 1,84 m = 2,76 m.
Le coefficient de réduction k =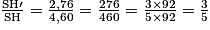 = 0,6.
= 0,6.
La hauteur SH de la grande pyramide est réduite en la hauteur SH' de la petite.
Or, SH' = SH − HH', puisque S, H' et H sont alignés dans cet ordre.
Ainsi, SH' = 4,60 m − 1,84 m = 2,76 m.
Le coefficient de réduction k =
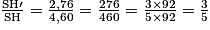 = 0,6.
= 0,6.b) Volume de SA'B'C'D'
Comme les longueurs sont multipliées par k = 0,6, les volumes sont multipliés par k3 = 0,63.
Ainsi, V2 = V1 × (0,6)3 2,6802667 × 0,216
2,6802667 × 0,216  0,578938 m3.
0,578938 m3.
Le volume de la pyramide réduite SA'B'C'D' est d'environ 0,579 m3.
Comme les longueurs sont multipliées par k = 0,6, les volumes sont multipliés par k3 = 0,63.
Ainsi, V2 = V1 × (0,6)3
 2,6802667 × 0,216
2,6802667 × 0,216  0,578938 m3.
0,578938 m3.Le volume de la pyramide réduite SA'B'C'D' est d'environ 0,579 m3.
3. Volume du récupérateur d'eau
V = V1 − V2 2,680 m3 − 0,579 m3 = 2,101 m3.
2,680 m3 − 0,579 m3 = 2,101 m3.
V = V1 − V2
 2,680 m3 − 0,579 m3 = 2,101 m3.
2,680 m3 − 0,579 m3 = 2,101 m3.4. Nombre d'arrosoirs correspondants
Si le récupérateur d'eau est plein, alors d'après la question précédente il contient environ 2 101 litres d'eau.
Un arrosoir contient 12 litres d'eau. D'où :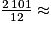 175,08.
175,08.
À raison de 12 litres d'eau par arrosoir, cela fait environ 175 arrosoirs que l'on peut remplir.
Si le récupérateur d'eau est plein, alors d'après la question précédente il contient environ 2 101 litres d'eau.
Un arrosoir contient 12 litres d'eau. D'où :
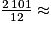 175,08.
175,08.À raison de 12 litres d'eau par arrosoir, cela fait environ 175 arrosoirs que l'on peut remplir.
Deuxième partie
Exercice 1
1. Nombre de relevés réalisés en 2019
2019 n'est pas une année bissextile.
1 an = 365 jours = 365 × 24 h = 365 × 24 × 60 min = 525 600 min.
On a réalisé 525 600 relevés en 2019.
2019 n'est pas une année bissextile.
1 an = 365 jours = 365 × 24 h = 365 × 24 × 60 min = 525 600 min.
On a réalisé 525 600 relevés en 2019.
2.
a) Les éoliennes ont-elles fonctionné continuellement ?
La vitesse du vent maximale relevée est de 24 m/s et l'étendue de la série statistique est 23 m/s. La vitesse minimale relevée est donc : 24 m/s − 23 m/s = 1 m/s.
Comme les éoliennes ne tournent pas si la vitesse du vent est inférieure à 3 m/s, on en déduit que les éoliennes n'ont pas tourné continuellement.
Le gérant a raison.
La vitesse du vent maximale relevée est de 24 m/s et l'étendue de la série statistique est 23 m/s. La vitesse minimale relevée est donc : 24 m/s − 23 m/s = 1 m/s.
Comme les éoliennes ne tournent pas si la vitesse du vent est inférieure à 3 m/s, on en déduit que les éoliennes n'ont pas tourné continuellement.
Le gérant a raison.
b) Durée de délivrance d'une puissance électrique stabilisée
La médiane a été établie à 14,3 m/s ; cela signifie qu'au moins la moitié du temps la vitesse du vent a été supérieure à 14,3 m/s. Or, la puissance des éoliennes est stabilisée dès lors que la vitesse du vent est supérieure ou égale à 13 m/s.
On en déduit que les éoliennes ont délivré une puissance électrique stabilisée au moins la moitié du temps.
La médiane a été établie à 14,3 m/s ; cela signifie qu'au moins la moitié du temps la vitesse du vent a été supérieure à 14,3 m/s. Or, la puissance des éoliennes est stabilisée dès lors que la vitesse du vent est supérieure ou égale à 13 m/s.
On en déduit que les éoliennes ont délivré une puissance électrique stabilisée au moins la moitié du temps.
Exercice 2
1. 4 + 7 + 1 = 12 = 4 × 3.
4 700 001 est divisible par 3 et ne peut donc pas être premier.
L'affirmation 1 est fausse.
4 700 001 est divisible par 3 et ne peut donc pas être premier.
L'affirmation 1 est fausse.
2. 3212 est un nombre pair.
1615 + 3 est la somme d'un nombre pair et d'un nombre impair : il est donc impair.
Ces deux nombres ne peuvent donc être égaux.
L'affirmation 2 est fausse.
1615 + 3 est la somme d'un nombre pair et d'un nombre impair : il est donc impair.
Ces deux nombres ne peuvent donc être égaux.
L'affirmation 2 est fausse.
Remarque
On pouvait aussi écrire :3212 = (2 × 16)12 = 212 × 1612 = (24)3 × 1612 = 163 × 1612 = 1615 et conclure.
3.
• Résultats préliminaires :
Deux entiers naturels consécutifs sont, l'un pair, l'autre impair. D'après les résultats préliminaires, la somme des carrés de deux nombres consécutifs est donc la somme d'un nombre pair et d'un nombre impair ; cette somme est impaire.
L'affirmation 3 est vraie.
- le carré d'un nombre pair est pair ;
- le carré d'un nombre impair est impair.
Deux entiers naturels consécutifs sont, l'un pair, l'autre impair. D'après les résultats préliminaires, la somme des carrés de deux nombres consécutifs est donc la somme d'un nombre pair et d'un nombre impair ; cette somme est impaire.
L'affirmation 3 est vraie.
• Autre méthode :
Soit n un nombre entier quelconque.
Alors, on peut traduire algébriquement l'expression : « la somme des carrés de deux nombres entiers consécutifs » par : n2 + (n + 1)2.
On a : n2 + (n + 1)2 = n2 + n2 + 2n + 1 = 2n2 + 2n + 1 = 2(n2 + n) + 1 = 2N + 1, où N = n2 + n est un nombre entier naturel.
2N + 1 est le successeur d'un nombre pair, il est donc impair.
L'affirmation 3 est vraie.
Soit n un nombre entier quelconque.
Alors, on peut traduire algébriquement l'expression : « la somme des carrés de deux nombres entiers consécutifs » par : n2 + (n + 1)2.
On a : n2 + (n + 1)2 = n2 + n2 + 2n + 1 = 2n2 + 2n + 1 = 2(n2 + n) + 1 = 2N + 1, où N = n2 + n est un nombre entier naturel.
2N + 1 est le successeur d'un nombre pair, il est donc impair.
L'affirmation 3 est vraie.
4. AB2 = 6,42 = 40,96
BC2 = 4,82 = 23,04
40,96 + 23,04 = 64
AC2 = 82 = 64
Donc AB2 + BC2 = AC2.
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
L'affirmation 4 est vraie.
BC2 = 4,82 = 23,04
40,96 + 23,04 = 64
AC2 = 82 = 64
Donc AB2 + BC2 = AC2.
D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B.
L'affirmation 4 est vraie.
Exercice 3
1. Nombre de carrés de la rosace
La rosace comporte 6 carrés.
La rosace comporte 6 carrés.
2. Transformation géométrique permettant de passer d'un carré au suivant
On passe d'un carré au suivant (du point de vue du programme) par la rotation de centre le point commun à tous les carrés et d'angle 60° dans le sens antihoraire.
On passe d'un carré au suivant (du point de vue du programme) par la rotation de centre le point commun à tous les carrés et d'angle 60° dans le sens antihoraire.
Remarque
Du point de vue de la figure seule, on peut aussi considérer la rotation d'angle 60° dans le sens horaire…3. Modifications à apporter au programme pour Clément
Pour que la rosace soit composée de 10 motifs, il faut remplacer « répéter 6 fois » par : « répéter 10 fois » et remplacer : « tourner de 60° » par « tourner de 36° », car 360° ÷ 10 = 36°.
Pour que la rosace soit composée de 10 motifs, il faut remplacer « répéter 6 fois » par : « répéter 10 fois » et remplacer : « tourner de 60° » par « tourner de 36° », car 360° ÷ 10 = 36°.
4. Modifications à apporter au programme pour Iness
Iness doit remplacer l'instruction « tourner de 60 degrés » par « avancer de 60 ».
Iness doit remplacer l'instruction « tourner de 60 degrés » par « avancer de 60 ».
Remarque
Attention, dans l'avancement, il faut prendre en compte les 10 unités de longueur qui séparent un carré du suivant, mais aussi la longueur du côté du carré, car le tracé du carré s'achève en bas à gauche.Exercice 4
1.
a) Probabilité pour que Mourad gagne
Mourad a un dé avec 5 faces rouges (R) et 1 face bleue (B) ; le dé de Kelly a 4 faces rouges et 2 bleues. On considère que l'obtention des différentes faces est équiprobable.
Mourad gagne si le tirage est : RR ou BB, la première lettre correspondant au dé de Mourad et la deuxième à celui de Kelly (nous adopterons cette convention d'écriture dans la suite).
Notons : P(M) la probabilité que Mourad gagne et P(K) celle que ce soit Kelly qui gagne.
On a : P(M) = P(RR) + P(BB) =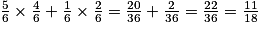 .
.
La probabilité que Mourad gagne est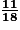 .
.
Mourad a un dé avec 5 faces rouges (R) et 1 face bleue (B) ; le dé de Kelly a 4 faces rouges et 2 bleues. On considère que l'obtention des différentes faces est équiprobable.
Mourad gagne si le tirage est : RR ou BB, la première lettre correspondant au dé de Mourad et la deuxième à celui de Kelly (nous adopterons cette convention d'écriture dans la suite).
Notons : P(M) la probabilité que Mourad gagne et P(K) celle que ce soit Kelly qui gagne.
On a : P(M) = P(RR) + P(BB) =
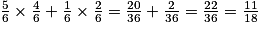 .
.La probabilité que Mourad gagne est
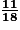 .
.Remarque
Vous pouvez aussi lister tous les couples de résultats (couleur du dé de Mourad ; couleur du dé de Kelly) en réalisant un tableau à double entrée ou en traçant un arbre de choix, puis dénombrer le nombre d'issues favorables, le nombre total d'issues et calculer le quotient des deux.b) Pertinence du coloriage pour répondre affirmativement à la question de Mourad et Kelly
Mourad et Kelly ont la même probabilité de gagner si cette probabilité est, pour chacun d'eux, de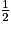 . Or :
. Or : 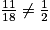 .
.
Le coloriage proposé ne permet donc pas de répondre affirmativement à la question que Mourad et Kelly se posent.
Mourad et Kelly ont la même probabilité de gagner si cette probabilité est, pour chacun d'eux, de
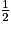 . Or :
. Or : 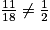 .
.Le coloriage proposé ne permet donc pas de répondre affirmativement à la question que Mourad et Kelly se posent.
2.
a) Probabilité pour que Mourad gagne
Soit x le nombre de faces coloriées en rouge sur le dé de Kelly. Il y a donc 6 − x faces coloriées en bleu sur son dé.
On a : P(M) = P(RR) + P(BB) =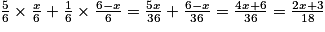 .
.
La probabilité que Morad gagne est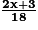 .
.
Soit x le nombre de faces coloriées en rouge sur le dé de Kelly. Il y a donc 6 − x faces coloriées en bleu sur son dé.
On a : P(M) = P(RR) + P(BB) =
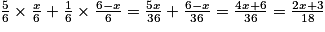 .
.La probabilité que Morad gagne est
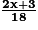 .
.b) Valeur de x pour répondre à la question de Mourad et Kelly
Remarque
La question est mal posée ; il faut comprendre : « valeur de x pour répondre affirmativement à la question que Kelly et Mourad se posent » (on peut cependant toujours répondre à la question).Pour que Mourad et Kelly aient les mêmes chances de gain, il faut que la probabilité de gain de Mourad soit de  , donc que :
, donc que : 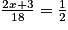 .
.
D'où : 2x + 3 = 9, soit 2x = 6 et x = 3.
Mourad et Kelly auront la même probabilité de gagner si le dé de Kelly comporte 3 faces rouges (et donc 3 faces bleues).
 , donc que :
, donc que : 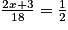 .
.D'où : 2x + 3 = 9, soit 2x = 6 et x = 3.
Mourad et Kelly auront la même probabilité de gagner si le dé de Kelly comporte 3 faces rouges (et donc 3 faces bleues).
Troisième partie
Situation 1
Remarque
Analyse succincte du problème (à faire sur le brouillon)Il y a deux façons de décomposer le problème en problèmes basiques sous-jacents :
- soit on considère qu'il s'agit de deux transformations d'état successives négatives, avec à chaque fois une recherche de l'état final : 1) il y a 100 places dans l'album photos, Rémi en occupe 24, combien en reste-t-il ? (rép. 100 − 24 = 76), puis 2) il y a 76 places dans l'album photos, Chloé en occupe 16, combien en reste-t-il ? (rép. 76 − 16 = 60) ;
- soit on considère un premier problème de composition d'état : 1) Rémi a 24 photos et Chloé en a 16, combien en ont-ils à eux deux ? (rép. 24 + 16 = 40), puis un deuxième problème de transformation négative : 2) il y a 100 places dans l'album photos, Rémi et Chloé en occupent 40, combien en reste-t-il ? (rép. 100 − 40 = 60).
Le champ numérique est inférieur à 100, afin de rester dans un domaine familier à des élèves de CE1.
1. Analyse des productions d'élèves au regard des compétences « modéliser » et « calculer »
• Du point de vue de la compétence « modéliser »
Les élèves A et E sont ceux qui ne réussissent pas à modéliser la situation par les bonnes opérations. L'élève A additionne les trois nombres de l'énoncé, sans probablement se représenter le problème. L'élève E soustrait 16 de 24, sans tenir compte de la première donnée 100. Il est probablement focalisé sur l'ostensif « reste-t-il » de la question, qui appelle une soustraction.
Les élèves B et D modélisent la situation par une succession de deux soustractions. 100 − 24, qui correspond au problème basique sous-jacent : « il y a 100 places dans l'album photos, Rémi en occupe 24, combien en reste-t-il ? », puis R − 16 (où R est le résultat de la première opération 100 − 24), qui correspond au problème basique sous-jacent : « il y a R places dans l'album photos, Chloé en occupe 16, combien en reste-t-il ? ».
L'élève C modélise le problème par une addition (24 + 16) correspondant au problème basique sous-jacent : « Rémi a 24 photos et Chloé en a 16 ; combien en ont-ils à eux deux ? », suivie d'une soustraction (100 − R, où R est le résultat de l'addition) correspondant au problème basique sous-jacent : « il y a 100 places dans l'album photos, Rémi et Chloé en occupent R, combien en reste-t-il ? ».
Les élèves A et E sont ceux qui ne réussissent pas à modéliser la situation par les bonnes opérations. L'élève A additionne les trois nombres de l'énoncé, sans probablement se représenter le problème. L'élève E soustrait 16 de 24, sans tenir compte de la première donnée 100. Il est probablement focalisé sur l'ostensif « reste-t-il » de la question, qui appelle une soustraction.
Les élèves B et D modélisent la situation par une succession de deux soustractions. 100 − 24, qui correspond au problème basique sous-jacent : « il y a 100 places dans l'album photos, Rémi en occupe 24, combien en reste-t-il ? », puis R − 16 (où R est le résultat de la première opération 100 − 24), qui correspond au problème basique sous-jacent : « il y a R places dans l'album photos, Chloé en occupe 16, combien en reste-t-il ? ».
L'élève C modélise le problème par une addition (24 + 16) correspondant au problème basique sous-jacent : « Rémi a 24 photos et Chloé en a 16 ; combien en ont-ils à eux deux ? », suivie d'une soustraction (100 − R, où R est le résultat de l'addition) correspondant au problème basique sous-jacent : « il y a 100 places dans l'album photos, Rémi et Chloé en occupent R, combien en reste-t-il ? ».
• Du point de vue de la compétence « calculer »
Les élèves A et B effectuent leurs calculs à l'aide d'un algorithme de pose, alors que les élèves C, D et E effectuent leurs calculs en ligne, et sont donc probablement davantage dans du calcul réfléchi.
L'addition posée de l'élève A est effectuée correctement, avec une gestion mentale de la retenue (pas de trace écrite).
L'élève B, ayant posé deux soustractions, enlève systématiquement le plus petit nombre du plus grand, quelle que soit sa place (en haut ou en bas). Ses deux calculs sont ainsi inexacts.
Les trois élèves ayant utilisé un calcul en ligne, C, D et E, effectuent les calculs mentalement et correctement, sans que l'on sache comme ils ont procédé. On peut noter que commencer par l'addition est techniquement plus facile.
Les élèves A et B effectuent leurs calculs à l'aide d'un algorithme de pose, alors que les élèves C, D et E effectuent leurs calculs en ligne, et sont donc probablement davantage dans du calcul réfléchi.
L'addition posée de l'élève A est effectuée correctement, avec une gestion mentale de la retenue (pas de trace écrite).
L'élève B, ayant posé deux soustractions, enlève systématiquement le plus petit nombre du plus grand, quelle que soit sa place (en haut ou en bas). Ses deux calculs sont ainsi inexacts.
Les trois élèves ayant utilisé un calcul en ligne, C, D et E, effectuent les calculs mentalement et correctement, sans que l'on sache comme ils ont procédé. On peut noter que commencer par l'addition est techniquement plus facile.
Remarque
On peut noter que la disposition des calculs de l'élève D est incorrecte d'un point de vue mathématique, mais cela ne relève pas des deux compétences analysées.2. Remédiation pour l'élève A
L'élève A a très probablement des difficultés à se représenter le problème. Pour l'accompagnement dans cette activité essentielle de représentation mentale, on peut l'encourager à vivre, réellement ou virtuellement, la situation :
L'élève A a très probablement des difficultés à se représenter le problème. Pour l'accompagnement dans cette activité essentielle de représentation mentale, on peut l'encourager à vivre, réellement ou virtuellement, la situation :
• Avec matériel : en respectant ou non le champ numérique (on peut notablement le baisser), on lui propose un album photos vide, dont il doit dénombrer les pages, puis une collection de photos, qu'il doit d'abord dénombrer, avant de devoir déterminer la quantité de places restantes dans son album, une fois qu'il y aura déposé toutes ses photos. Il doit anticiper cette quantité avant de pouvoir vérifier son hypothèse par une manipulation, afin de l'obliger à une opération mentale (dans l'idéal, une opération) pour résoudre le problème.
• Sans matériel : on peut lui proposer de dessiner la situation, de façon plus ou moins schématisée, afin d'accompagner la création de sa représentation mentale par une représentation physique (ici, un dessin). Toutes les données, mais aussi les relations entre ces données, ainsi que la question, doivent figurer sur son schéma. On peut par exemple lui imposer qu'un élève devra résoudre le problème à partir de son schéma seul.
3. Remédiation pour l'élève B
L'élève B ne connaît pas la technique de pose d'une soustraction.
Pour la construire efficacement et durablement, il faut en comprendre le mécanisme, en particulier le rôle des unités de numération.
On peut donc utiliser avec profit du matériel de numération, ici par exemple, partir de 8 barres de dizaines et 4 cubes unités dont on se propose d'enlever 16 cubes. La nécessité de « casser » une barre pour obtenir 10 cubes permet de matérialiser l'algorithme de soustraction.
On peut également inviter l'élève, préalablement, à vérifier son calcul (par exemple par une addition), lui permettant ainsi de se rendre compte de son erreur.
L'élève B ne connaît pas la technique de pose d'une soustraction.
Pour la construire efficacement et durablement, il faut en comprendre le mécanisme, en particulier le rôle des unités de numération.
On peut donc utiliser avec profit du matériel de numération, ici par exemple, partir de 8 barres de dizaines et 4 cubes unités dont on se propose d'enlever 16 cubes. La nécessité de « casser » une barre pour obtenir 10 cubes permet de matérialiser l'algorithme de soustraction.
On peut également inviter l'élève, préalablement, à vérifier son calcul (par exemple par une addition), lui permettant ainsi de se rendre compte de son erreur.
4. Deux difficultés ne pouvant être détectées par l'enseignant lorsqu'il propose le deuxième problème
Ce deuxième problème est un problème élémentaire, qui correspond à la première étape du problème initial. L'enseignant ne pourra donc pas détecter la difficulté que peuvent avoir certains élèves à percevoir les problèmes sous-jacents à un problème complexe.
De plus, la question comportant la locution « reste-t-il » appelle la soustraction, qui modélise effectivement ce problème. On ne pourra donc pas détecter des élèves qui se tromperaient d'opération.
Ainsi, il est fort probable que les élèves D et E, par exemple, produiraient des réponses correctes : l'élève D, parce qu'avec un seul calcul à produire, l'erreur d'écriture n'aurait pas lieu d'être commise ; l'élève E, parce que la connexion des seules données fournies, avec l'inducteur très intuitif « reste », lui serait largement facilitée.
Ce deuxième problème est un problème élémentaire, qui correspond à la première étape du problème initial. L'enseignant ne pourra donc pas détecter la difficulté que peuvent avoir certains élèves à percevoir les problèmes sous-jacents à un problème complexe.
De plus, la question comportant la locution « reste-t-il » appelle la soustraction, qui modélise effectivement ce problème. On ne pourra donc pas détecter des élèves qui se tromperaient d'opération.
Ainsi, il est fort probable que les élèves D et E, par exemple, produiraient des réponses correctes : l'élève D, parce qu'avec un seul calcul à produire, l'erreur d'écriture n'aurait pas lieu d'être commise ; l'élève E, parce que la connexion des seules données fournies, avec l'inducteur très intuitif « reste », lui serait largement facilitée.
Situation 2
1. Notions en jeu dans l'exercice
Il fallait citer deux notions, au choix parmi les suivantes :
Domaine « Grandeur et mesures »
Il fallait citer deux notions, au choix parmi les suivantes :
Domaine « Grandeur et mesures »
- le lien entre l'aire d'un rectangle et les longueurs de ses côtés (autrement dit, la formule de l'aire) ;
- la distinction entre l'aire et le périmètre d'une surface (connaître au préalable ces deux notions) ;
- les unités de mesure d'aires et de longueur, et leur lien.
- la résolution d'une multiplication à trous (multiplication et division) ;
- la décomposition multiplicative d'un nombre.
- la définition d'un rectangle (un peu trop évident).
2. Réponses possibles au problème
| Couple | (1 ; 16) | (2 ; 8) | (4 ; 4) | (5 ; 3,2) |
|---|---|---|---|---|
| Aire (non demandé) | 1 × 16 cm2 | 2 × 8 cm2 | 4 × 4 cm2 | 5 × 3,2 cm2 |
3. Difficultés rencontrées par les élèves
La première est de décomposer multiplicativement un nombre, soit résoudre une équation du type 16 = … × … ; il s'agit d'utiliser ses compétences de la multiplication à l'envers.
La seconde est de trouver des solutions non entières.
La première est de décomposer multiplicativement un nombre, soit résoudre une équation du type 16 = … × … ; il s'agit d'utiliser ses compétences de la multiplication à l'envers.
La seconde est de trouver des solutions non entières.
4. Un carré est-il un rectangle ?
L'enseignant peut souligner la différence entre le langage courant et le langage mathématique :
L'enseignant peut souligner la différence entre le langage courant et le langage mathématique :
- dans la vie courante, un carré est une forme particulière différente du rectangle, le rectangle ayant nécessairement une longueur et une largeur différentes ;
- en mathématique, on peut rappeler la définition d'un rectangle, soit un quadrilatère ayant 4 angles droits, comme son nom l'indique, et faire ainsi apparaître le carré comme un cas particulier du rectangle : tout ce qui est vrai du rectangle l'est aussi pour le carré.
5. Le couple (3 cm ; 5,33 cm)
a) Hypothèse sur le raisonnement de l'élève
L'élève a fixé une longueur de 3 cm et a cherché quelle largeur permet d'obtenir une aire de 16 cm2.
Autrement dit, il a cherché à résoudre l'équation 3 × ? = 16.
La réponse est bien le résultat de la division de 16 par 3, le raisonnement de l'élève est correct.
L'élève a fixé une longueur de 3 cm et a cherché quelle largeur permet d'obtenir une aire de 16 cm2.
Autrement dit, il a cherché à résoudre l'équation 3 × ? = 16.
La réponse est bien le résultat de la division de 16 par 3, le raisonnement de l'élève est correct.
b) Acquis de l'élève
Cet élève utilise correctement la formule de l'aire, et le lien entre la multiplication et la division.
Il connaît également la technique algorithmique de la potence pour effectuer une division.
Il applique correctement cette technique avec les nombres décimaux non entiers, avec un usage correct de la virgule.
Cet élève utilise correctement la formule de l'aire, et le lien entre la multiplication et la division.
Il connaît également la technique algorithmique de la potence pour effectuer une division.
Il applique correctement cette technique avec les nombres décimaux non entiers, avec un usage correct de la virgule.
c) Montrer à l'élève que sa réponse ne convient pas
Remarque
Dire que cette réponse ne convient pas est très exagéré, et probablement contre-productif ; le raisonnement est parfaitement correct, la technique utilisée également.Le résultat est précis au centième de centimètre, autrement dit invisible à l'œil nu.
Dans le paradigme géométrique de la géométrie « dessinée », sa réponse est tout à fait valable.
On peut montrer à l'élève, en lui faisant effectuer le calcul 3 × 5,33 = 15,99, que l'aire du rectangle n'est pas exactement 16 cm2.
En revanche, cette aire est tellement proche de l'aire demandée que l'on ne peut faire la différence avec les instruments de construction.
En revanche, cette aire est tellement proche de l'aire demandée que l'on ne peut faire la différence avec les instruments de construction.
d) Utilisation en classe de la proposition de l'élève
Cette proposition est l'occasion de montrer que toutes les divisions ne peuvent pas nécessairement épuiser le reste, et la prise de conscience qu'il existe des nombres non décimaux.
Mais on est à la limite du programme de l'école.
Cette proposition est l'occasion de montrer que toutes les divisions ne peuvent pas nécessairement épuiser le reste, et la prise de conscience qu'il existe des nombres non décimaux.
Mais on est à la limite du programme de l'école.
Situation 3
1. Notion en jeu
La notion en jeu dans cette situation est la proportionnalité.
La notion en jeu dans cette situation est la proportionnalité.
2. Choix des nombres de crêpes
15 et 25 sont des nombres peu faciles à utiliser comme diviseurs, ce qui peut faire obstacle à une procédure du type « passage par l'unité ».
Leur différence (10) permet de répondre à la première question par une procédure purement additive. Cette réponse étant trouvée, on peut à nouveau répondre à la seconde question par une procédure strictement additive.
Par ailleurs, le nombre de crêpes demandé a systématiquement un diviseur commun avec les autres données du problème, ce qui favorise l'utilisation de la linéarité multiplicative ou des rapports constants.
15 et 25 sont des nombres peu faciles à utiliser comme diviseurs, ce qui peut faire obstacle à une procédure du type « passage par l'unité ».
Leur différence (10) permet de répondre à la première question par une procédure purement additive. Cette réponse étant trouvée, on peut à nouveau répondre à la seconde question par une procédure strictement additive.
Par ailleurs, le nombre de crêpes demandé a systématiquement un diviseur commun avec les autres données du problème, ce qui favorise l'utilisation de la linéarité multiplicative ou des rapports constants.
3. Trois procédures pour calculer la masse de farine pour 10 crêpes
• Procédure additive, appuyée sur la linéarité additive
15 crêpes utilisent 300 g de farine et 25 crêpes utilisent 500 g de farine.
Donc 10 crêpes (= 25 crêpes − 15 crêpes) utilisent 500 g − 300 g = 200 g de farine.
15 crêpes utilisent 300 g de farine et 25 crêpes utilisent 500 g de farine.
Donc 10 crêpes (= 25 crêpes − 15 crêpes) utilisent 500 g − 300 g = 200 g de farine.
• Procédure scalaire, appuyée sur la linéarité multiplicative (méthode 1)
15 crêpes utilisent 300 g de farine.
Donc 5 crêpes en utilisent 3 fois moins, soit 100 g de farine.
Et 10 crêpes en utilisent 2 fois plus (que 100 g), soit 200 g de farine.
15 crêpes utilisent 300 g de farine.
Donc 5 crêpes en utilisent 3 fois moins, soit 100 g de farine.
Et 10 crêpes en utilisent 2 fois plus (que 100 g), soit 200 g de farine.
• Procédure scalaire, appuyée sur la linéarité multiplicative (méthode 2)
25 crêpes utilisent 500 g de farine.
Donc 100 crêpes en utilisent 4 fois plus, soit 2 000 g de farine.
Et 10 crêpes en utilisent 10 fois moins, soit 200 g de farine.
25 crêpes utilisent 500 g de farine.
Donc 100 crêpes en utilisent 4 fois plus, soit 2 000 g de farine.
Et 10 crêpes en utilisent 10 fois moins, soit 200 g de farine.
• Procédure appuyée sur les rapports constants
25 crêpes utilisent 500 g de farine.
Or, 500 = 5 × 100 = 5 × 4 × 25 = 20 × 25.
Donc, pour obtenir la masse de farine, il suffit de multiplier le nombre de crêpes par 20.
Donc, pour 10 crêpes, il faut 20 × 10 = 200 g de farine.
25 crêpes utilisent 500 g de farine.
Or, 500 = 5 × 100 = 5 × 4 × 25 = 20 × 25.
Donc, pour obtenir la masse de farine, il suffit de multiplier le nombre de crêpes par 20.
Donc, pour 10 crêpes, il faut 20 × 10 = 200 g de farine.
4. Analyse de la production d'un élève
• Question 1 : pour 10 crêpes
Cet élève utilise la première procédure décrite pour calculer les ingrédients.
Toutes ses opérations sont correctes, mais il fait une erreur de calcul pour effectuer 125 − 75.
Il est probable qu'il a utilisé une technique algorithmique, en soustrayant unité de numération par unité de numération, et donc, pour les dizaines, a fait 7 − 2.
On peut lui proposer une technique de calcul réfléchi plutôt qu'algorithmique, et commencer par lui faire prendre conscience que son résultat, plus grand que les deux nombres de départ, ne peut être possible.
Cet élève utilise la première procédure décrite pour calculer les ingrédients.
Toutes ses opérations sont correctes, mais il fait une erreur de calcul pour effectuer 125 − 75.
Il est probable qu'il a utilisé une technique algorithmique, en soustrayant unité de numération par unité de numération, et donc, pour les dizaines, a fait 7 − 2.
On peut lui proposer une technique de calcul réfléchi plutôt qu'algorithmique, et commencer par lui faire prendre conscience que son résultat, plus grand que les deux nombres de départ, ne peut être possible.
• Question 2 : pour 60 crêpes
Il utilise une procédure mixte, basée sur les deux propriétés de linéarité :
60 = 15 + 25 + 2 × 10.
Toutes ses opérations sont correctes, si l'on ne tient pas compte de la valeur 300, double de 150, valeur erronée établie à la question précédente.
Ses résultats également.
Il utilise une procédure mixte, basée sur les deux propriétés de linéarité :
60 = 15 + 25 + 2 × 10.
Toutes ses opérations sont correctes, si l'on ne tient pas compte de la valeur 300, double de 150, valeur erronée établie à la question précédente.
Ses résultats également.
Document précédent
Sujet 2020, groupement académique 1
Document suivant
Sujet 2020, groupement académique 3
