Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
Dans cette partie, les figures qui sont représentées dans l'énoncé ne sont pas dessinées à l'échelle.
A. Situation des trois carrés
La figure ci-dessous représente trois carrés dont les mesures des côtés, en centimètres, sont respectivement 3 cm, 4 cm et 5 cm. Les deux plus petits carrés sont gris, le troisième est blanc.
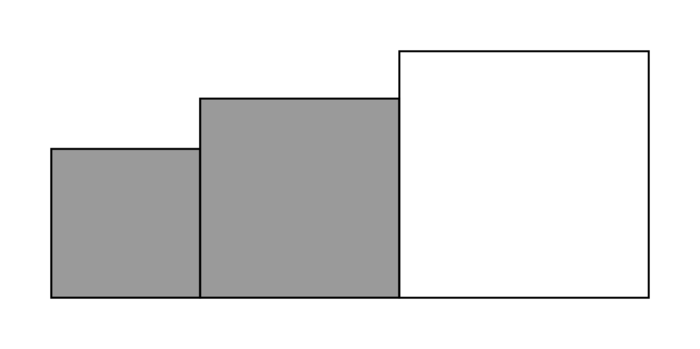 |
1. Vérifier que la somme des aires des deux carrés gris est égale à l'aire du carré blanc.
2. Claude affirme : « Si on dispose les trois carrés obtenus à la question précédente comme sur la figure 1 ci-dessous, alors le triangle ABC est un triangle rectangle. »
L'affirmation de Claude est-elle vraie ou fausse ? Justifier la réponse.
L'affirmation de Claude est-elle vraie ou fausse ? Justifier la réponse.
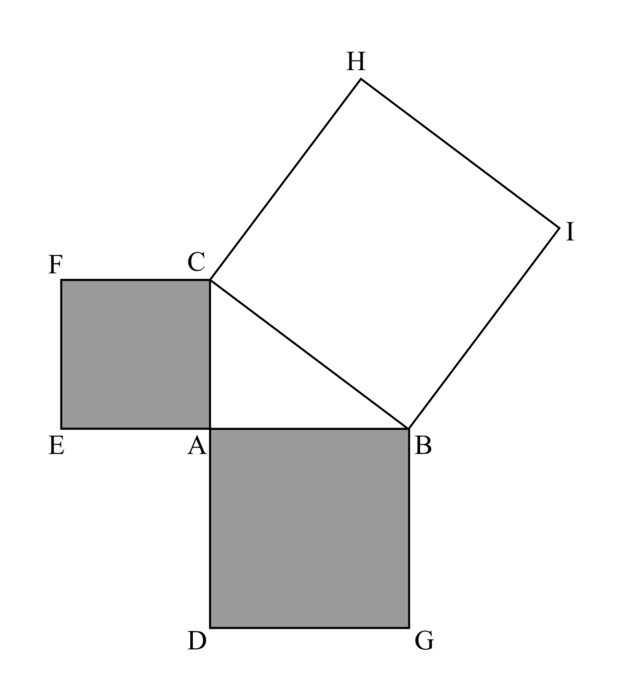 |
3. Avec les mêmes carrés, Dominique affirme : « Sur la figure 2 ci-dessous, les longueurs exactes, en centimètres, des segments [MN] et [IJ] sont des nombres décimaux. » L'affirmation de Dominique est-elle vraie ou fausse ? Justifier la réponse.
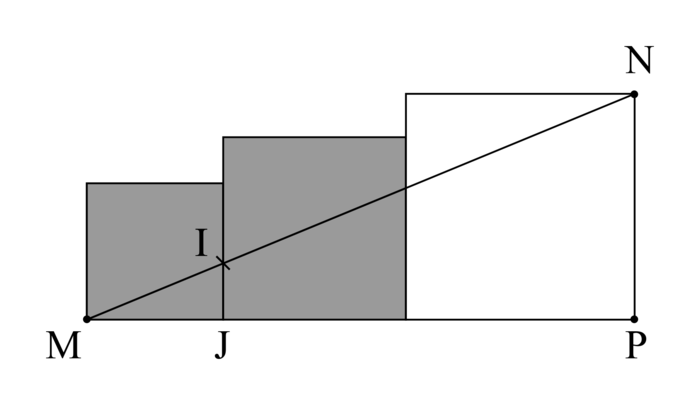 |
4. Avec les mêmes carrés, Camille affirme : « Sur la figure 3 ci-dessous, les points R, S et T sont alignés. »
L'affirmation de Camille est-elle vraie ou fausse ? Justifier la réponse.
L'affirmation de Camille est-elle vraie ou fausse ? Justifier la réponse.
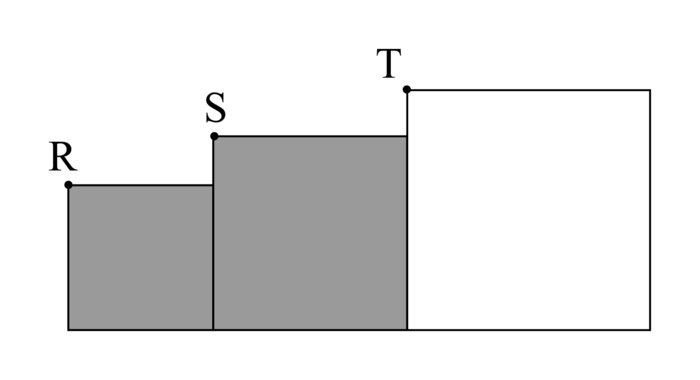 |
B. Situation des cinq carrés
La figure ci-dessous, qui n'est pas à l'échelle, représente cinq carrés dont les mesures des côtés, en centimètres, sont des nombres entiers consécutifs. Les trois plus petits carrés sont gris, les deux autres sont blancs.
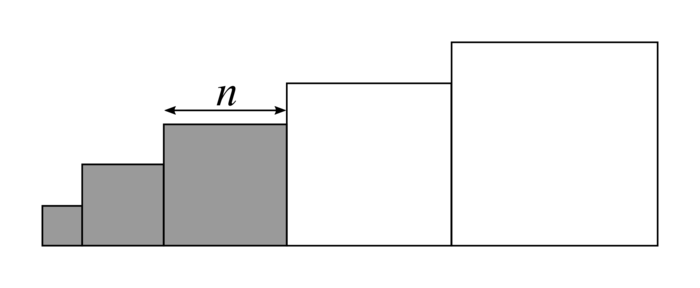 |
On désigne par n la mesure, exprimée en centimètres, du côté du carré gris le plus grand (carré du milieu). L'objectif de cette partie est de chercher les valeurs de n pour lesquelles la somme des aires des trois carrés gris est égale à la somme des aires des deux carrés blancs.
1. Montrer que résoudre ce problème revient à résoudre l'équation n2 − 12n = 0.
2. Quelles sont les solutions de l'équation n2 − 12n = 0 ? Justifier la réponse.
3. Ces solutions peuvent-elles être retenues pour le problème de la « situation des cinq carrés » ? Justifier votre réponse.
4. Réaliser une figure à l'échelle 1/5 d'une solution du problème de la « situation des cinq carrés » en détaillant les calculs effectués pour construire la figure.
C. Situation des sept carrés
On s'intéresse maintenant à une figure comportant sept carrés. Les mesures, en centimètres, des côtés des sept carrés sont des entiers consécutifs. Les quatre plus petits carrés sont gris et les trois autres sont blancs.
On cherche s'il est possible de trouver des longueurs pour les côtés des carrés telles que la somme des aires des quatre carrés gris soit égale à celle des trois carrés blancs.
On cherche s'il est possible de trouver des longueurs pour les côtés des carrés telles que la somme des aires des quatre carrés gris soit égale à celle des trois carrés blancs.
On envisage une résolution graphique. On choisit comme variable x la longueur (en cm) du côté du plus grand carré blanc. On admet que l'expression algébrique de la somme des aires des carrés gris est alors :
4x2 − 36x + 86
et que l'expression algébrique de la somme des aires des carrés blancs est :
3x2 − 6x + 5.
4x2 − 36x + 86
et que l'expression algébrique de la somme des aires des carrés blancs est :
3x2 − 6x + 5.
On nomme :
- f la fonction qui à tout nombre x fait correspondre f(x) = 4x2 − 36x + 86 ;
- g la fonction qui à tout nombre x fait correspondre g(x) = 3x2 − 6x + 5.
La copie d'écran ci-dessous fait apparaître une partie des représentations graphiques de ces deux fonctions, obtenues à l'aide d'un logiciel.
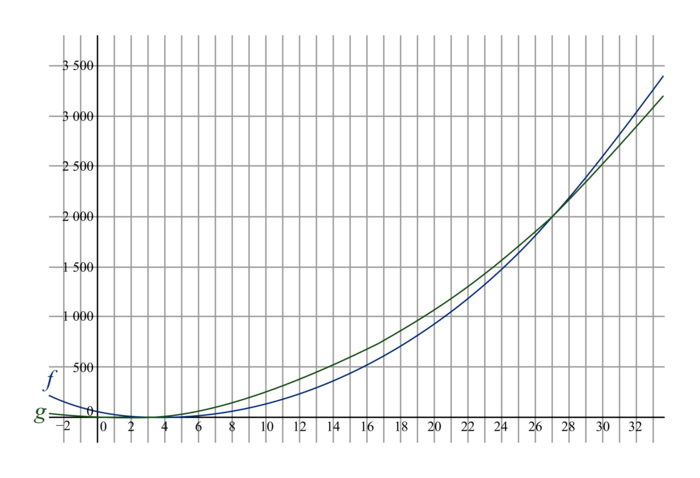 |
1. Déterminer graphiquement si la situation des sept carrés semble avoir des solutions.
2. Vérifier si la ou les solutions trouvées conviennent.
D. Situation des quatre carrés
Avec quatre carrés ayant des côtés de mesures entières et consécutives, on peut envisager au moins deux cas :
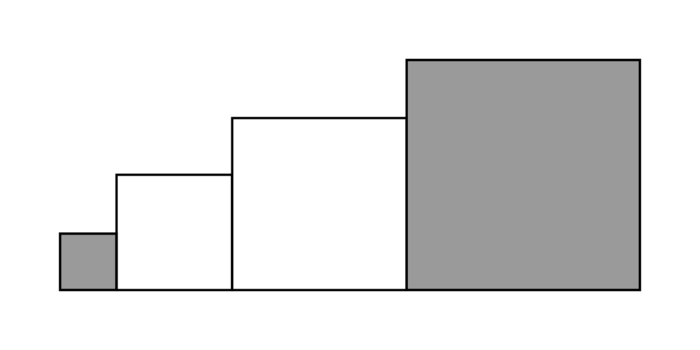 |
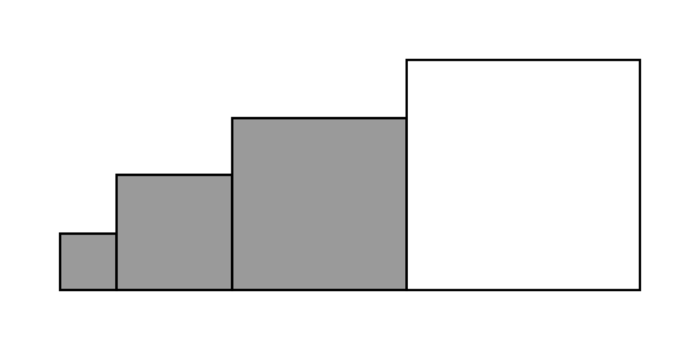 |
On cherche à savoir si, dans chacun de ces cas, il est possible que l'aire de la surface grise soit égale à l'aire de la surface blanche.
On utilise pour cela un tableur. On donne ci-dessous les copies d'écran des feuilles de calcul obtenues lors de cette recherche.
On utilise pour cela un tableur. On donne ci-dessous les copies d'écran des feuilles de calcul obtenues lors de cette recherche.
Copies d'écran :
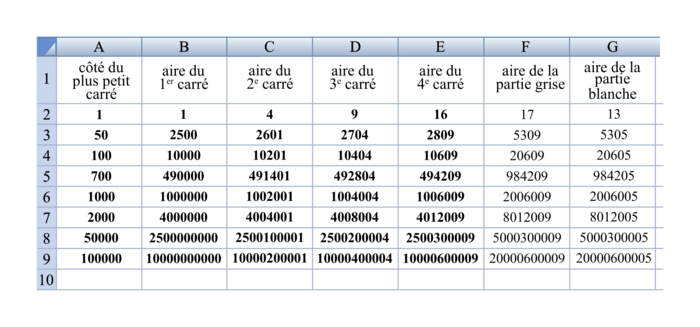 |
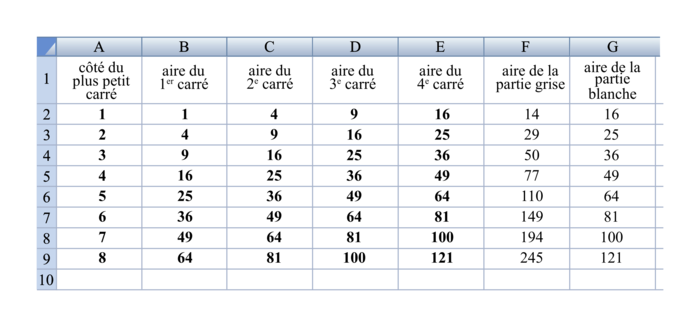 |
1. Quelle feuille correspond à chacun des deux cas ? Justifier la réponse.
2. Pour la feuille de calcul A :
a) Quelle formule étirable vers le bas a-t-on pu saisir dans la cellule E2 pour calculer l'aire du quatrième carré à partir de la valeur saisie dans la cellule A2 ?
b) Quelle formule étirable vers le bas a-t-on pu saisir dans la cellule F2 pour calculer l'aire de la partie grise ?
3. Pour chaque cas, quelle conjecture sur les solutions du problème la copie d'écran de la feuille de calcul permet-elle d'émettre ? Justifier la réponse.
4. Démontrer que, dans les deux cas, la « situation des quatre carrés » n'admet pas de solution.
Deuxième partie (13 points)
Cette partie est composée de trois exercices indépendants.
Exercice 1
Indiquer si les affirmations suivantes sont vraies ou fausses en justifiant la réponse. Une réponse exacte mais non justifiée ne rapporte aucun point. Une réponse fausse n'enlève pas de points.
1. Les tableaux ci-dessous résument les productions par deux sociétés de deux types de tablettes : la tablette Electrix et la tablette Tronix.
| Nombre de tablettes fabriquées par jour | Pourcentage moyen de tablettes défectueuses | |
|---|---|---|
| Electrix | 2 000 | 5 % |
| Tronix | 7 000 | 2 % |
Société 1
| Nombre de tablettes fabriquées par jour | Pourcentage moyen de tablettes défectueuses | |
|---|---|---|
| Electrix | 6 000 | 3 % |
| Tronix | 1 000 | 2 % |
Société 2
Affirmation : Pour l'ensemble des tablettes produites, la société 1 a le pourcentage d'appareils défectueux le plus faible.
2. On sait que l'aire d'un cube est égale à la somme des aires des faces qui le constituent.
Affirmation : Le volume d'un cube est proportionnel à son aire.
Affirmation : Le volume d'un cube est proportionnel à son aire.
3. Un récupérateur d'eau de pluie contient 0,3 m3 d'eau.
Pour arroser un potager il faut 15 L d'eau par m2.
Affirmation : Avec l'eau du récupérateur, on peut arroser quatre fois un potager de 5 m2.
Pour arroser un potager il faut 15 L d'eau par m2.
Affirmation : Avec l'eau du récupérateur, on peut arroser quatre fois un potager de 5 m2.
4. A = 7 + 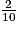
Affirmation : La partie décimale de A2 est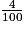 .
.
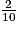
Affirmation : La partie décimale de A2 est
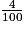 .
.Exercice 2
1. Inès a lancé 200 fois un dé équilibré à 6 faces et a collecté ses résultats dans un tableau.
| Nombre affiché sur la face | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Nombre d'apparitions | 30 | 41 | 32 | 28 | 31 |
a) Combien de fois a-t-elle obtenu 6 ?
b) Quelle est, en pourcentage, la fréquence d'apparition du « 1 » ?
2. Inès lance cette fois deux dés équilibrés à 6 faces.
a) Quelle est la probabilité d'obtenir deux nombres dont le produit est égal à 9 ?
b) Quelle est la probabilité d'obtenir deux nombres dont le produit est égal à 12 ?
Exercice 3
Un polygone régulier est un polygone convexe dont tous les côtés ont la même longueur et tous les angles ont la même mesure.
| Au cours de cet exercice, on pourra utiliser le résultat admis suivant : « La somme des mesures en degré des angles d'un polygone régulier à n côtés vaut 180n − 360. » |
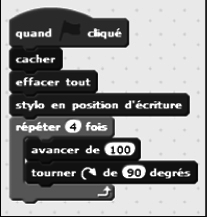
1. Déterminer, sans justifier, la nature des deux figures tracées lorsqu'on exécute le programme A et le programme B.
 |
 |
2. On considère le pentagone régulier ABCDE ci-dessous. F est un point de la droite (AB) n'appartenant pas à la demi-droite [BA).
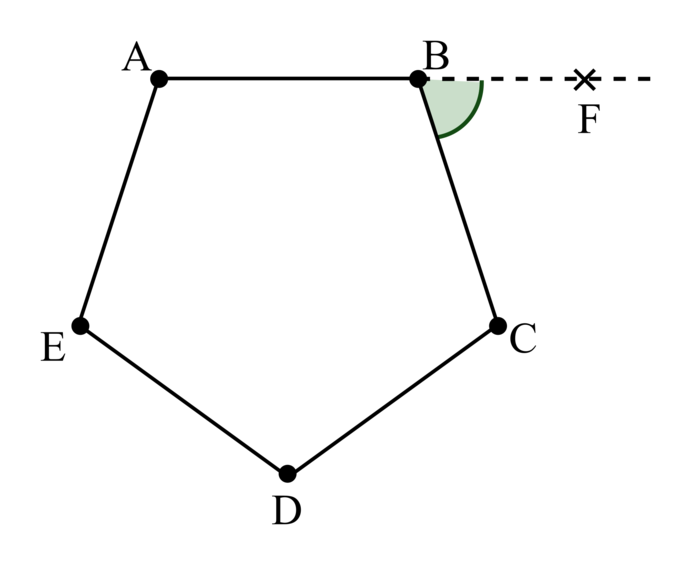 |
a) Démontrer que 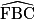 = 72°.
= 72°.
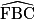 = 72°.
= 72°.b) En déduire les modifications à apporter au programme A pour que la figure tracée soit un pentagone régulier.
Pour la suite de l'exercice, on admet que, pour tout polygone régulier, l'angle 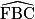 est égal à 360 divisé par le nombre de côtés de ce polygone.
est égal à 360 divisé par le nombre de côtés de ce polygone.
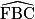 est égal à 360 divisé par le nombre de côtés de ce polygone.
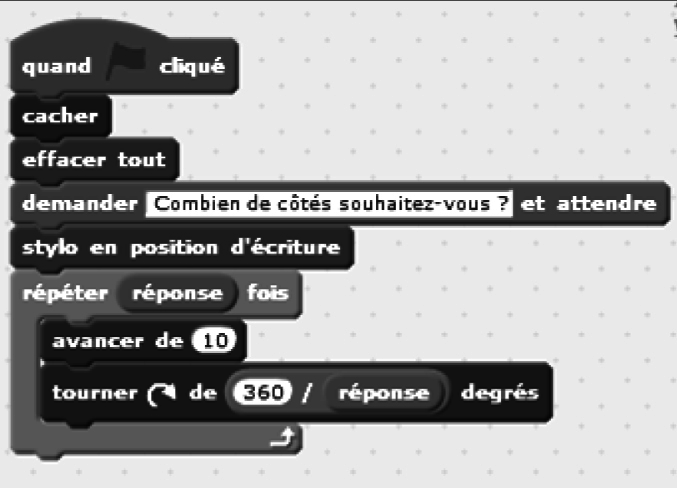
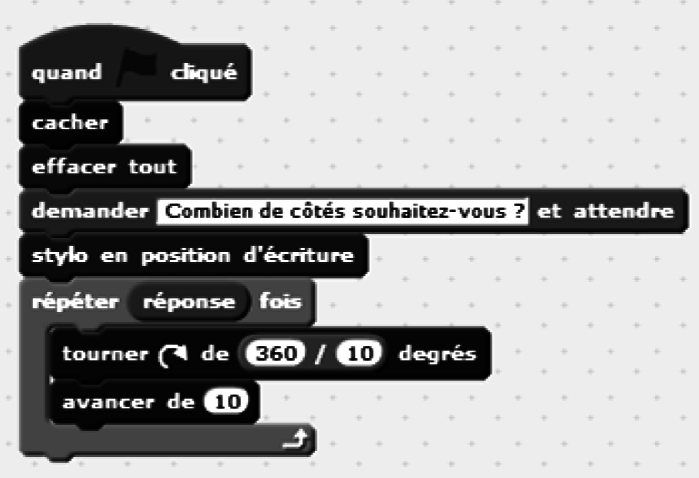
est égal à 360 divisé par le nombre de côtés de ce polygone.3. On souhaite maintenant réaliser un programme qui, lorsqu'on l'exécute, permet d'obtenir le tracé d'un polygone régulier dont le nombre de côtés est choisi par l'utilisateur. Voici les programmes élaborés par quatre élèves.
Lequel de ces quatre programmes permet de réaliser le tracé souhaité ? Préciser pourquoi les autres ne conviennent pas.
Lequel de ces quatre programmes permet de réaliser le tracé souhaité ? Préciser pourquoi les autres ne conviennent pas.
 |
 |
 |
 |
Rappel
Une fois que l'utilisateur a répondu à la question « Combien de côtés souhaitez-vous ? », la valeur indiquée est stockée dans la variable « réponse ».
Une fois que l'utilisateur a répondu à la question « Combien de côtés souhaitez-vous ? », la valeur indiquée est stockée dans la variable « réponse ».
4. Le programme Scratch ne permet pas de tracer facilement un cercle. Comment peut-on utiliser le travail mené dans cet exercice pour construire, avec Scratch, une figure ayant l'apparence d'un cercle à l'écran ?
Troisième partie (14 points)
Situation 1
Dans une classe de maternelle, une enseignante donne à un groupe d'élèves la consigne suivante :
| « Vous devez aller chercher des voyageurs pour remplir le petit train, pas un de plus, pas un de moins. Vous poserez les voyageurs sur le quai. » |
Matériel :
- des jetons représentant les voyageurs (ils sont placés dans une boîte éloignée dans un coin de la classe) ;
- un support pour chaque élève représentant des places libres ou occupées ;
- une partie libre (le quai) sur lequel seront posés les voyageurs rapportés avant validation.
Le premier support proposé compte 7 places vides (blanches) et 3 places occupées (noires). Les places vides peuvent être organisées de différentes façons. Les élèves devront déposer les voyageurs sur le quai (zone grisée) avant de les faire monter à bord.
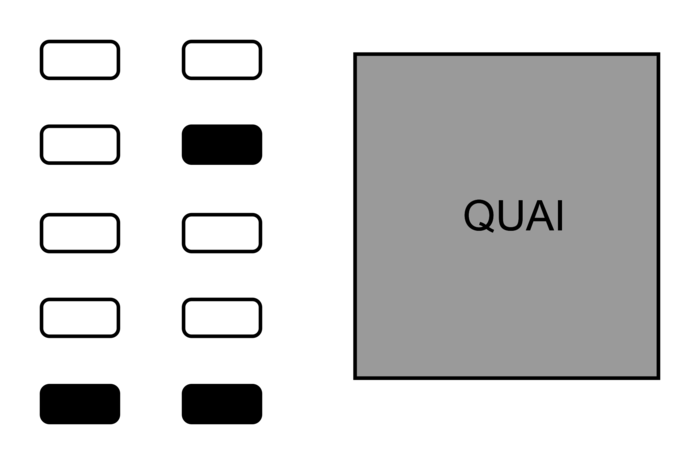 |
L'élève A a effectué deux voyages. Au premier voyage, il ramène une dizaine de jetons et au second il rapporte les jetons en trop.
L'élève B a effectué un voyage, il revient très rapidement avec 7 jetons.
L'élève C a effectué sept voyages, rapportant un seul jeton à la fois.
L'élève D a effectué un voyage. Il revient avec 4 jetons dans une main et 3 jetons dans l'autre main.
L'élève B a effectué un voyage, il revient très rapidement avec 7 jetons.
L'élève C a effectué sept voyages, rapportant un seul jeton à la fois.
L'élève D a effectué un voyage. Il revient avec 4 jetons dans une main et 3 jetons dans l'autre main.
1. Quel usage du nombre est mobilisé dans cette situation ?
2. Quel est l'intérêt du quai ?
3. Au regard des acquis liés à la notion du nombre, analyser les procédures mises en œuvre par chacun des élèves.
4. Proposer deux modifications de la tâche que l'enseignante peut proposer pour amener les élèves A ou C à progresser dans leur utilisation du nombre.
Situation 2
Un enseignant propose deux calculs à effectuer en ligne à des élèves de cycle 3 et relève quatre productions.
| Calcul 1 L'enseignant écrit au tableau : 12,42 − 6,8. et dit aux élèves : « Calculer la différence entre 12 unités et 42 centièmes, et 6 unités et 8 dixièmes. » | |
| Élève 1 12,42 − 6,8 = 6,42 − 0,8 = 6 − 0,38 = 5,62 | Élève 2 12 unités et 42 centièmes moins 6 unités et 8 dixièmes = 1 242 centièmes moins 68 dixièmes = 1 242 centièmes moins 680 centièmes 1 242 − 680 = 1 262 − 700 = 562 Résultat : 562 centièmes. |
| Calcul 2 Calculer le produit de 15 par 0,24. | |
| Élève 3 15 × 0,24 = 2,4 + 1,2 = 3,6 | Élève 4 15 × 24 centièmes = 300 centièmes + 60 centièmes = 360 centièmes |
1. Pour chaque calcul, analyser les productions des élèves au regard des connaissances mobilisées sur les nombres et sur les propriétés des opérations.
2. Pour chaque calcul, préciser ce qui distingue les productions des deux élèves.
Situation 3
Un professeur d'une classe de cycle 3 propose les trois exercices suivants, dans cet ordre, à ses élèves.
| Exercice 1 Un livre de cuisine indique que, pour faire de la crème brûlée, il faut 6 œufs si la recette est prévue pour 9 personnes et 10 œufs si la recette est prévue pour 15 personnes. Combien dois-je prévoir d'œufs si je veux faire cette crème brûlée pour 24 personnes ? J'ai chez moi tous les ingrédients dont j'ai besoin. |
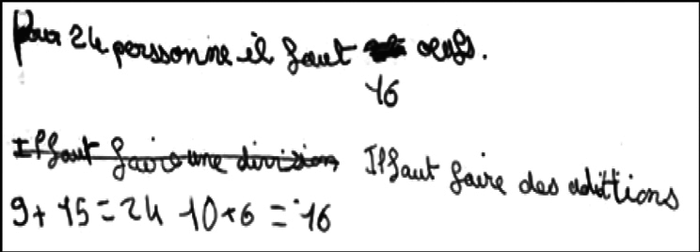 |
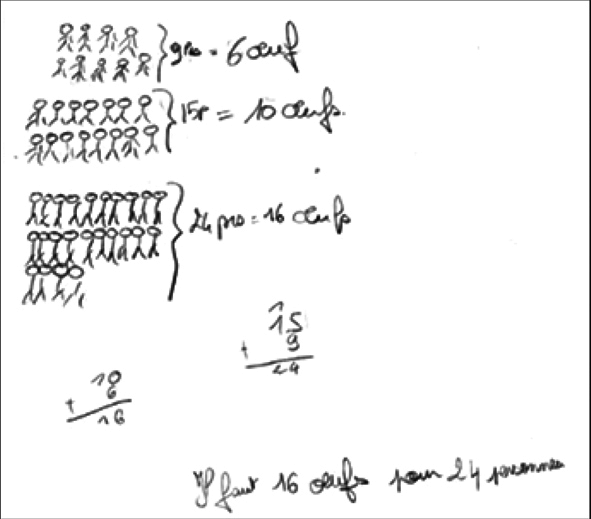 |
| Exercice 2 Il faut 6 œufs pour faire une crème au caramel pour 10 personnes. Combien dois-je prévoir d'œufs si je veux faire cette crème au caramel pour 15 personnes ? J'ai chez moi tous les ingrédients dont j'ai besoin. |
 |
| Exercice 3 Il faut 5 œufs pour faire une mousse au chocolat pour 10 personnes. J'ai 3 œufs. Pour combien de personnes puis-je faire une mousse au chocolat ? J'ai chez moi tout le chocolat dont j'ai besoin. |
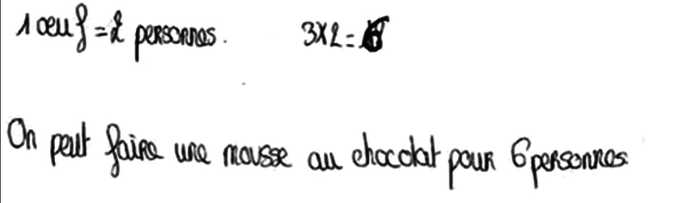 |
1. Quelle est la notion du programme que ces exercices permettent principalement de travailler ?
2. Analyser les productions des élèves A, B, C et D en indiquant le type de procédures utilisées.
3. Montrer en quoi les différences entre les trois énoncés permettent une progressivité dans l'apprentissage de la notion.
4. Proposer un exercice qui permettrait, en deuxième moitié de cycle 3, de poursuivre l'apprentissage de la notion travaillée.
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Situation des trois carrés
1. Somme des aires des deux carrés gris
La somme des aires des deux carrés gris est : 32 + 42 = 9 + 16 = 25.
L'aire du carré blanc est : 52 = 25.
La somme des aires des deux carrés gris est donc bien égale à l'aire du carré blanc.
La somme des aires des deux carrés gris est : 32 + 42 = 9 + 16 = 25.
L'aire du carré blanc est : 52 = 25.
La somme des aires des deux carrés gris est donc bien égale à l'aire du carré blanc.
2. Nature du triangle ABC
Nous venons de montrer à la question précédente que : AC2 + AB2 = BC2. D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en A.
L'affirmation de Claude est vraie.
Nous venons de montrer à la question précédente que : AC2 + AB2 = BC2. D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en A.
L'affirmation de Claude est vraie.
3. Nature des mesures des longueurs MN et IJ
Calculons les mesures, en centimètres, des longueurs MN et IJ.
Plaçons-nous dans le triangle MPN, rectangle en P. D'après le théorème de Pythagore, on a :
MP2 + PN2 = MN2. Or, NP = 5 et MP = 3 + 4 + 5 = 12, d'où MN2 = 52 + 122 = 25 + 144 = 169.
On en déduit : MN =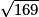 = 13.
= 13.
Considérons à présent les triangles MIJ et MNP : ils sont en configuration de Thalès. En effet, (MN) et (JP) sont sécantes en M, et (IJ) et (NP) sont parallèles. La démonstration du parallélisme de (IJ) et (NP) n'était pas attendue ici.
D'après le théorème de Thalès, on a donc :
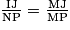 . D'où :
. D'où : 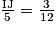 et donc : IJ =
et donc : IJ = 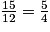 = 1,25.
= 1,25.
Les mesures en centimètres de IJ et MN (resp. 1,25 et 13) sont donc décimales car elles ont une écriture décimale finie.
L'affirmation de Dominique est vraie.
Calculons les mesures, en centimètres, des longueurs MN et IJ.
Plaçons-nous dans le triangle MPN, rectangle en P. D'après le théorème de Pythagore, on a :
MP2 + PN2 = MN2. Or, NP = 5 et MP = 3 + 4 + 5 = 12, d'où MN2 = 52 + 122 = 25 + 144 = 169.
On en déduit : MN =
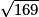 = 13.
= 13.Considérons à présent les triangles MIJ et MNP : ils sont en configuration de Thalès. En effet, (MN) et (JP) sont sécantes en M, et (IJ) et (NP) sont parallèles. La démonstration du parallélisme de (IJ) et (NP) n'était pas attendue ici.
D'après le théorème de Thalès, on a donc :
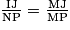 . D'où :
. D'où : 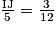 et donc : IJ =
et donc : IJ = 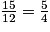 = 1,25.
= 1,25.Les mesures en centimètres de IJ et MN (resp. 1,25 et 13) sont donc décimales car elles ont une écriture décimale finie.
L'affirmation de Dominique est vraie.
Remarque
Attention ici à ne pas mobiliser une conception erronée qui serait : « un nombre décimal est un nombre à virgule » et qui conduirait à considérer – à tort – que 13 n'est pas un nombre décimal. Cette conception, selon laquelle les nombres entiers ne seraient pas des nombres décimaux est, hélas, assez répandue…4. Alignement des points R, S et T
Remarque
Plusieurs méthodes sont possibles, nous en donnons trois.Nommons deux points supplémentaires sur la figure, comme illustré ci-dessous :
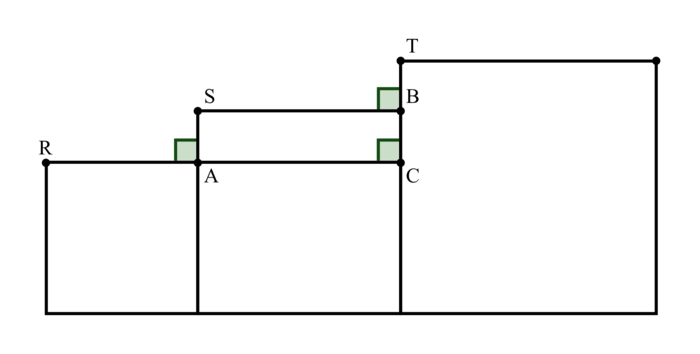 |
• 1re méthode : utilisation de la trigonométrie
Comme les triangles RAS et SBT sont rectangles et que les côtés [RA] et [SB] d'une part, [AS] et [BT] d'autre part, sont parallèles, les points RST sont alignés si et seulement si les angles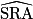 et
et 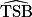 sont égaux.
sont égaux.
Dans le triangle RSA, rectangle en A, on a : tan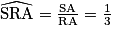 .
.
Dans le triangle TSB, rectangle en B, on a : tan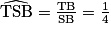 .
.
Les tangentes ne sont pas égales, donc les angles ne sont pas égaux.
Comme les triangles RAS et SBT sont rectangles et que les côtés [RA] et [SB] d'une part, [AS] et [BT] d'autre part, sont parallèles, les points RST sont alignés si et seulement si les angles
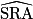 et
et 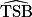 sont égaux.
sont égaux.Dans le triangle RSA, rectangle en A, on a : tan
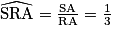 .
.Dans le triangle TSB, rectangle en B, on a : tan
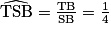 .
.Les tangentes ne sont pas égales, donc les angles ne sont pas égaux.
• 2e méthode : utilisation du théorème de Pythagore
Les points R, S et T sont alignés dans cet ordre si et seulement si RS + ST = RT.
Calculons donc la mesure, en centimètres, des longueurs RS, ST et RT.
Dans le triangle RSA, rectangle en A, on a, d'après le théorème de Pythagore :
RA2 + AS2 = RS2. D'où : RS2 = 32 + 12 = 10.
De même, dans le triangle BTS, rectangle en B, on a, d'après le théorème de Pythagore :
BS2 + BT2 = ST2. D'où : ST2 = 42 + 12 = 17.
Et, dans le triangle RCT, rectangle en C, on a, d'après le théorème de Pythagore :
RC2 + CT2 = RT2. D'où : RT2 = 72 + 22 = 53.
RS + ST =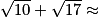 7,285 et RT =
7,285 et RT = 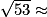 7,2801.
7,2801.
On en déduit que RS + ST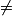 RT et donc que les points R, S et T ne sont pas alignés.
RT et donc que les points R, S et T ne sont pas alignés.
Les points R, S et T sont alignés dans cet ordre si et seulement si RS + ST = RT.
Calculons donc la mesure, en centimètres, des longueurs RS, ST et RT.
Dans le triangle RSA, rectangle en A, on a, d'après le théorème de Pythagore :
RA2 + AS2 = RS2. D'où : RS2 = 32 + 12 = 10.
De même, dans le triangle BTS, rectangle en B, on a, d'après le théorème de Pythagore :
BS2 + BT2 = ST2. D'où : ST2 = 42 + 12 = 17.
Et, dans le triangle RCT, rectangle en C, on a, d'après le théorème de Pythagore :
RC2 + CT2 = RT2. D'où : RT2 = 72 + 22 = 53.
RS + ST =
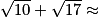 7,285 et RT =
7,285 et RT = 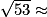 7,2801.
7,2801.On en déduit que RS + ST
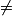 RT et donc que les points R, S et T ne sont pas alignés.
RT et donc que les points R, S et T ne sont pas alignés.• 3e méthode : utilisation du théorème de Thalès
On fait un raisonnement pas l'absurde : si les points R, S et T étaient alignés, comme R, A et C sont alignés et que (AS) et (CT) sont deux droites parallèles, on aurait, d'après le théorème de Thalès :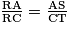 . Or,
. Or, 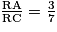 et
et 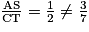 . L'hypothèse d'alignement était donc absurde ; les points R, S et T ne sont pas alignés.
. L'hypothèse d'alignement était donc absurde ; les points R, S et T ne sont pas alignés.
On fait un raisonnement pas l'absurde : si les points R, S et T étaient alignés, comme R, A et C sont alignés et que (AS) et (CT) sont deux droites parallèles, on aurait, d'après le théorème de Thalès :
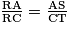 . Or,
. Or, 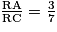 et
et 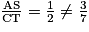 . L'hypothèse d'alignement était donc absurde ; les points R, S et T ne sont pas alignés.
. L'hypothèse d'alignement était donc absurde ; les points R, S et T ne sont pas alignés.Par conséquent, l'affirmation de Camille est fausse.
B. Situation des cinq carrés
1. Mise en équation
La somme des aires des trois carrés gris est :
(n − 2)2 + (n − 1)2 + n2 = n2 − 4n + 4 + n2 − 2n + 1 + n2 = 3n2 − 6n + 5.
La somme des aires des deux carrés blancs est :
(n + 1)2 + (n + 2)2 = n2 + 2n + 1 + n2 + 4n + 4 = 2n2 + 6n + 5.
Les deux sommes sont égales si et seulement si : 3n2 − 6n + 5 = 2n2 + 6n + 5.
C'est-à-dire si : n2 − 12n = 0.
La somme des aires des trois carrés gris est :
(n − 2)2 + (n − 1)2 + n2 = n2 − 4n + 4 + n2 − 2n + 1 + n2 = 3n2 − 6n + 5.
La somme des aires des deux carrés blancs est :
(n + 1)2 + (n + 2)2 = n2 + 2n + 1 + n2 + 4n + 4 = 2n2 + 6n + 5.
Les deux sommes sont égales si et seulement si : 3n2 − 6n + 5 = 2n2 + 6n + 5.
C'est-à-dire si : n2 − 12n = 0.
2. Résolution algébrique
n2 − 12n = 0 si et seulement si n(n − 12) = 0.
Un produit est nul si et seulement si un de ses facteurs est nul ; les solutions sont donc 0 et 12.
n2 − 12n = 0 si et seulement si n(n − 12) = 0.
Un produit est nul si et seulement si un de ses facteurs est nul ; les solutions sont donc 0 et 12.
3. Solutions retenues
Au vu des données du problème, la solution n = 0 correspond à des longueurs de côtés négatives pour les deux premiers carrés ; cette solution doit donc être rejetée.
Seule la solution n = 12 peut donc être retenue.
Au vu des données du problème, la solution n = 0 correspond à des longueurs de côtés négatives pour les deux premiers carrés ; cette solution doit donc être rejetée.
Seule la solution n = 12 peut donc être retenue.
4. Figure à l'échelle 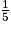
La solution au problème des cinq carrés fournit les longueurs de côté suivantes : 10 cm, 11 cm, 12 cm, 13 cm et 14 cm. À l'échelle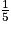 , toutes les longueurs sont divisées par 5. On obtient donc : 2 cm, 2,2 cm, 2,4 cm, 2,6 cm et 2,8 cm.
, toutes les longueurs sont divisées par 5. On obtient donc : 2 cm, 2,2 cm, 2,4 cm, 2,6 cm et 2,8 cm.
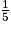
La solution au problème des cinq carrés fournit les longueurs de côté suivantes : 10 cm, 11 cm, 12 cm, 13 cm et 14 cm. À l'échelle
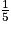 , toutes les longueurs sont divisées par 5. On obtient donc : 2 cm, 2,2 cm, 2,4 cm, 2,6 cm et 2,8 cm.
, toutes les longueurs sont divisées par 5. On obtient donc : 2 cm, 2,2 cm, 2,4 cm, 2,6 cm et 2,8 cm.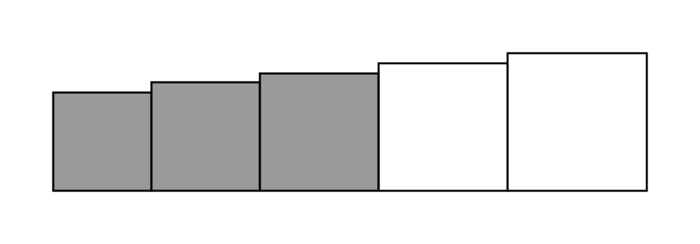 |
C. Situation des sept carrés
1. Résolution graphique
Par lecture graphique, il semble que les courbes aient deux points d'intersection, d'abscisses respectives 3 et 27. Or il faut que la solution soit supérieure ou égale à 7 pour que les côtés de tous les carrés soient de mesures strictement positives ; la solution 3 est donc à rejeter.
Le problème des sept carrés semble avoir une solution, correspondant à x = 27.
Par lecture graphique, il semble que les courbes aient deux points d'intersection, d'abscisses respectives 3 et 27. Or il faut que la solution soit supérieure ou égale à 7 pour que les côtés de tous les carrés soient de mesures strictement positives ; la solution 3 est donc à rejeter.
Le problème des sept carrés semble avoir une solution, correspondant à x = 27.
2. Vérification
Pour x = 27, la somme des aires des carrés gris vaut : 212 + 222 + 232 + 242 = 2 030.
Et la somme des carrés blancs vaut : 252 + 262 + 272 = 2 030.
27 est donc bien solution.
Pour x = 27, la somme des aires des carrés gris vaut : 212 + 222 + 232 + 242 = 2 030.
Et la somme des carrés blancs vaut : 252 + 262 + 272 = 2 030.
27 est donc bien solution.
D. Situation des quatre carrés
1. Feuille de calcul correspondant à chacun des cas
On observe que, dans la feuille de calcul B, les valeurs de la colonne « aire de la partie blanche » sont égales aux valeurs de la colonne « aire du 4e carré » ; on en déduit que la feuille de calcul B correspond au cas 2 et donc que la feuille de calcul A correspond au cas 1.
On observe que, dans la feuille de calcul B, les valeurs de la colonne « aire de la partie blanche » sont égales aux valeurs de la colonne « aire du 4e carré » ; on en déduit que la feuille de calcul B correspond au cas 2 et donc que la feuille de calcul A correspond au cas 1.
2. Feuille de calcul A
a) Formule entrée en E2 et étirée vers le bas
Pour générer la colonne E à partir de la colonne A, on peut taper en E2 : =(A2+3)^2.
Pour générer la colonne E à partir de la colonne A, on peut taper en E2 : =(A2+3)^2.
b) Formule entrée en F2 et étirée vers le bas
Pour générer la colonne F, on peut taper en F2 : =B2+E2.
Pour générer la colonne F, on peut taper en F2 : =B2+E2.
3. Conjectures à partir des feuilles de calcul
• Feuille de calcul A, cas 1
Il semble que l'écart entre l'aire de la partie grise (colonne F) et l'aire de la partie blanche (colonne G) soit toujours égal à 4. Le problème semble ne pas avoir de solution.
Il semble que l'écart entre l'aire de la partie grise (colonne F) et l'aire de la partie blanche (colonne G) soit toujours égal à 4. Le problème semble ne pas avoir de solution.
• Feuille de calcul B, cas 2
L'aire de la partie grise est inférieure à celle de la partie blanche pour un côté du plus petit carré de longueur égale à 1 ; pour une longueur de côté du plus petit carré égale à 2, c'est le contraire, il semble donc qu'il y ait une solution arithmétique dans le cas 2. Le problème posé semble toutefois ne pas avoir de solution, car la solution arithmétique semble non entière.
L'aire de la partie grise est inférieure à celle de la partie blanche pour un côté du plus petit carré de longueur égale à 1 ; pour une longueur de côté du plus petit carré égale à 2, c'est le contraire, il semble donc qu'il y ait une solution arithmétique dans le cas 2. Le problème posé semble toutefois ne pas avoir de solution, car la solution arithmétique semble non entière.
4. Justification de l'absence de solution
Soit x la mesure, en centimètres, de la longueur du petit carré.
Soit x la mesure, en centimètres, de la longueur du petit carré.
• Cas 1
Le problème posé se traduit algébriquement par :
x2 + (x + 3)2 = (x + 1)2 + (x + 2)2, soit 2x2 + 6x + 9 = 2x2 + 6x + 5. D'où : 9 = 5.
Cette équation n'a pas de solution, l'aire de la surface grise ne peut donc être égale à l'aire de la surface blanche dans le cas 1.
Le problème posé se traduit algébriquement par :
x2 + (x + 3)2 = (x + 1)2 + (x + 2)2, soit 2x2 + 6x + 9 = 2x2 + 6x + 5. D'où : 9 = 5.
Cette équation n'a pas de solution, l'aire de la surface grise ne peut donc être égale à l'aire de la surface blanche dans le cas 1.
• Cas 2
Le problème se traduit par :
x2 + (x + 1)2 + (x + 2)2 = (x + 3)2, soit 3x2 + 6x + 5 = x2 + 6x + 9. D'où 2x2 = 4 et finalement : x2 = 2. La seule solution positive de cette équation est : x =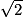 . Cette solution n'est toutefois pas entière.
. Cette solution n'est toutefois pas entière.
Le problème se traduit par :
x2 + (x + 1)2 + (x + 2)2 = (x + 3)2, soit 3x2 + 6x + 5 = x2 + 6x + 9. D'où 2x2 = 4 et finalement : x2 = 2. La seule solution positive de cette équation est : x =
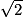 . Cette solution n'est toutefois pas entière.
. Cette solution n'est toutefois pas entière.Au vu des contraintes du problème, il n'y a donc pas de solution dans le cas 2.
Deuxième partie
Exercice 1
Remarque
Pour justifier qu'une affirmation est fausse, on peut, selon les cas, résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, ou encore démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou bien démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
1.
Remarque
Le nombre d'appareils des deux marques n'étant pas le même, on ne peut faire la moyenne des pourcentages d'appareils défectueux ; il faut ici, à partir des données, calculer le nombre d'appareils défectueux, puis le pourcentage que représentent ces appareils en rapport au nombre total d'appareils.• Société 1
Le nombre d'appareils défectueux est :
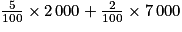 = 240.
= 240.
Cela représente :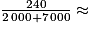 0,027, soit 2,7 % des appareils.
0,027, soit 2,7 % des appareils.
Le nombre d'appareils défectueux est :
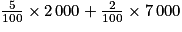 = 240.
= 240.Cela représente :
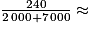 0,027, soit 2,7 % des appareils.
0,027, soit 2,7 % des appareils.• Société 2
Le nombre d'appareils défectueux est :
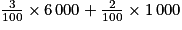 = 200.
= 200.
Cela représente :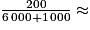 0,029, soit 2,9 % des appareils.
0,029, soit 2,9 % des appareils.
Le nombre d'appareils défectueux est :
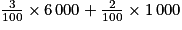 = 200.
= 200.Cela représente :
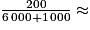 0,029, soit 2,9 % des appareils.
0,029, soit 2,9 % des appareils.Conclusion : l'affirmation est vraie.
2.
• 1re méthode : contre-exemple
Un cube d'arête 1 cm a une aire de 6 cm2 et un volume de 1 cm3.
Un cube d'arête 2 cm a une aire de 24 cm2 et un volume de 8 cm3.
24 = 6 × 4 mais 8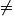 1 × 4. Le volume d'un cube n'est donc pas proportionnel à son aire, car la propriété de linéarité multiplicative n'est pas vérifiée.
1 × 4. Le volume d'un cube n'est donc pas proportionnel à son aire, car la propriété de linéarité multiplicative n'est pas vérifiée.
Conclusion : l'affirmation est fausse.
Un cube d'arête 1 cm a une aire de 6 cm2 et un volume de 1 cm3.
Un cube d'arête 2 cm a une aire de 24 cm2 et un volume de 8 cm3.
24 = 6 × 4 mais 8
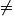 1 × 4. Le volume d'un cube n'est donc pas proportionnel à son aire, car la propriété de linéarité multiplicative n'est pas vérifiée.
1 × 4. Le volume d'un cube n'est donc pas proportionnel à son aire, car la propriété de linéarité multiplicative n'est pas vérifiée.Conclusion : l'affirmation est fausse.
• 2e méthode : cas général
Soit x la mesure de la longueur de l'arête d'un cube. Son aire est alors 6x2 et son volume x3.
La relation entre l'aire et le volume n'est pas de la forme : Volume = k × Aire, avec k constant ; le volume d'un cube n'est donc pas proportionnel à son aire.
Conclusion : l'affirmation est fausse.
Soit x la mesure de la longueur de l'arête d'un cube. Son aire est alors 6x2 et son volume x3.
La relation entre l'aire et le volume n'est pas de la forme : Volume = k × Aire, avec k constant ; le volume d'un cube n'est donc pas proportionnel à son aire.
Conclusion : l'affirmation est fausse.
3. 1 m3 = 1 000 L donc 0,3 m3 = 300 L.
Il faut 15 L par m2. Donc, pour arroser quatre fois un potager de 5 m2, il faut :
15 L × 5 × 4 = 300 L d'eau.
Conclusion : l'affirmation est vraie.
Il faut 15 L par m2. Donc, pour arroser quatre fois un potager de 5 m2, il faut :
15 L × 5 × 4 = 300 L d'eau.
Conclusion : l'affirmation est vraie.
4. A = 7 + 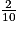 = 7,2. Donc A2 = 51,84. La partie décimale de A2 est 0,84 (ou
= 7,2. Donc A2 = 51,84. La partie décimale de A2 est 0,84 (ou 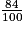 ).
).
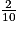 = 7,2. Donc A2 = 51,84. La partie décimale de A2 est 0,84 (ou
= 7,2. Donc A2 = 51,84. La partie décimale de A2 est 0,84 (ou 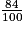 ).
).Remarque
Attention : la partie décimale n'est pas 84 !Conclusion : l'affirmation est fausse.
Exercice 2
Le tirage est supposé équiprobable (bien que cela ne soit pas dit ainsi, mais l'énoncé évoque un dé « équilibré »).
1.
a) Nombre d'obtentions du « 6 »
200 − (30 + 41 + 32 + 28 + 31) = 200 − 162 = 38.
Inès a obtenu 38 fois le « 6 ».
200 − (30 + 41 + 32 + 28 + 31) = 200 − 162 = 38.
Inès a obtenu 38 fois le « 6 ».
b) Fréquence d'apparition du « 1 »
On a :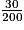 = 0,15.
= 0,15.
La fréquence d'apparition du « 1 » est 15 %.
On a :
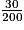 = 0,15.
= 0,15.La fréquence d'apparition du « 1 » est 15 %.
2.
a) Probabilité d'obtenir deux nombres dont le produit est égal à 9
La seule décomposition multiplicative de 9 avec des facteurs inférieurs ou égaux à 6 est : 3 × 3.
Il y a 6 × 6 = 36 issues possibles lorsqu'on lance deux dés à 6 faces et une seule issue correspond à obtenir deux « 3 ».
La probabilité d'obtenir deux nombres dont le produit est égal à 9 est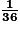 .
.
La seule décomposition multiplicative de 9 avec des facteurs inférieurs ou égaux à 6 est : 3 × 3.
Il y a 6 × 6 = 36 issues possibles lorsqu'on lance deux dés à 6 faces et une seule issue correspond à obtenir deux « 3 ».
La probabilité d'obtenir deux nombres dont le produit est égal à 9 est
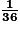 .
.b) Probabilité d'obtenir deux nombres dont le produit est égal à 12
Les décompositions multiplicatives de 12 sont : 2 × 6 et 3 × 4. Il y a donc quatre issues favorables : obtenir 2 et 6, obtenir 6 et 2, obtenir 3 et 4, et obtenir 4 et 3.
La probabilité d'obtenir deux nombres dont le produit est égal à 12 est donc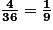 .
.
Les décompositions multiplicatives de 12 sont : 2 × 6 et 3 × 4. Il y a donc quatre issues favorables : obtenir 2 et 6, obtenir 6 et 2, obtenir 3 et 4, et obtenir 4 et 3.
La probabilité d'obtenir deux nombres dont le produit est égal à 12 est donc
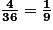 .
.Exercice 3
1. Nature des figures tracées en exécutant les programmes
Le programme A permet de tracer un carré de côté 100 ; le programme B permet de tracer un triangle équilatéral de côté 100.
Le programme A permet de tracer un carré de côté 100 ; le programme B permet de tracer un triangle équilatéral de côté 100.
2.
a) Angle d'un pentagone régulier
D'après la formule donnée dans l'énoncé, la somme des angles du pentagone régulier vaut :
180° × 5 − 360° = 540°.
Tous les angles du pentagone étant égaux, on en déduit que :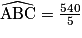 = 108°.
= 108°.
Or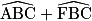 = 180°, d'où :
= 180°, d'où : 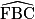 = 180° − 108° = 72°.
= 180° − 108° = 72°.
On a donc bien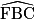 = 72°.
= 72°.
D'après la formule donnée dans l'énoncé, la somme des angles du pentagone régulier vaut :
180° × 5 − 360° = 540°.
Tous les angles du pentagone étant égaux, on en déduit que :
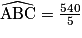 = 108°.
= 108°.Or
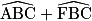 = 180°, d'où :
= 180°, d'où : 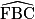 = 180° − 108° = 72°.
= 180° − 108° = 72°.On a donc bien
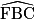 = 72°.
= 72°.b) Modifications à apporter au programme A
Il faut remplacer « répéter 4 fois » par « répéter 5 fois », et « tourner de 90 degrés » par « tourner de 72 degrés ».
Il faut remplacer « répéter 4 fois » par « répéter 5 fois », et « tourner de 90 degrés » par « tourner de 72 degrés ».
3. Choix du programme pour tracer un pentagone régulier à n côtés
Le programme 2 convient.
Le programme 1 ne convient pas car il ne permet pas de choisir le nombre de côtés du pentagone tracé : il trace toujours un décagone.
Le programme 3 ne convient pas car la mesure angulaire ne tient pas compte du nombre de côtés choisi : si on choisit 10 côtés, on obtiendra bien un décagone régulier ; sinon, on obtient une ligne brisée à n segments (n étant le nombre de « côtés » choisi).
Le programme 2 convient.
Le programme 1 ne convient pas car il ne permet pas de choisir le nombre de côtés du pentagone tracé : il trace toujours un décagone.
Le programme 3 ne convient pas car la mesure angulaire ne tient pas compte du nombre de côtés choisi : si on choisit 10 côtés, on obtiendra bien un décagone régulier ; sinon, on obtient une ligne brisée à n segments (n étant le nombre de « côtés » choisi).
Remarque
Si le nombre de côtés est un multiple de 10, on obtient un décagone régulier.Le programme 4 ne convient pas non plus car l'angle est erroné : 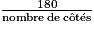 au lieu de
au lieu de 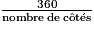 .
.
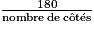 au lieu de
au lieu de 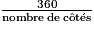 .
.4. Tracé d'un cercle avec Scratch
Un cercle étant la limite d'un polygone avec un nombre de côtés que l'on fait tendre vers l'infini, pour construire une figure ayant l'apparence d'un cercle à l'écran, il suffit de choisir un nombre de côtés suffisamment grand : 30, par exemple.
Un cercle étant la limite d'un polygone avec un nombre de côtés que l'on fait tendre vers l'infini, pour construire une figure ayant l'apparence d'un cercle à l'écran, il suffit de choisir un nombre de côtés suffisamment grand : 30, par exemple.
Troisième partie
Situation 1
1. Usage du nombre mobilisé
L'usage du nombre mobilisé ici est « le nombre pour garder la mémoire de la quantité ».
L'usage du nombre mobilisé ici est « le nombre pour garder la mémoire de la quantité ».
2. Intérêt du quai
Le quai permet aux élèves de différer la correspondance terme à terme qui sert de validation et ainsi de percevoir l'(in)égalité des cardinaux de la collection des places vides et de la collection des jetons ramenés avant vérification par correspondance terme à terme : une place = un jeton.
Le quai permet aux élèves de différer la correspondance terme à terme qui sert de validation et ainsi de percevoir l'(in)égalité des cardinaux de la collection des places vides et de la collection des jetons ramenés avant vérification par correspondance terme à terme : une place = un jeton.
3. Analyse des procédures des élèves au regard des acquis liés à la notion de nombre
Il est à noter en préambule que tous les élèves ont réussi.
L'élève A a estimé le nombre de places vides et a ramené plus de jetons que nécessaire. Il a ensuite distribué les jetons en fonction des places libres, puis rapporté les jetons surnuméraires. Cet élève n'a donc pas dénombré les places vides.
L'élève B semble avoir dénombré les places vides, puis les jetons nécessaires.
L'élève C a réalisé une correspondance terme à terme entre place vide et jeton… et a donc effectué autant de voyages qu'il y a de places vides.
L'élève D semble avoir dénombré les places vides, puis les jetons nécessaires, en décomposant toutefois le nombre en 4 et 3, 4 correspondant au nombre de places vides dans la colonne de gauche et 3 correspondant au nombre de places vides dans la colonne de droite.
Il est à noter en préambule que tous les élèves ont réussi.
L'élève A a estimé le nombre de places vides et a ramené plus de jetons que nécessaire. Il a ensuite distribué les jetons en fonction des places libres, puis rapporté les jetons surnuméraires. Cet élève n'a donc pas dénombré les places vides.
L'élève B semble avoir dénombré les places vides, puis les jetons nécessaires.
L'élève C a réalisé une correspondance terme à terme entre place vide et jeton… et a donc effectué autant de voyages qu'il y a de places vides.
L'élève D semble avoir dénombré les places vides, puis les jetons nécessaires, en décomposant toutefois le nombre en 4 et 3, 4 correspondant au nombre de places vides dans la colonne de gauche et 3 correspondant au nombre de places vides dans la colonne de droite.
4. Modifications de la tâche pour que les élèves A et C fassent évoluer leur procédure
L'enseignante qui souhaite que les élèves A et C dénombrent les places vides peut :
L'enseignante qui souhaite que les élèves A et C dénombrent les places vides peut :
- demander aux élèves de ne faire qu'un seul voyage (ce qui bloque les procédures des élèves A et C et leur demande donc d'en trouver d'autres) ;
- réduire la quantité de places vides (ce qui permet de se placer dans un champ numérique que les élèves savent dénombrer) ;
- modifier l'organisation spatiale des places vides pour permettre la reconnaissance d'une constellation connue.
Situation 2
Remarque
On peut très bien, ici, traiter les deux questions en parallèle, du moment que l'on sépare les réponses.1. et 2. Analyse des productions d'élèves au regard des connaissances mobilisées sur les nombres et sur les propriétés des opérations et différences entre les productions
Il est à noter que tous les résultats sont justes et que tous les élèves calculent en ligne.
Il est à noter que tous les résultats sont justes et que tous les élèves calculent en ligne.
• Calcul 1
L'élève 1 utilise l'écriture décimale des nombres et la propriété des écarts constants : il retranche d'abord 6 à chacun des termes, puis 0,42 à chacun des nouveaux termes obtenus.
L'élève 2 utilise la désignation verbale des nombres donnée par l'enseignant et exprime dans un premier temps le premier terme en centièmes et le second en dixièmes, avant de convertir le second terme en centièmes également. Il opère ensuite sur des nombres entiers de centièmes en utilisant également la propriété des écarts constants pour ajouter 20 à chacun des deux termes, ce qui lui permet d'avoir un second terme multiple de 100, et donc facile à retrancher mentalement. Il donne la réponse en centièmes et sous forme partiellement textuelle.
Différences :
L'élève 1 utilise l'écriture décimale des nombres et la propriété des écarts constants : il retranche d'abord 6 à chacun des termes, puis 0,42 à chacun des nouveaux termes obtenus.
L'élève 2 utilise la désignation verbale des nombres donnée par l'enseignant et exprime dans un premier temps le premier terme en centièmes et le second en dixièmes, avant de convertir le second terme en centièmes également. Il opère ensuite sur des nombres entiers de centièmes en utilisant également la propriété des écarts constants pour ajouter 20 à chacun des deux termes, ce qui lui permet d'avoir un second terme multiple de 100, et donc facile à retrancher mentalement. Il donne la réponse en centièmes et sous forme partiellement textuelle.
Différences :
- la désignation des nombres utilisée : décimale pour l'un, verbale pour l'autre ;
- l'usage fait de la propriété des écarts constants.
• Calcul 2
Remarque : on ne sait pas sous quelle forme le calcul a été communiqué aux élèves, contrairement au calcul 1, où cela était précisé.
L'élève 3 utilise l'écriture décimale des nombres, décompose (mentalement) 15 en 10 + 5, puis utilise la distributivité de la multiplication sur l'addition. Après avoir effectué mentalement 10 × 0,24 et 5 × 0,24, il additionne les deux nombres. Il est probable que le résultat de 5 × 0,24 ait été obtenu en divisant par deux le résultat de 10 × 0,24 et donc en utilisant le résultat 5 = 10 ÷ 2 et l'associativité de la multiplication.
L'élève 4 transcrit 0,24 sous forme verbale. Il opère sur des entiers en décomposant mentalement 24 en 20 + 4, calculant mentalement le produit de 15 par 20, puis par 4 et additionnant les deux résultats partiels. Il utilise également, ce faisant, la distributivité de la multiplication sur l'addition.
Différences :
Remarque : on ne sait pas sous quelle forme le calcul a été communiqué aux élèves, contrairement au calcul 1, où cela était précisé.
L'élève 3 utilise l'écriture décimale des nombres, décompose (mentalement) 15 en 10 + 5, puis utilise la distributivité de la multiplication sur l'addition. Après avoir effectué mentalement 10 × 0,24 et 5 × 0,24, il additionne les deux nombres. Il est probable que le résultat de 5 × 0,24 ait été obtenu en divisant par deux le résultat de 10 × 0,24 et donc en utilisant le résultat 5 = 10 ÷ 2 et l'associativité de la multiplication.
L'élève 4 transcrit 0,24 sous forme verbale. Il opère sur des entiers en décomposant mentalement 24 en 20 + 4, calculant mentalement le produit de 15 par 20, puis par 4 et additionnant les deux résultats partiels. Il utilise également, ce faisant, la distributivité de la multiplication sur l'addition.
Différences :
- la désignation des nombres utilisée : décimale pour l'un, verbale pour l'autre ;
- l'usage fait de la propriété de distributivité de la multiplication sur l'addition.
Situation 3
1. Notion travaillée
La notion travaillée ici est la proportionnalité. Le nombre d'œufs est proportionnel au nombre de convives.
La notion travaillée ici est la proportionnalité. Le nombre d'œufs est proportionnel au nombre de convives.
2. Analyse des productions et procédures des élèves
L'élève A utilise explicitement la linéarité additive en observant que le nombre de convives évoqué dans la question est la somme des nombres de convives pour lesquels l'information sur le nombre d'œufs correspondant est donnée. Il effectue les calculs en ligne.
L'élève B utilise la même propriété sans l'expliciter, mais en représentant les convives évoqués à chaque étape, ce qui ne fournit en rien la réponse au problème posé. Il écrit en regard les correspondances nombre de convives/nombre d'œufs. Il pose les additions.
L'élève C utilise la linéarité multiplicative pour calculer le nombre d'œufs pour 5 personnes à partir de celui prévu pour 10 personnes (ce calcul est fait mentalement), puis additionne trois fois le résultat obtenu (calcul en ligne) et utilise, ce faisant, la linéarité additive.
L'élève D observe le rapport entre nombre d'œufs et nombre de personnes et en déduit le nombre de personnes correspondant à un œuf (retour à l'unité), puis en déduit le nombre de personnes correspondant à 3 œufs en utilisant la linéarité multiplicative.
L'élève A utilise explicitement la linéarité additive en observant que le nombre de convives évoqué dans la question est la somme des nombres de convives pour lesquels l'information sur le nombre d'œufs correspondant est donnée. Il effectue les calculs en ligne.
L'élève B utilise la même propriété sans l'expliciter, mais en représentant les convives évoqués à chaque étape, ce qui ne fournit en rien la réponse au problème posé. Il écrit en regard les correspondances nombre de convives/nombre d'œufs. Il pose les additions.
L'élève C utilise la linéarité multiplicative pour calculer le nombre d'œufs pour 5 personnes à partir de celui prévu pour 10 personnes (ce calcul est fait mentalement), puis additionne trois fois le résultat obtenu (calcul en ligne) et utilise, ce faisant, la linéarité additive.
L'élève D observe le rapport entre nombre d'œufs et nombre de personnes et en déduit le nombre de personnes correspondant à un œuf (retour à l'unité), puis en déduit le nombre de personnes correspondant à 3 œufs en utilisant la linéarité multiplicative.
3. Progressivité dans l'apprentissage de la notion
Les trois énoncés se situent dans le même contexte. Pour répondre, l'élève doit observer les relations arithmétiques entre les données (entières) de l'énoncé. Le choix fait sur ces données favorise certaines procédures et les fait évoluer.
Dans l'exercice 1, le nombre de personnes est la somme du nombre de personnes en jeu dans les deux recettes évoquées dans l'énoncé. L'utilisation de la linéarité additive est donc fortement encouragée, même si d'autres procédures sont possibles.
Dans l'exercice 2, les nombres en relation ont toujours un diviseur commun, ce qui facilite l'utilisation de la linéarité multiplicative, même si l'usage partiel de la linéarité additive reste possible, ce que fait d'ailleurs l'élève C. En revanche, le passage à l'unité ne fait pas sens dans le contexte de l'exercice.
Dans l'exercice 3, le rapport : (nombre de personnes) / (nombre d'œufs) est facile à percevoir et entier, ce qui favorise le passage à l'unité, alors que l'utilisation de la linéarité multiplicative, pour passer directement de 5 à 3 œufs, n'est pas possible pour des élèves de CM. On pourrait toutefois utiliser la linéarité multiplicative pour calculer le nombre de personnes correspondant à 15 œufs et en déduire celui correspondant à 3 œufs…
Les trois énoncés se situent dans le même contexte. Pour répondre, l'élève doit observer les relations arithmétiques entre les données (entières) de l'énoncé. Le choix fait sur ces données favorise certaines procédures et les fait évoluer.
Dans l'exercice 1, le nombre de personnes est la somme du nombre de personnes en jeu dans les deux recettes évoquées dans l'énoncé. L'utilisation de la linéarité additive est donc fortement encouragée, même si d'autres procédures sont possibles.
Dans l'exercice 2, les nombres en relation ont toujours un diviseur commun, ce qui facilite l'utilisation de la linéarité multiplicative, même si l'usage partiel de la linéarité additive reste possible, ce que fait d'ailleurs l'élève C. En revanche, le passage à l'unité ne fait pas sens dans le contexte de l'exercice.
Dans l'exercice 3, le rapport : (nombre de personnes) / (nombre d'œufs) est facile à percevoir et entier, ce qui favorise le passage à l'unité, alors que l'utilisation de la linéarité multiplicative, pour passer directement de 5 à 3 œufs, n'est pas possible pour des élèves de CM. On pourrait toutefois utiliser la linéarité multiplicative pour calculer le nombre de personnes correspondant à 15 œufs et en déduire celui correspondant à 3 œufs…
4. Proposition d'exercice complémentaire
Pour poursuivre l'apprentissage, l'enseignant pourrait proposer un énoncé où les nombres n'ont pas de relation arithmétique simple entre eux, avec, par exemple, une valeur unitaire décimale (mais simple).
« Ma recette de crème à la vanille dit que je dois mélanger 15 g de sucre vanillé avec 6 œufs. J'ai 10 œufs chez moi, que j'aimerais tous utiliser pour faire de la crème vanille. Combien de sucre vanillé dois-je ajouter ? »
Pour poursuivre l'apprentissage, l'enseignant pourrait proposer un énoncé où les nombres n'ont pas de relation arithmétique simple entre eux, avec, par exemple, une valeur unitaire décimale (mais simple).
« Ma recette de crème à la vanille dit que je dois mélanger 15 g de sucre vanillé avec 6 œufs. J'ai 10 œufs chez moi, que j'aimerais tous utiliser pour faire de la crème vanille. Combien de sucre vanillé dois-je ajouter ? »
Document précédent
Sujet 2020, groupement académique 3
Document suivant
Sujet 2019, groupement académique 2
