Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
A. Boîte de sauce tomate
Un fabricant de sauce tomate utilise des boîtes de conserve de forme cylindrique de diamètre 99 mm et de hauteur 118 mm.
Le format de ces boîtes est appelé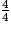 .
.
Le format de ces boîtes est appelé
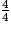 .
. |
| Rappel du volume d'un cylindre : V = Aire de la base × hauteur |
Dans tout cet exercice, on négligera l'épaisseur du métal.
1. Calculer le volume, en cm3, d'une boîte de conserve 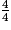 . Arrondir le résultat à l'unité.
. Arrondir le résultat à l'unité.
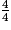 . Arrondir le résultat à l'unité.
. Arrondir le résultat à l'unité.2. La contenance affichée sur la boîte est 850 mL. Vérifier qu'une boîte remplie à 95 % contient bien au moins 850 mL de sauce tomate.
3. On considère une nouvelle boîte de même hauteur et dont le diamètre est le double de la précédente. Le volume de la nouvelle boîte est-il le double du volume d'une boîte 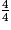 ? Justifier la réponse.
? Justifier la réponse.
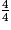 ? Justifier la réponse.
? Justifier la réponse.4. On considère une autre boîte de conserve de diamètre 73 mm et de hauteur 54 mm. Le format de cette boîte s'appelle 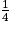 . Calculer le volume de cette boîte cylindrique arrondi au cm3, puis justifier l'appellation du format
. Calculer le volume de cette boîte cylindrique arrondi au cm3, puis justifier l'appellation du format 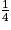 .
.
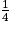 . Calculer le volume de cette boîte cylindrique arrondi au cm3, puis justifier l'appellation du format
. Calculer le volume de cette boîte cylindrique arrondi au cm3, puis justifier l'appellation du format 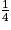 .
.B. Minimisation du coût de fabrication d'une boîte de conserve
Le fabricant doit produire des boîtes de conserve cylindriques de volume fixé 908 cm3. Il souhaite minimiser le coût du métal. Pour cela, il cherche à minimiser l'aire totale A de la boîte : celle-ci correspond à la somme de l'aire des disques de base et de l'aire de la surface latérale du cylindre. Il étudie l'évolution de l'aire de métal totale A, en centimètres carrés, en fonction du rayon r, en centimètres, du disque de base.
1. Dessiner à main levée un patron d'une boîte de conserve cylindrique en repassant de la même couleur les éléments de même longueur.
2. Sachant que le volume de la boîte est de 908 cm3, donner l'expression de la hauteur h, exprimée en centimètres, de la boîte en fonction du rayon r.
3. Pour calculer l'aire totale des cylindres de rayons différents, on a construit à l'aide d'un tableur la feuille de calcul suivante :
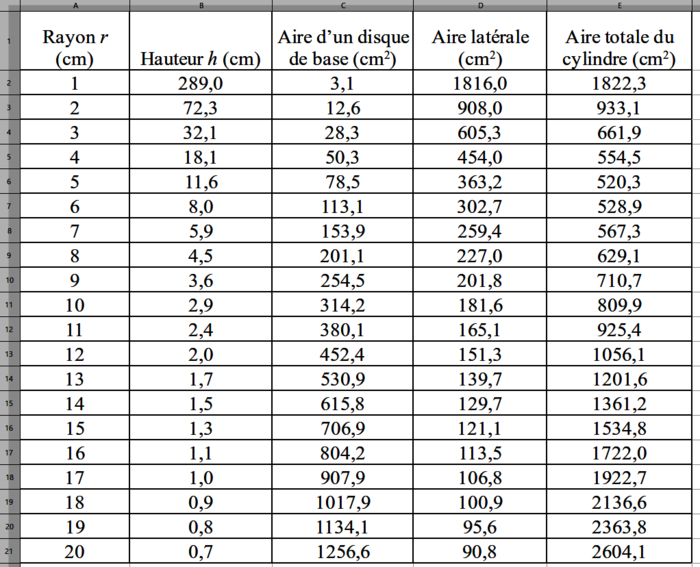 |
a) Sans justifier, parmi les cinq propositions données ci-dessous, recopier celle qui a été saisie dans la cellule C2 et étirée vers le bas jusqu'à la cellule C21.
Proposition 1 : =PI()*A1*A1
Proposition 2 : =PI()*A2*A2
Proposition 3 : =PI()*49,5*49,5
Proposition 4 : =PI()*1*1
Proposition 5 : =PI()*B2*B2
Rappel : « PI() » correspond à la valeur du nombre π.
Proposition 1 : =PI()*A1*A1
Proposition 2 : =PI()*A2*A2
Proposition 3 : =PI()*49,5*49,5
Proposition 4 : =PI()*1*1
Proposition 5 : =PI()*B2*B2
Rappel : « PI() » correspond à la valeur du nombre π.
b) On suppose que les colonnes A, B, C et D sont déjà remplies. Proposer une formule à saisir dans la cellule E2 et copiée par glissement vers le bas jusqu'à la cellule E21, donnant l'aire totale du cylindre.
c) En utilisant la feuille de calcul ci-dessus, conjecturer un encadrement d'amplitude minimale du rayon, correspondant au coût minimal de métal pour la fabrication de cette boîte de conserve.
4. Pour affiner la précision, on a représenté graphiquement, ci-dessous, l'aire totale A en fonction du rayon r.
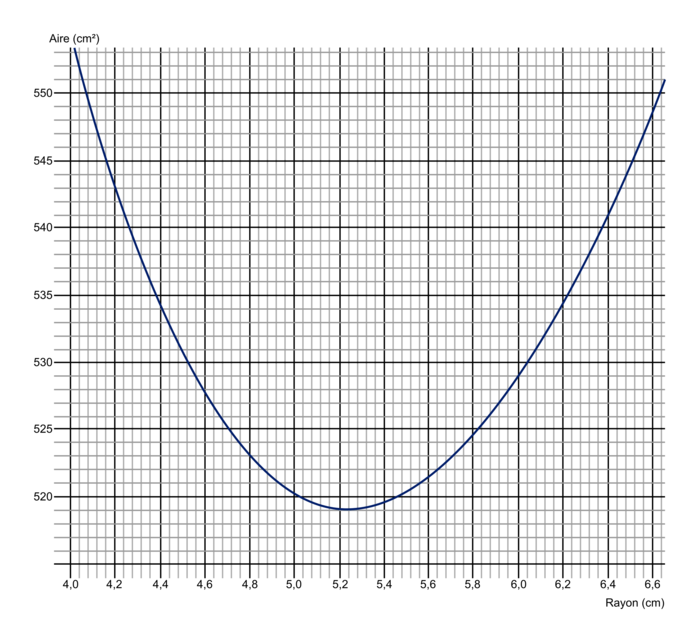 |
Répondre aux questions a) à e) par lecture graphique.
a) L'aire totale A est-elle proportionnelle au rayon r ? Justifier.
b) Déterminer l'aire totale pour un rayon de 4,24 cm.
c) Déterminer les rayons correspondant à une aire totale de 530 cm2.
d) Déterminer l'aire totale minimale.
e) Donner le rayon correspondant.
f) Déterminer, par un calcul, la hauteur correspondante. Arrondir au millimètre.
C. Livraison des boîtes
Le fabricant de sauce tomate souhaite expédier par carton ses boîtes de conserve modèle 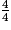 de diamètre 99 mm, de hauteur 118 mm et de masse 880 g. Il a le choix entre les 3 types de cartons ci-dessous (les boîtes sont posées sur leur base dans les cartons) :
de diamètre 99 mm, de hauteur 118 mm et de masse 880 g. Il a le choix entre les 3 types de cartons ci-dessous (les boîtes sont posées sur leur base dans les cartons) :
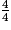 de diamètre 99 mm, de hauteur 118 mm et de masse 880 g. Il a le choix entre les 3 types de cartons ci-dessous (les boîtes sont posées sur leur base dans les cartons) :
de diamètre 99 mm, de hauteur 118 mm et de masse 880 g. Il a le choix entre les 3 types de cartons ci-dessous (les boîtes sont posées sur leur base dans les cartons) :| Carton 1 | Carton 2 | Carton 3 |
|---|---|---|
| Un seul étage contenant 5 boîtes en longueur et 5 boîtes en largeur. | Trois étages contenant chacun 4 boîtes en longueur et 2 boîtes en largeur. | Trois étages contenant chacun 3 boîtes en longueur et 3 boîtes en largeur. |
Le transporteur lui impose deux conditions :
- La masse du carton ne doit pas dépasser 22 kg.
- La somme des dimensions longueur + largeur + hauteur ne doit pas dépasser 100 cm.
Deuxième partie (13 points)
Cette partie est composée de trois exercices indépendants.
Exercice 1
Un couple souhaite aménager les combles de sa maison, représentés par la partie grisée du schéma ci-dessous.
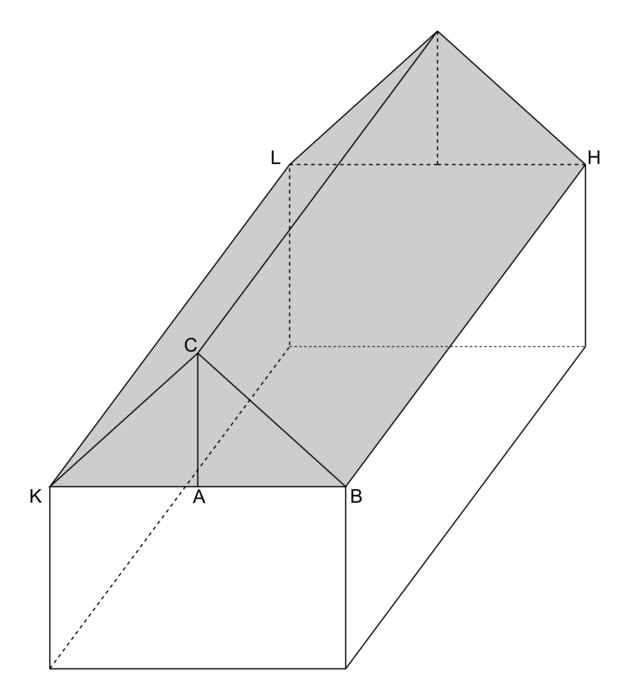 |
KBHL est un rectangle et le point A est le milieu de [BK].
Le triangle ABC ci-dessous représente une coupe de profil d'une partie des combles.
Le triangle ABC ci-dessous représente une coupe de profil d'une partie des combles.
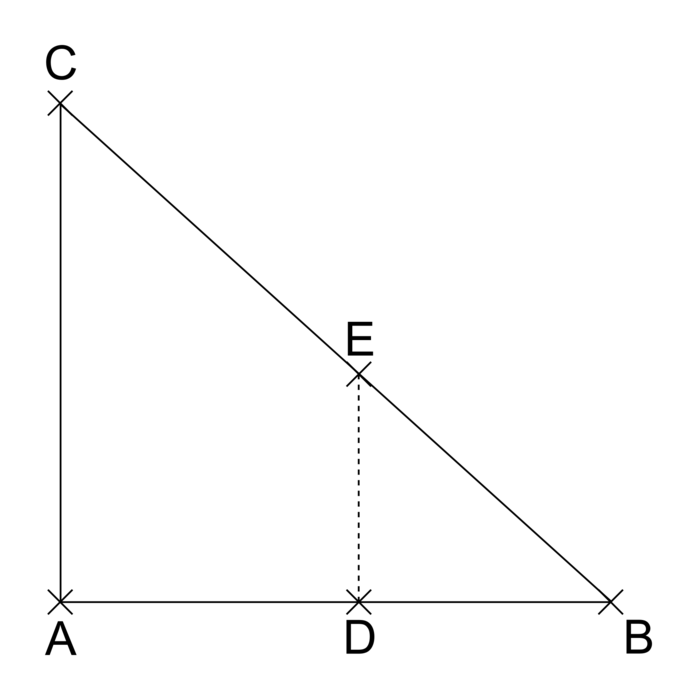 |
On donne les informations suivantes :
- la droite (AC) est perpendiculaire à la droite (AB) ;
- AB = 432 cm et AC = 390 cm ;
- les points D et E sont tels que D appartient au segment [AB], E appartient au segment [BC], la droite (DE) est perpendiculaire à la droite (AB) et DE = 1,80 m.
1. Démontrer que BC = 5,82 m.
2.
Le couple cherche à connaître la superficie Carrez des combles, c'est-à-dire la surface pour laquelle la hauteur sous plafond est supérieure ou égale à 1,80 m.
a) Le segment [DE], perpendiculaire au sol, représente une hauteur sous plafond de 1,80 m. À quelle distance du point A, arrondie au centimètre, se trouve le point D ?
b) La longueur [BH] de la maison mesure 20 m. En déduire la superficie Carrez des combles, arrondie au mètre carré.
Exercice 2
Lors d'un vide-greniers, les organisateurs proposent aux visiteurs d'acheter des tickets de tombola.
Le prix d'un ticket est fixé à deux euros. 4 000 tickets ont été imprimés et vendus.
Les lots ont tous été achetés par les organisateurs.
La répartition des tickets et des lots est donnée par l'extrait de tableur suivant :
Isabelle achète un ticket de tombola.
Le prix d'un ticket est fixé à deux euros. 4 000 tickets ont été imprimés et vendus.
Les lots ont tous été achetés par les organisateurs.
La répartition des tickets et des lots est donnée par l'extrait de tableur suivant :
| Nombre de tickets gagnants | Lot | Valeur du lot |
|---|---|---|
| 1 | Téléviseur | 899 € |
| 5 | Lecteur Blu-ray | 250 € |
| 10 | Smartphone | 125 € |
| 14 | Bracelet connecté | 59 € |
| 30 | Grille-pain | 15 € |
| 100 | Peluche | 0,50 € |
| | Ticket perdant | 0 € |
Isabelle achète un ticket de tombola.
1. Vérifier que la probabilité qu'elle gagne un lot est de 0,04.
2. Quelle est la probabilité qu'lsabelle gagne une peluche ? Donner la réponse sous la forme d'une fraction irréductible, puis d'un pourcentage.
3. Déterminer la probabilité qu'elle gagne un lot dont la valeur est au moins 100 €.
4. En ne considérant que les tickets gagnants, calculer la valeur moyenne d'un lot. On donnera la valeur arrondie au centime.
5. On considère que l'achat des lots est le seul coût engagé. Quelle somme d'argent a rapporté cette tombola ?
6. L'organisateur de la tombola propose un deuxième tirage aux personnes ayant obtenu un ticket perdant. Il leur est proposé de choisir une carte parmi trois. Une de ces trois cartes permet de gagner un lot publicitaire. Quelle est la probabilité qu'une personne ayant acheté un ticket gagne un lot publicitaire ?
Exercice 3
Voici deux programmes de calcul, le premier est codé avec le logiciel Scratch :
Programme A
 |
Programme B
|
1. Vérifier que le nombre 10, appliqué au programme A, permet d'obtenir 20.
2. Quel résultat obtient-on en appliquant le nombre 5,2 au programme B ?
3. En appliquant un même nombre de départ, les programmes A et B peuvent-ils donner un résultat identique ?
4. Déterminer le ou les nombres que l'on doit choisir au départ pour obtenir 0 comme résultat avec le programme A.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Une enseignante propose, en cycle 3, le calcul 13,25 × 10.
Voici les réponses proposées par quatre élèves :
a) 1,325.
b) 130,25.
c) 13,250.
d) 132,5.
Voici les réponses proposées par quatre élèves :
a) 1,325.
b) 130,25.
c) 13,250.
d) 132,5.
1. Analyser les réponses erronées proposées par les élèves en cherchant à expliciter les erreurs qui ont pu conduire les élèves à proposer ces réponses.
2. À la demande de l'enseignante, les élèves proposent une trace écrite de la multiplication d'un nombre décimal par 10.
| Élève 1 : Pour multiplier par 10, on ajoute un zéro à droite du nombre. Élève 2 : Pour multiplier par 10, on déplace la virgule d'un rang vers la droite. |
a) Expliquer pourquoi ces deux propositions ne peuvent pas être retenues par l'enseignante pour être notées dans les cahiers des élèves.
b) Proposer une institutionnalisation que l'enseignante pourrait faire noter dans les cahiers des élèves pour la multiplication d'un nombre décimal par 10.
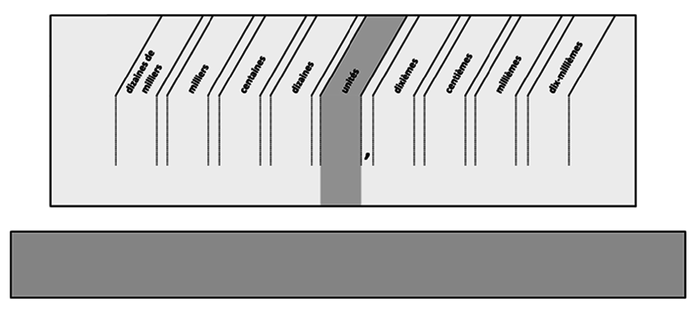
3. En s'appuyant sur l'extrait de la ressource d'accompagnement du programme de mathématiques (cycle 3, EDUSCOL, Fractions et nombres décimaux au cycle 3, annexe 4), l'enseignante propose l'utilisation d'un glisse-nombre dont une utilisation est montrée ci-après. Il est composé d'une languette sur laquelle on écrit les chiffres d'un nombre donné, que l'on peut ensuite faire glisser de façon à faire changer les chiffres de colonne.
 |
 |
En quoi cet outil peut-il aider les élèves ayant donné les réponses a), b) et c) ?
Situation 2
Voici un extrait de la note de service n° 2018-052 du 25 avril 2018 « La résolution de problèmes à l'école élémentaire ».
« Modéliser » et « calculer » sont deux compétences fondamentales pour la résolution de problèmes à l'école élémentaire qui doivent guider l'action de l'enseignant pour aider les élèves à surmonter leurs difficultés. En effet, lors de la résolution de problèmes, les principales difficultés rencontrées peuvent relever de :
|
Un enseignant propose à ses élèves de CM2 le problème suivant :
« Théo achète un pain à 2,35 € et deux viennoiseries valant chacune 1,15 €. Il donne un billet de 10 € au vendeur. Combien le vendeur va-t-il rendre à Théo ? »
Voici les réponses proposées par quatre élèves :
« Théo achète un pain à 2,35 € et deux viennoiseries valant chacune 1,15 €. Il donne un billet de 10 € au vendeur. Combien le vendeur va-t-il rendre à Théo ? »
Voici les réponses proposées par quatre élèves :
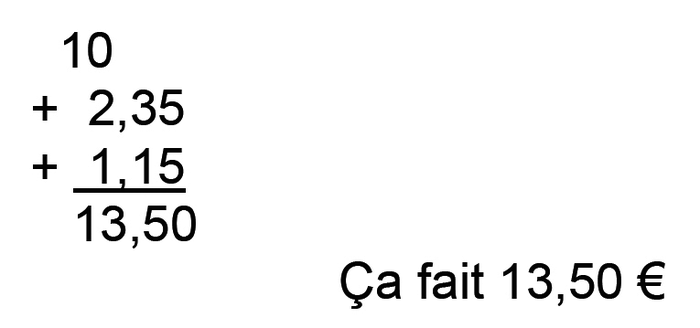 |
 |
 |
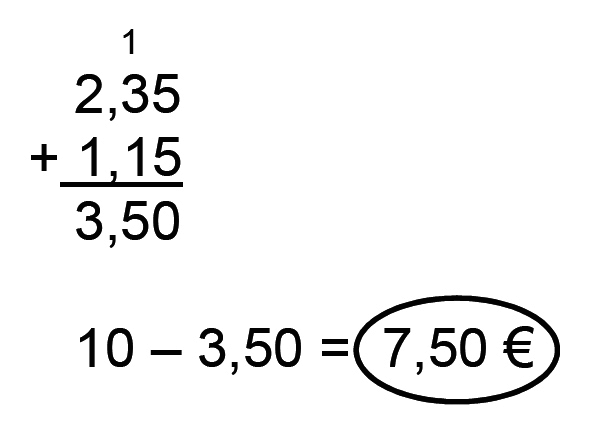 |
1. En vous appuyant sur l'extrait de la note de service proposé ci-dessus, analyser les quatre propositions d'élèves en termes de réussites et d'échecs pour chacune des compétences « modéliser » et « calculer ».
2. Proposer deux activités de remédiation que vous pourriez envisager pour aider l'élève A à réussir ce type de problème, une avec du matériel et une sans matériel.
3. Que peut proposer l'enseignant à l'élève B pour qu'il puisse repérer son erreur ?
4. On considère maintenant le problème suivant : « Théo achète un pain à 2,50 €. Il donne un billet de 10 € au vendeur. Combien le vendeur va-t-il rendre à Théo ? » En comparant les deux problèmes, donner une difficulté qu'un enseignant ne peut pas détecter en proposant ce problème à une étape.
Situation 3
Dans une classe de grande section, un enseignant propose à un groupe d'élèves de retrouver l'image correspondant à la description qu'il énonce.
| Donnez-moi l'image où : A) Le koala est devant la tour de cubes. B) La princesse est derrière le cube. C) Le koala est sur le cube. D) Le koala est entre les deux tours de cubes. E) Le koala est sous le pont de cubes. |
 |
Le tableau ci-dessous répertorie les différentes réponses données par les élèves.
| Affirmations proposées | Réponses des élèves |
|---|---|
| A) Le koala est devant la tour de cubes. | 1 et 7 |
| B) La princesse est derrière le cube. | 5 |
| C) Le koala est sur le cube. | 6, 8 et 3 |
| D) Le koala est entre les deux tours de cubes. | 2 et 4 |
| E) Le koala est sous le pont de cubes. | 2 et 6 |
1. Donner un intérêt et une limite de cette situation.
2. Analyser chacune des réponses données aux affirmations C et E.
3. Tous les élèves de la classe ont réussi à donner l'image de l'assertion B. Que peut-on en conclure ?
4. Un élève fait correspondre l'image 7 à l'affirmation A en justifiant : « Le koala regarde la tour. Il est devant. ». L'enseignant propose la manipulation des objets considérés. Justifier le choix de l'enseignant.
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Boîte de sauce tomate
1. Volume d'une boîte de format 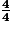
Vboîte 4/4 = Airebase × hauteur = πr2 × h = π ×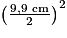 × 11,8 cm
× 11,8 cm  908 cm3.
908 cm3.
Le volume de la boîte est d'environ 908 cm3.
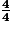
Vboîte 4/4 = Airebase × hauteur = πr2 × h = π ×
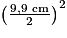 × 11,8 cm
× 11,8 cm  908 cm3.
908 cm3.Le volume de la boîte est d'environ 908 cm3.
2. Contenance affichée
Sachant que 1 L = 1 dm3, et que 1 dm3 = 1 000 cm3, alors on a l'équivalence 1 mL = 1 cm3.
D'après la question précédente, le volume total de la boîte est d'environ 908 mL.
Calculons 95 % de ce volume : 908 × 0,95 = 862,6 > 850.
Ainsi, si une boîte est remplie à 95 %, elle contient bien un peu plus que 850 mL.
Sachant que 1 L = 1 dm3, et que 1 dm3 = 1 000 cm3, alors on a l'équivalence 1 mL = 1 cm3.
D'après la question précédente, le volume total de la boîte est d'environ 908 mL.
Calculons 95 % de ce volume : 908 × 0,95 = 862,6 > 850.
Ainsi, si une boîte est remplie à 95 %, elle contient bien un peu plus que 850 mL.
3. Comparaison avec une boîte de diamètre double
• 1re méthode
En doublant le diamètre, on double le rayon.
L'aire de la base est donc multipliée par 22, soit par 4.
La hauteur restant la même, le volume de la nouvelle boîte est donc quadruplé, et non doublé.
L'affirmation est fausse.
En doublant le diamètre, on double le rayon.
L'aire de la base est donc multipliée par 22, soit par 4.
La hauteur restant la même, le volume de la nouvelle boîte est donc quadruplé, et non doublé.
L'affirmation est fausse.
• 2e méthode (en langue algébrique)
Notons r, d, h et V, respectivement le rayon, le diamètre, la hauteur et le volume de la boîte de départ.
Notons r', d', h' et V' respectivement le rayon, le diamètre, la hauteur et le volume de la nouvelle boîte.
On a : V = πr2 × h et V' = πr'2 × h'.
D'après les hypothèses :
Ainsi, le nouveau volume n'est pas doublé mais quadruplé.
Notons r, d, h et V, respectivement le rayon, le diamètre, la hauteur et le volume de la boîte de départ.
Notons r', d', h' et V' respectivement le rayon, le diamètre, la hauteur et le volume de la nouvelle boîte.
On a : V = πr2 × h et V' = πr'2 × h'.
D'après les hypothèses :
- d' = 2d (on double le diamètre), donc r' = 2r (on double le rayon) ;
- h' = h (la hauteur reste la même).
Ainsi, le nouveau volume n'est pas doublé mais quadruplé.
4. Volume d'une boîte de format 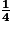
Vboîte 1/4 = Airebase × hauteur = πr2 × h = π ×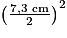 × 5,4 cm
× 5,4 cm  226 cm3.
226 cm3.
Or, 226 × 4 = 904, soit environ le volume de la boîte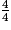 .
.
Ainsi, cette boîte a un volume quatre fois moindre que celui de la boîte de format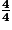 , ce qui justifie l'appellation de son format
, ce qui justifie l'appellation de son format 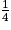 .
.
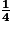
Vboîte 1/4 = Airebase × hauteur = πr2 × h = π ×
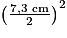 × 5,4 cm
× 5,4 cm  226 cm3.
226 cm3.Or, 226 × 4 = 904, soit environ le volume de la boîte
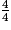 .
.Ainsi, cette boîte a un volume quatre fois moindre que celui de la boîte de format
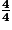 , ce qui justifie l'appellation de son format
, ce qui justifie l'appellation de son format 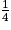 .
.B. Minimisation du coût de fabrication d'une boîte de conserve
1. Patron d'une boîte à main levée
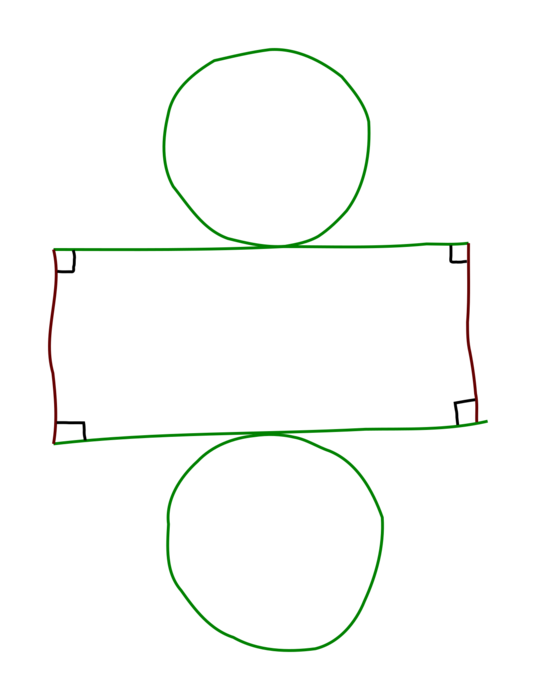 |
2. Hauteur en fonction du rayon
Si l'on appelle respectivement r, h et V, le rayon en cm, la hauteur en cm et le volume en cm3 de la boîte, alors nous avons l'égalité suivante : V = πr2h.
Donc : h =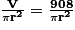 .
.
Si l'on appelle respectivement r, h et V, le rayon en cm, la hauteur en cm et le volume en cm3 de la boîte, alors nous avons l'égalité suivante : V = πr2h.
Donc : h =
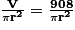 .
. 3. Le tableur
a) Formule pour calculer l'aire d'un disque de base
L'aire de la base étant égale à πr2, et la valeur du rayon étant donnée dans la cellule A2 (puis dans toute la colonne A), la formule adéquate est : =PI()*A2*A2, c'est-à-dire celle de la proposition 2.
L'aire de la base étant égale à πr2, et la valeur du rayon étant donnée dans la cellule A2 (puis dans toute la colonne A), la formule adéquate est : =PI()*A2*A2, c'est-à-dire celle de la proposition 2.
Remarque
On aurait pu proposer la formule =PI()*A2^2. b) Formule pour l'aire totale du cylindre
Le cylindre étant constitué d'un rectangle (la surface latérale) et de deux disques (les bases), la formule pour calculer l'aire totale s'écrit : =2*C2+D2.
Le cylindre étant constitué d'un rectangle (la surface latérale) et de deux disques (les bases), la formule pour calculer l'aire totale s'écrit : =2*C2+D2.
Remarque
On pouvait également donner la formule intégrale, sans tenir compte de la présence des colonnes C et D =2*PI()*A2^2+B2*2*PI()*A2. c) Encadrement du rayon pour un coût minimal
Le coût minimal correspond évidemment à une aire minimale de la surface fabriquée.
Dans le tableur, on peut constater une valeur minimale de l'aire de 520,3 pour un rayon de 5.
On ignore cependant si le minimum est atteint dans l'intervalle ]4 ; 5] ou dans l'intervalle [5 ; 6[.
On peut donc affirmer que l'aire minimale est obtenue pour un rayon compris entre 4 et 6 cm.
Le coût minimal correspond évidemment à une aire minimale de la surface fabriquée.
Dans le tableur, on peut constater une valeur minimale de l'aire de 520,3 pour un rayon de 5.
On ignore cependant si le minimum est atteint dans l'intervalle ]4 ; 5] ou dans l'intervalle [5 ; 6[.
On peut donc affirmer que l'aire minimale est obtenue pour un rayon compris entre 4 et 6 cm.
4. Représentation graphique de l'aire en fonction du rayon
a) L'aire et le rayon sont-ils proportionnels ?
L'aire n'est évidemment pas proportionnelle au rayon.
On peut invoquer plusieurs arguments, qui se suffisent tous à eux-mêmes :
L'aire n'est évidemment pas proportionnelle au rayon.
On peut invoquer plusieurs arguments, qui se suffisent tous à eux-mêmes :
- la courbe représentative n'est pas une droite ;
- la courbe ne passe pas par l'origine du repère ;
- la fonction change de variation : elle est décroissante puis croissante.
b) Aire totale pour un rayon de 4,24 cm
L'axe des abscisses est gradué tous les 2 dixièmes en graduation principale et tous les 4 centièmes en graduation secondaire.
En effet, un intervalle entre deux graduations principales est celui par exemple entre 4,2 et 4,4, donc il est bien de 2 dixièmes.
Les graduations principales sont subdivisées en 5 intervalles ; donc un intervalle entre deux graduations secondaires représente un cinquième de 2 dixièmes, soit 0,2 ÷ 5 = 0,04.
4,24 est donc représenté par la première graduation après 2,4.
La valeur lue est donc entre 541 et 542 cm2.
L'axe des abscisses est gradué tous les 2 dixièmes en graduation principale et tous les 4 centièmes en graduation secondaire.
En effet, un intervalle entre deux graduations principales est celui par exemple entre 4,2 et 4,4, donc il est bien de 2 dixièmes.
Les graduations principales sont subdivisées en 5 intervalles ; donc un intervalle entre deux graduations secondaires représente un cinquième de 2 dixièmes, soit 0,2 ÷ 5 = 0,04.
4,24 est donc représenté par la première graduation après 2,4.
La valeur lue est donc entre 541 et 542 cm2.
Remarque
L'énoncé demande une valeur et non un intervalle ; il est probable que toute valeur comprise entre 541 et 542 sera acceptée. L'important est toujours de préciser « environ » puisqu'une valeur lue ne peut être exacte, même si on a l'impression qu'elle se situe sur un trait de graduation. c) Rayons pour une aire totale de 530 cm2
On peut lire les deux valeurs suivantes :
On peut lire les deux valeurs suivantes :
- environ 4,52 cm (troisième graduation après 4,4) ;
- environ 6,04 cm (première graduation après 6).
d) Aire totale minimale
On peut lire environ 519 cm2.
On peut lire environ 519 cm2.
e) Rayon correspondant à l'aire totale minimale
Il est difficile de donner une valeur du rayon, on peut donner un intervalle plus précis que celui donné dans la question B.3.c), soit un rayon compris entre 5,2 et 5,28 cm.
Il est difficile de donner une valeur du rayon, on peut donner un intervalle plus précis que celui donné dans la question B.3.c), soit un rayon compris entre 5,2 et 5,28 cm.
Remarque
Comme précédemment, il est probable que toute valeur comprise entre 5,2 et 5,28 sera acceptée. f) Hauteur correspondant à l'aire totale minimale
Pour calculer cette hauteur, il faut choisir une valeur pour le rayon. Prenons par exemple la valeur médiane, soit r 5,24 cm.
5,24 cm.
On reprend l'expression que l'on a déterminée à la question B.2. :
h =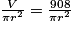 .
.
Soit, pour r = 5,24 cm, h =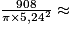 10,5.
10,5.
La hauteur correspondant à une aire totale minimale est donc d'environ 10,5 cm.
Pour calculer cette hauteur, il faut choisir une valeur pour le rayon. Prenons par exemple la valeur médiane, soit r
 5,24 cm.
5,24 cm.On reprend l'expression que l'on a déterminée à la question B.2. :
h =
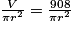 .
.Soit, pour r = 5,24 cm, h =
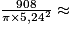 10,5.
10,5.La hauteur correspondant à une aire totale minimale est donc d'environ 10,5 cm.
Remarque
La valeur de la hauteur dépend bien sûr de la valeur du rayon choisi. Tout calcul compatible avec ce choix du rayon sera accepté. C. Livraison des boîtes
• Carton 1
Du point de vue de la masseLe carton contient 5 × 5 = 25 boîtes de 880 g chacune.
Soit une masse totale de : 25 × 880 g = 22 000 g = 22 kg.
Du point de vue des dimensions
Comme il n'y a qu'un seul étage, la hauteur du carton correspond peu ou prou à celle d'une boîte de format
 , soit 11,8 cm.
, soit 11,8 cm.La longueur et la largeur correspondent chacune à 5 diamètres, comme le montre le schéma ci-dessous, soit à 5 × 9,9 cm = 49,5 cm.
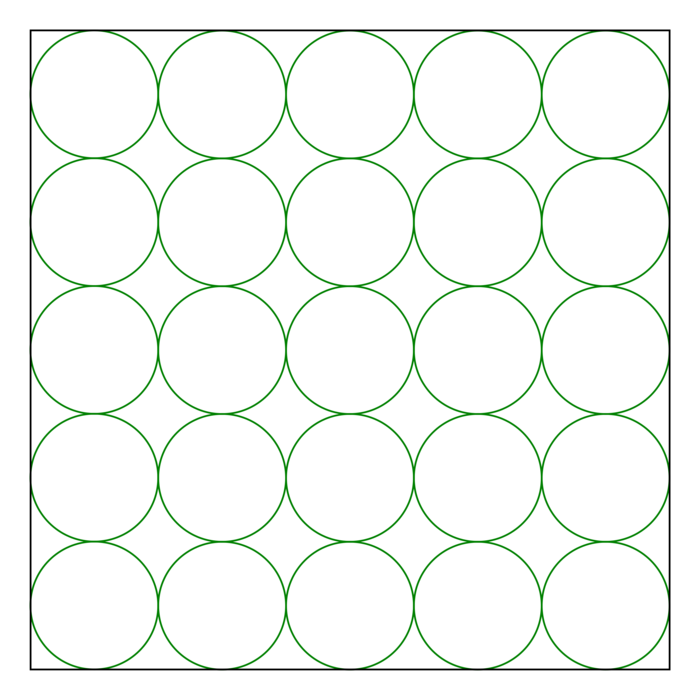 |
La somme totale des dimensions est donc :
11,8 cm + 2 × 49,5 cm = 110,8 cm > 100 cm.
Le carton 1 convient donc du point de vue de la masse, mais pas du point de vue des dimensions.
On ne peut donc pas choisir le carton 1.
11,8 cm + 2 × 49,5 cm = 110,8 cm > 100 cm.
Le carton 1 convient donc du point de vue de la masse, mais pas du point de vue des dimensions.
On ne peut donc pas choisir le carton 1.
• Carton 2
Du point de vue de la masseLe carton contient 3 × 4 × 2 = 24 boîtes de 880 g chacune.
Soit une masse totale de : 24 × 880 g = 21 120 g = 21,12 kg < 22 kg.
Du point de vue des dimensions
Comme il y a trois étages, la hauteur du carton correspond peu ou prou à celle de trois hauteurs d'une boîte de format
 , soit 3 × 11,8 cm = 35,4 cm.
, soit 3 × 11,8 cm = 35,4 cm.Comme le montre le schéma ci-dessous :
- la longueur correspond à 4 diamètres, soit à 4 × 9,9 cm = 39,6 cm ;
- la largeur correspond à 2 diamètres, soit à 2 × 9,9 cm = 19,8 cm.
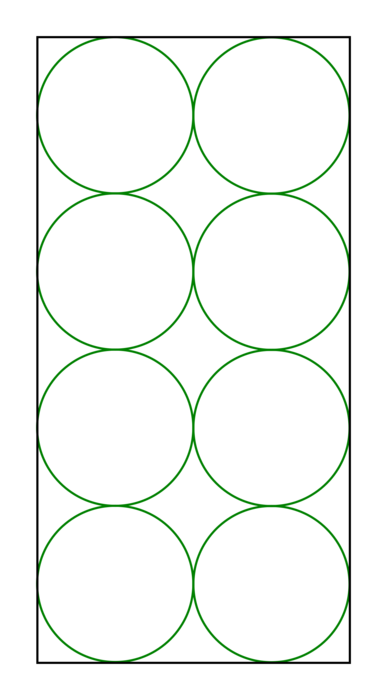 |
La somme totale des dimensions est donc :
35,4 cm + 39,6 cm + 19,8 cm = 94,8 cm < 100 cm.
Le carton 2 convient donc du point de vue de la masse et du point de vue des dimensions.
On peut donc choisir le carton 2.
35,4 cm + 39,6 cm + 19,8 cm = 94,8 cm < 100 cm.
Le carton 2 convient donc du point de vue de la masse et du point de vue des dimensions.
On peut donc choisir le carton 2.
• Carton 3
Du point de vue de la masseLe carton contient 3 × 3 × 3 = 27 boîtes de 880 g chacune
Soit une masse totale de : 27 × 880 g = 23 760 g = 23,76 kg > 22 kg.
Il est inutile d'aller plus loin, le carton 3 est trop lourd, peu importent ses dimensions.
On ne peut donc pas choisir le carton 3.
Deuxième partie
Exercice 1
1. Montrons que BC = 5,82 m
Le triangle ABC est rectangle en A, AB = 432 cm et AC = 390 cm.
D'après le théorème de Pythagore, on a donc : AB2 + AC2 = BC2.
D'où, les mesures de longueurs étant exprimées en cm : (4322 + 3902) cm2 = BC2.
Donc : BC =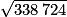 cm = 582 cm.
cm = 582 cm.
On en conclut que : BC = 582 cm = 5,82 m.
Le triangle ABC est rectangle en A, AB = 432 cm et AC = 390 cm.
D'après le théorème de Pythagore, on a donc : AB2 + AC2 = BC2.
D'où, les mesures de longueurs étant exprimées en cm : (4322 + 3902) cm2 = BC2.
Donc : BC =
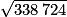 cm = 582 cm.
cm = 582 cm.On en conclut que : BC = 582 cm = 5,82 m.
2.
a) Calcul de la longueur AD
Les droites (AD) et (CE) sont sécantes en B et les droites (AC) et (DE) sont parallèles car toutes deux perpendiculaires à la droite (AB).
D'après le théorème de Thalès, on a donc :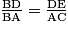 .
.
D'où :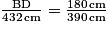 , et donc : BD =
, et donc : BD = 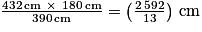 .
.
Comme D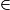 [AB], AD = AB − BD = 432 cm −
[AB], AD = AB − BD = 432 cm − 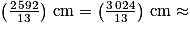 233 cm.
233 cm.
D se trouve à environ 233 cm, soit 2,33 m de A.
Les droites (AD) et (CE) sont sécantes en B et les droites (AC) et (DE) sont parallèles car toutes deux perpendiculaires à la droite (AB).
D'après le théorème de Thalès, on a donc :
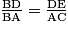 .
.D'où :
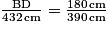 , et donc : BD =
, et donc : BD = 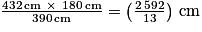 .
.Comme D
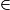 [AB], AD = AB − BD = 432 cm −
[AB], AD = AB − BD = 432 cm − 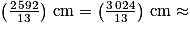 233 cm.
233 cm.D se trouve à environ 233 cm, soit 2,33 m de A.
b) Calcul de la superficie Carrez des combles
La surface correspondant à la superficie Carrez est un rectangle de largeur 2 × AD et de longueur BH.
La mesure de l'aire de ce rectangle, en m2, est donc : 2 × 2,33 × 20 93.
93.
La superficie Carrez des combles est d'environ 93 m2.
La surface correspondant à la superficie Carrez est un rectangle de largeur 2 × AD et de longueur BH.
La mesure de l'aire de ce rectangle, en m2, est donc : 2 × 2,33 × 20
 93.
93.La superficie Carrez des combles est d'environ 93 m2.
Exercice 2
1. Probabilité de gagner un lot
Il y a en tout : 1 + 5 + 10 + 14 + 30 + 100 = 160 lots gagnants.
4 000 tickets ont été vendus en tout. 160 ÷ 4 000 = 0,04.
La probabilité qu'Isabelle gagne est de 0,04.
Il y a en tout : 1 + 5 + 10 + 14 + 30 + 100 = 160 lots gagnants.
4 000 tickets ont été vendus en tout. 160 ÷ 4 000 = 0,04.
La probabilité qu'Isabelle gagne est de 0,04.
2. Probabilité de gagner une peluche
Il y a 100 peluches à gagner.
La probabilité de gagner une peluche est donc :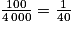 = 0,025.
= 0,025.
La probabilité de gagner une peluche est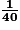 , soit 2,5 %.
, soit 2,5 %.
Il y a 100 peluches à gagner.
La probabilité de gagner une peluche est donc :
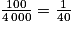 = 0,025.
= 0,025.La probabilité de gagner une peluche est
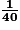 , soit 2,5 %.
, soit 2,5 %.3. Probabilité de gagner un lot d'une valeur d'au moins 100 €
Les lots d'une valeur supérieure ou égale à 100 € sont le téléviseur, les lecteurs Blu-ray et les smartphones. Le nombre de lots concernés est donc : 1 + 5 + 10 = 16.
La probabilité de gagner un lot d'une valeur supérieure ou égale à 100 € est donc :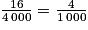 = 0,004.
= 0,004.
Les lots d'une valeur supérieure ou égale à 100 € sont le téléviseur, les lecteurs Blu-ray et les smartphones. Le nombre de lots concernés est donc : 1 + 5 + 10 = 16.
La probabilité de gagner un lot d'une valeur supérieure ou égale à 100 € est donc :
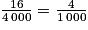 = 0,004.
= 0,004.4. Valeur moyenne d'un lot
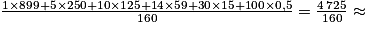 29,53.
29,53.
La valeur moyenne d'un lot est 29,53 €.
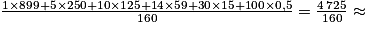 29,53.
29,53.La valeur moyenne d'un lot est 29,53 €.
5. Rapport de la tombola
On a vu à la question précédente que l'ensemble des lots vaut 4 725 €.
La vente des billets a rapporté : 4 000 × 2 € = 8 000 €.
8 000 € − 4 725 € = 3 275 €.
La tombola a rapporté 3 275 €.
On a vu à la question précédente que l'ensemble des lots vaut 4 725 €.
La vente des billets a rapporté : 4 000 × 2 € = 8 000 €.
8 000 € − 4 725 € = 3 275 €.
La tombola a rapporté 3 275 €.
6. Probabilité qu'une personne ayant acheté un ticket gagne un lot publicitaire
Remarque
Attention, il est question ici de la probabilité de gagner un lot publicitaire pour quiconque a acheté un ticket et non pas de la probabilité parmi ceux qui ont un ticket perdant (elle serait de 1/3).Cette question met en jeu la notion de probabilité conditionnelle, ici la probabilité d'obtenir un lot publicitaire, sachant que l'on a perdu à la loterie. Cette notion n'est pas au programme du cycle 4.
• 1re méthode : Raisonnement utilisant les probabilités conditionnelles
Pour gagner un lot publicitaire, il faut avoir acheté un ticket, avoir un ticket perdant, puis tirer la bonne carte parmi trois.La probabilité d'avoir acheté un ticket perdant est de : 1 − 0,04 = 0,96 puisque « acheter un ticket perdant » est l'événement contraire de « acheter un ticket gagnant », dont on a calculé la probabilité en 1.
Une fois que l'on a un ticket perdant, la probabilité de gagner un lot publicitaire est de : 1/3.
Pour quiconque achète un ticket, la probabilité d'obtenir un lot publicitaire est donc : 0,96 × 1/3 = 0,32 (soit 32 %).
• 2e méthode : Raisonnement sur les issues possibles
Sur les 4 000 tickets, il y a 4 000 − 160 = 3 840 tickets perdants.Il est équivalent à la deuxième loterie d'imaginer que, sur ces 3 840 tickets perdants, un tiers d'entre eux soit marqué pour obtenir un lot publicitaire, soit 3 840 ÷ 3 = 1 280 tickets.
Ainsi, sur les 4 000 tickets de départ, 1 280 tickets permettraient d'obtenir un lot publicitaire, soit une probabilité de
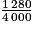 = 0,32.
= 0,32.Exercice 3
1. Résultat du programme A si on entre 10
Si on entre 10 dans le programme A, on obtient successivement :
10 − 4 = 6
6 × 6 = 36
36 − 16 = 20.
Le résultat est 20.
Si on entre 10 dans le programme A, on obtient successivement :
10 − 4 = 6
6 × 6 = 36
36 − 16 = 20.
Le résultat est 20.
2. Résultat du programme B si on entre 5,2
Si on entre 5,2 dans le programme B, on obtient successivement :
5,2 − 4 = 1,2
1,2 × 2 × 5,2 = 12,48.
Le résultat est 12,48.
Si on entre 5,2 dans le programme B, on obtient successivement :
5,2 − 4 = 1,2
1,2 × 2 × 5,2 = 12,48.
Le résultat est 12,48.
3. Nombre à entrer pour obtenir des résultats identiques pour A et B
Soit x le nombre entré dans le programme A.
Le programme calcule : (x − 4) × (x − 4) − 16 = x2 − 8x.
Soit x le nombre entré dans le programme B.
Le programme calcule : (x − 4) × 2x = 2x2 − 8x.
On obtient le même résultat pour les deux programmes si :
x2 − 8x = 2x2 − 8x.
On ajoute 8x aux deux membres de l'égalité : x2 = 2x2.
On enlève x2 aux deux membres de l'égalité : 0 = x2.
D'où : x2 = 0, soit x = 0.
On obtient des résultats identiques pour A et B si on entre « 0 » dans ces programmes.
Soit x le nombre entré dans le programme A.
Le programme calcule : (x − 4) × (x − 4) − 16 = x2 − 8x.
Soit x le nombre entré dans le programme B.
Le programme calcule : (x − 4) × 2x = 2x2 − 8x.
On obtient le même résultat pour les deux programmes si :
x2 − 8x = 2x2 − 8x.
On ajoute 8x aux deux membres de l'égalité : x2 = 2x2.
On enlève x2 aux deux membres de l'égalité : 0 = x2.
D'où : x2 = 0, soit x = 0.
On obtient des résultats identiques pour A et B si on entre « 0 » dans ces programmes.
4. Nombre à entrer en A pour obtenir 0
Soit x le nombre entré dans le programme A. Le programme calcule x2 − 8x.
On veut donc : x2 − 8x = 0, soit x(x − 8) = 0.
Un produit est nul si et seulement si l'un de ses facteurs est nul, d'où : x = 0 ou x = 8.
Pour obtenir 0, il faut entrer 0 ou 8 dans le programme A.
Soit x le nombre entré dans le programme A. Le programme calcule x2 − 8x.
On veut donc : x2 − 8x = 0, soit x(x − 8) = 0.
Un produit est nul si et seulement si l'un de ses facteurs est nul, d'où : x = 0 ou x = 8.
Pour obtenir 0, il faut entrer 0 ou 8 dans le programme A.
Troisième partie
Situation 1
1. Analyse des réponses erronées
La réponse a) correspond au calcul 13,25 ÷ 10 ; il est probable que l'élève a appliqué une règle de déplacement de la virgule de 1 rang, en se trompant de direction ; il ne met donc pas de sens derrière cette règle.
La réponse b) est le résultat probable de la règle valable pour les entiers : multiplier un nombre par 10 a pour effet d'ajouter un chiffre 0 à droite de son écriture. Ici, l'élève, associant bien cette règle aux nombres entiers, a « ajouté » le 0 à droite de la partie entière.
La réponse c) est le résultat probable de cette même règle, cette fois-ci appliquée à l'écriture globale.
La réponse d) est correcte, sans que l'on sache quelle est la procédure de l'élève.
La réponse a) correspond au calcul 13,25 ÷ 10 ; il est probable que l'élève a appliqué une règle de déplacement de la virgule de 1 rang, en se trompant de direction ; il ne met donc pas de sens derrière cette règle.
La réponse b) est le résultat probable de la règle valable pour les entiers : multiplier un nombre par 10 a pour effet d'ajouter un chiffre 0 à droite de son écriture. Ici, l'élève, associant bien cette règle aux nombres entiers, a « ajouté » le 0 à droite de la partie entière.
La réponse c) est le résultat probable de cette même règle, cette fois-ci appliquée à l'écriture globale.
La réponse d) est correcte, sans que l'on sache quelle est la procédure de l'élève.
2. Trace écrite de la multiplication par 10
a) Critique des deux propositions
• Proposition a : « Pour multiplier par 10, on ajoute un zéro à droite du nombre. »
- Critique n° 1 : un nombre n'a ni droite, ni gauche, on ne peut donc pas dire « à la droite du nombre » ;
- Critique n° 2 : ce n'est pas au nombre que l'on « ajoute un zéro », mais à son écriture décimale, à laquelle on ajoute le chiffre zéro.
- Critique n° 3 : cette règle, énoncée correctement, ne fonctionne que pour les nombres entiers ; on ne peut donc pas l'étendre aux nombres décimaux non entiers, encore moins aux nombres irrationnels.
Remarque
Ainsi, s'il fallait vraiment l'énoncer, il faudrait privilégier une formulation telle que :« Multiplier un nombre entier par 10 a pour effet d'ajouter un chiffre zéro à la droite de son écriture décimale ».
Mais, et c'est l'objet de la critique n° 4, faut-il l'énoncer ?
- Critique n° 4 : cette règle est purement technique, et non porteuse de sens ; elle peut être pratique pour aller plus vite une fois que l'on a compris le mécanisme, mais ne peut participer à la construction du sens de la multiplication par 10.
Remarque
Il est probable que la critique n° 3 était celle attendue.• Proposition b : « Pour multiplier par 10, on déplace la virgule vers la droite. »
- Critique n° 1 : Toutes les écritures des nombres n'ont pas de virgule, donc elle ne convient pas à tous les nombres. Par exemple, pour multiplier 34 par 10, on ne déplace aucune virgule.
- Critique n° 2 : Elle est incomplète pour les nombres dont les écritures possèdent une virgule. Par exemple, pour multiplier 0,4 par 10, non seulement la virgule « se déplace », met elle disparaît, ainsi que le chiffre zéro.
- Critique n° 3 : Comme la précédente, cette proposition n'est pas porteuse de sens, et ne peut être efficace qu'une fois que l'on a compris. Elle est même contraire à ce qui se passe en réalité, à savoir que ce sont les chiffres qui « se déplacent » (en fait, qui changent d'unité de numération), et non la virgule.
b) Institutionnalisation de la multiplication par 10
Lorsque l'on multiplie un nombre décimal par 10, chacune des unités de numération qui le compose devient 10 fois plus grande ; chacun des chiffres de son écriture décimale s'exprime donc dans une unité de numération 10 fois plus grande, et se décale donc d'une unité vers la gauche (vers l'agrandissement des unités de numération).
Lorsque l'on multiplie un nombre décimal par 10, chacune des unités de numération qui le compose devient 10 fois plus grande ; chacun des chiffres de son écriture décimale s'exprime donc dans une unité de numération 10 fois plus grande, et se décale donc d'une unité vers la gauche (vers l'agrandissement des unités de numération).
Remarque
Cette institutionnalisation est purement théorique et n'est là que pour prouver que vous (futur(e) enseignant(e)) savez décrire la technologie. Pour des élèves, il est beaucoup plus judicieux de fonctionner sur des exemples.
Institutionnalisation extraite de l'annexe 4 du document ressource « fractions et décimaux au cycle 3 ».
« Multiplier par 10, c'est donner à chaque chiffre une valeur 10 fois plus grande, le chiffre des unités devient donc le chiffre des dizaines, le chiffre des dixièmes devient celui des unités, etc.
12,37, c'est 12 unités, 3 dixièmes et 7 centièmes.
12,37 × 10, c'est donc 12 dizaines, 3 unités et 7 dixièmes, donc 123,7. »
3. Utilisation du glisse-nombre
• Pour l'élève ayant répondu « a) 1,325 »
Il n'est pas dit que le glisse-nombre puisse l'aider puisque cette écriture s'obtient bien en tirant la languette vers la droite.
On peut toujours enseigner que « tirer, c'est diviser » et « pousser, c'est multiplier », mais cela n'est pas plus porteur de sens que « vers la gauche » ou « vers la droite ».
Cela dit, l'usage du glisse-nombre peut tout de même lui faire comprendre que la position de la virgule reste fixe, et que ce sont les chiffres qui changent de position.
Il n'est pas dit que le glisse-nombre puisse l'aider puisque cette écriture s'obtient bien en tirant la languette vers la droite.
On peut toujours enseigner que « tirer, c'est diviser » et « pousser, c'est multiplier », mais cela n'est pas plus porteur de sens que « vers la gauche » ou « vers la droite ».
Cela dit, l'usage du glisse-nombre peut tout de même lui faire comprendre que la position de la virgule reste fixe, et que ce sont les chiffres qui changent de position.
• Pour l'élève ayant répondu « b) 130,25 »
Le glisse-nombre permet de visualiser que les chiffres restent dans la même position relative les uns par rapport aux autres, et que l'ajout d'un zéro en plein milieu n'est pas pertinent. Mais est-ce suffisant pour donner du sens ?
Le glisse-nombre permet de visualiser que les chiffres restent dans la même position relative les uns par rapport aux autres, et que l'ajout d'un zéro en plein milieu n'est pas pertinent. Mais est-ce suffisant pour donner du sens ?
• Pour l'élève ayant répondu « c) 13,250 »
Cet élève peut aussi bien ajouter un zéro sur le glisse-nombre et ne percevra pas son erreur sans intervention.
Cet élève peut aussi bien ajouter un zéro sur le glisse-nombre et ne percevra pas son erreur sans intervention.
Situation 2
Remarque
Analyse préalable du problème (à rapidement faire au brouillon) : il s'agit d'un problème arithmétique complexe. Les problèmes basiques sous-jacents nécessaires à extraire pour sa résolution sont :
- soit un problème de composition de trois états pour obtenir la somme due : 2,35 € + 1,15 € + 1,15 € = 4,65 € ;
- soit un problème de proportionnalité simple dans le sens de la multiplication (avec connaissance de la valeur unitaire) pour trouver le prix des viennoiseries : 2 × 1,15 € = 2,30 €, suivi d'un problème de composition de deux états pour trouver la somme due : 2,30 € + 2,35 € = 4,65 € ;
- le tout suivi d'un problème de transformation négative avec recherche de l'état final pour obtenir le montant de la monnaie : 10 € − 4,65 € = 5,35 € (en reformulant ce dernier problème de la façon suivante : « Théo a 10 €. Il doit donner 4,65 € ; combien lui reste-t-il ? »).
1. Analyse des productions d'élèves au regard des compétences « modéliser » et « calculer »
• L'élève A ne dégage aucun des problèmes basiques sous-jacents au problème, l'opération qu'il effectue consiste à additionner les trois nombres de l'énoncé, sans que le résultat puisse être qualifié dans le contexte du problème. Il ne modélise donc pas le problème.
En revanche, son addition est correctement posée et effectuée, avec la retenue gérée mentalement. Cet élève montre donc clairement certaines compétences en calcul, plus précisément en addition posée.
En revanche, son addition est correctement posée et effectuée, avec la retenue gérée mentalement. Cet élève montre donc clairement certaines compétences en calcul, plus précisément en addition posée.
• L'élève B dégage correctement les deux problèmes basiques sous-jacents, celui permettant d'obtenir le coût total (première opération), et celui permettant d'obtenir la somme rendue (seconde opération). Il a donc correctement et entièrement modéliser le problème par une addition de trois termes, suivie d'une soustraction.
L'addition est correctement effectuée ; en revanche, la soustraction est faite « à l'envers » pour la partie décimale ; il ne sait pas effectuer une soustraction posée lorsque les « chiffres du bas » sont plus grands que ceux « du haut », et il ne contrôle pas son résultat à l'aide d'un calcul réfléchi. Du point de vue du calcul, il montre donc une compétence algorithmique en addition, mais pas en soustraction.
L'addition est correctement effectuée ; en revanche, la soustraction est faite « à l'envers » pour la partie décimale ; il ne sait pas effectuer une soustraction posée lorsque les « chiffres du bas » sont plus grands que ceux « du haut », et il ne contrôle pas son résultat à l'aide d'un calcul réfléchi. Du point de vue du calcul, il montre donc une compétence algorithmique en addition, mais pas en soustraction.
• Comme l'élève B, l'élève C dégage correctement les problèmes sous-jacents ; il a décomposé le problème en trois problèmes basiques (l'un étant traité mentalement) au lieu de deux. Il a modélisé le problème par la succession d'une multiplication (ou une addition itérée de 1,15, on ne peut le savoir), d'une addition et d'une soustraction.
La première opération (multiplication par deux ou addition itérée) est effectuée mentalement, les deux autres sont posées sans erreur. Du point de vue du calcul, il est donc suffisamment outillé pour pouvoir choisir sa technique en fonction des nombres en jeu, et mener à bien ses calculs sans erreur.
La première opération (multiplication par deux ou addition itérée) est effectuée mentalement, les deux autres sont posées sans erreur. Du point de vue du calcul, il est donc suffisamment outillé pour pouvoir choisir sa technique en fonction des nombres en jeu, et mener à bien ses calculs sans erreur.
• L'élève D a correctement dégagé le second problème, celui du rendu de la monnaie, mais non le premier. Est-ce un problème de modélisation ou de simple lecture trop rapide de l'énoncé ?, on ne saurait le dire. La succession d'une addition pour trouver la somme totale, puis d'une soustraction pour trouver le reste montre une compétence réelle en modélisation, même si elle peut être encore instable.
Du point de vue du calcul, la première opération est une addition posée correctement, dont le résultat est correct. La seconde opération est écrite en ligne et effectuée mentalement, avec une erreur de raisonnement dans le calcul réfléchi. Cet élève montre donc une compétence incomplète en calcul : une technique correcte de l'algorithme de pose de l'addition, une confiance en lui suffisante pour choisir le type de calcul (il n'existe donc pas que le calcul posé dans la vie), mais une fragilité en calcul réfléchi, sans que l'on puisse dire laquelle avec aussi peu d'éléments.
Du point de vue du calcul, la première opération est une addition posée correctement, dont le résultat est correct. La seconde opération est écrite en ligne et effectuée mentalement, avec une erreur de raisonnement dans le calcul réfléchi. Cet élève montre donc une compétence incomplète en calcul : une technique correcte de l'algorithme de pose de l'addition, une confiance en lui suffisante pour choisir le type de calcul (il n'existe donc pas que le calcul posé dans la vie), mais une fragilité en calcul réfléchi, sans que l'on puisse dire laquelle avec aussi peu d'éléments.
2. Activités de remédiation pour l'élève A
La remédiation proposée doit permettre à l'élève de reconnaître les problèmes élémentaires sous-jacents, de connecter les données et de qualifier les résultats.
Considérons que l'expression « ce type de problème » recouvre à la fois la structure du problème et son contexte, une première activité de remédiation pouvant être proposée à l'élève, avec du matériel, est de « jouer au jeu de la marchande », avec de la monnaie factice et une situation d'achat évoquée proche du problème proposé. L'élève pourrait ainsi mettre en scène la situation, ce qui peut l'aider à connecter les données ; sa verbalisation de la situation jouée lui donnant l'occasion de qualifier les résultats.
Une activité de remédiation sans matériel spécifique pourrait consister en une demande explicite à l'élève de représenter la situation de telle sorte que toutes les informations utiles soient présentes sur la représentation. Une exploitation de la production de l'élève (dessin ou schéma) centrée sur la présence – ou non – des données numériques utiles, mais aussi des relations entre ces données permettra de (re)travailler connexion et qualification des données ou résultats.
La remédiation proposée doit permettre à l'élève de reconnaître les problèmes élémentaires sous-jacents, de connecter les données et de qualifier les résultats.
Considérons que l'expression « ce type de problème » recouvre à la fois la structure du problème et son contexte, une première activité de remédiation pouvant être proposée à l'élève, avec du matériel, est de « jouer au jeu de la marchande », avec de la monnaie factice et une situation d'achat évoquée proche du problème proposé. L'élève pourrait ainsi mettre en scène la situation, ce qui peut l'aider à connecter les données ; sa verbalisation de la situation jouée lui donnant l'occasion de qualifier les résultats.
Une activité de remédiation sans matériel spécifique pourrait consister en une demande explicite à l'élève de représenter la situation de telle sorte que toutes les informations utiles soient présentes sur la représentation. Une exploitation de la production de l'élève (dessin ou schéma) centrée sur la présence – ou non – des données numériques utiles, mais aussi des relations entre ces données permettra de (re)travailler connexion et qualification des données ou résultats.
3. Proposition de l'enseignant pour que l'élève B puisse repérer son erreur
L'élève B a fait une erreur de calcul dans sa soustraction posée.
L'enseignant peut lui rappeler que l'on peut vérifier le calcul d'une différence en effectuant la somme « différence calculée plus terme retranché », en faisant le lien entre différence et addition à trou. Ainsi, ici, si l'élève opère 6,65 + 4,65, il se rendra compte qu'il n'obtient pas 10.
L'élève B a fait une erreur de calcul dans sa soustraction posée.
L'enseignant peut lui rappeler que l'on peut vérifier le calcul d'une différence en effectuant la somme « différence calculée plus terme retranché », en faisant le lien entre différence et addition à trou. Ainsi, ici, si l'élève opère 6,65 + 4,65, il se rendra compte qu'il n'obtient pas 10.
4. Difficulté ne pouvant être détectée par l'enseignant lorsqu'il propose le deuxième problème
Le deuxième problème est un problème élémentaire (cf. Houdement), qui correspond à la dernière étape du problème initial. L'enseignant ne pourra donc pas détecter la difficulté que peuvent avoir certains élèves à percevoir les problèmes sous-jacents à un problème complexe.
Le deuxième problème est un problème élémentaire (cf. Houdement), qui correspond à la dernière étape du problème initial. L'enseignant ne pourra donc pas détecter la difficulté que peuvent avoir certains élèves à percevoir les problèmes sous-jacents à un problème complexe.
Situation 3
1. Intérêt et limite de la situation
• Intérêt : La situation permet de (re)travailler la perception des positions relatives et le vocabulaire des repères spatiaux (devant, derrière, sur, sous, entre) qui sont au programme du cycle 1.
Remarque
Il ne peut que s'agir d'une situation de réinvestissement. • Limite : Les positions relatives doivent être reconnues sur une représentation plane d'un espace physique en 3D, ce qui pose le problème du passage d'une représentation plane à l'espace. Par ailleurs, les élèves n'ont aucun moyen de validation avec le matériel à disposition.
2. Analyse des réponses données aux affirmations C et E
Affirmation C : La réponse attendue est la réponse 3, que donnent des élèves. Les élèves qui répondent 6 ou 8 connaissent le sens du marqueur spatial « sur », mais ne distinguent pas « un cube » de « un pont de cubes » ou de « une tour de cubes ».
Affirmation E : La réponse attendue est la réponse 2, qui est donnée. Les élèves qui répondent 6 savent ce qu'est un pont de cubes, mais ne distinguent pas ou confondent « sur » et « sous ».
Affirmation C : La réponse attendue est la réponse 3, que donnent des élèves. Les élèves qui répondent 6 ou 8 connaissent le sens du marqueur spatial « sur », mais ne distinguent pas « un cube » de « un pont de cubes » ou de « une tour de cubes ».
Affirmation E : La réponse attendue est la réponse 2, qui est donnée. Les élèves qui répondent 6 savent ce qu'est un pont de cubes, mais ne distinguent pas ou confondent « sur » et « sous ».
3. Conclusion au fait que tous les élèves ont réussi à donner l'image correspondant à l'assertion B
On peut en conclure que les élèves savent reconnaître la seule image sur laquelle se trouve la princesse, et donc qu'ils savent distinguer la princesse du koala.
On peut en conclure que les élèves savent reconnaître la seule image sur laquelle se trouve la princesse, et donc qu'ils savent distinguer la princesse du koala.
4. Justification du choix de l'enseignant
En mettant le matériel représenté à disposition de l'élève, l'enseignant lui permet de reproduire les positions relatives des objets représentés et de les observer, ce qui ne permettra pas forcément à l'élève de remettre sa réponse en question, sans un étayage langagier de l'enseignant. En effet, il faudra, en accompagnement, reverbaliser ou faire reverbaliser ce que signifie « être devant la tour » s'agissant d'un objet (la tour) non intrinsèquement orienté : « devant » est relatif au spectateur (et non au koala, comme le pense l'élève).
En mettant le matériel représenté à disposition de l'élève, l'enseignant lui permet de reproduire les positions relatives des objets représentés et de les observer, ce qui ne permettra pas forcément à l'élève de remettre sa réponse en question, sans un étayage langagier de l'enseignant. En effet, il faudra, en accompagnement, reverbaliser ou faire reverbaliser ce que signifie « être devant la tour » s'agissant d'un objet (la tour) non intrinsèquement orienté : « devant » est relatif au spectateur (et non au koala, comme le pense l'élève).
Document suivant
Sujet 2020, groupement académique 2
