un partenariat
Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
Le propriétaire d'une maison décide de créer un appentis pour stocker du bois de chauffage. Un schéma de ce qu'il souhaite réaliser est donné ci-dessous.
 |
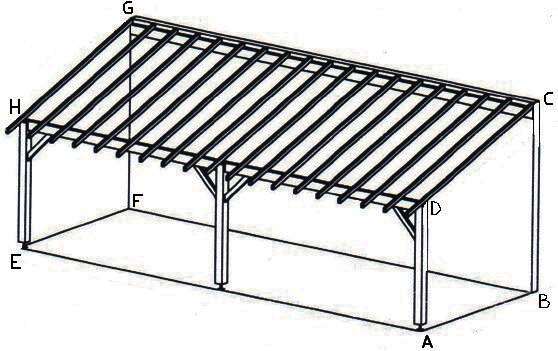Le rectangle ABFE représente une dalle de béton.
Le quadrilatère ABCD est un trapèze rectangle.
Le quadrilatère ABCD est un trapèze rectangle.
Les contraintes de sa maison et de son terrain lui imposent les dimensions suivantes :
AE = 4,8 m, AB = 1,5 m, AD = 2,4 m et BC = 3,2 m.
AE = 4,8 m, AB = 1,5 m, AD = 2,4 m et BC = 3,2 m.
Le volume utile de cet appentis est la partie dans laquelle il pourra stocker son bois sachant que, pour rester au sec, il devra se trouver sur la dalle de béton et sous le toit.
Le volume utile représente donc un prisme droit dont la base est le trapèze rectangle ABCD.
Le volume utile représente donc un prisme droit dont la base est le trapèze rectangle ABCD.
A. Surface de l'appentis et étude du volume utile
1. Dans le cadre de sa déclaration préalable de travaux, le propriétaire doit déterminer la surface au sol de l'appentis. Calculer l'aire du rectangle ABFE.
2.
a) On appelle I le point du segment [BC] tel que ABID est un rectangle. Calculer la longueur CD.
b) En déduire la surface du toit CDHG.
c) Calculer l'angle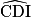 
, correspondant à la pente du toit. Arrondir la réponse au degré.
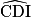, correspondant à la pente du toit. Arrondir la réponse au degré.3.
a) Construire A'B'C'D' une représentation du quadrilatère ABCD à l'échelle 1/50 en précisant les calculs qui ont permis cette construction.
b) Calculer l'aire du trapèze ABCD.
c) Pour être sûr de passer l'hiver au chaud, le propriétaire doit disposer de 15 stères de bois. Le stère est une unité de mesure, utilisée pour le bois de chauffage, valant 1 m3. Aura-t-il assez de place pour stocker ces 15 stères de bois ?
B. Réalisation de la dalle
Pour réaliser la dalle en béton, on creuse la terre au niveau du rectangle ABFE sur une profondeur de 25 cm.
1. Lorsqu'on extrait de la terre du sol, son volume augmente de 30 % du fait qu'elle n'est plus tassée.
Pour évacuer cette terre, le propriétaire utilise sa propre remorque qui contient au maximum 0,7 m3.
Combien de voyages sont-ils nécessaires pour évacuer complètement la terre ?
Pour évacuer cette terre, le propriétaire utilise sa propre remorque qui contient au maximum 0,7 m3.
Combien de voyages sont-ils nécessaires pour évacuer complètement la terre ?
2. Le propriétaire souhaite faire réaliser la dalle par un entrepreneur. Le trou creusé sera entièrement rempli de béton jusqu'au niveau du sol.
Le prix de la réalisation comporte la livraison par camion toupie et le prix du béton. Le propriétaire consulte deux entrepreneurs :
Le prix de la réalisation comporte la livraison par camion toupie et le prix du béton. Le propriétaire consulte deux entrepreneurs :
- L'entrepreneur A propose un tarif de 98 euros le mètre cube avec une livraison coûtant 150 euros par camion toupie, un camion toupie pouvant contenir 7 m3.
- L'entrepreneur B propose un tarif de 75 euros le mètre cube avec une livraison coûtant 240 euros par camion toupie, un camion toupie pouvant contenir 10 m3.
a) Calculer le prix facturé pour l'achat de 8 m3 de béton livrés par chacun des entrepreneurs.
b) On appelle f la fonction qui, au volume de béton x, exprimé en m3, associe f(x) le coût en euros proposé par l'entrepreneur A et g la fonction qui, au volume de béton x, exprimé en m3, associe g(x) le coût en euros proposé par l'entrepreneur B.
Le graphique ci-dessous donne les représentations graphiques des deux fonctions f et g pour x compris entre 0 et 5,5.
Le graphique ci-dessous donne les représentations graphiques des deux fonctions f et g pour x compris entre 0 et 5,5.
 |
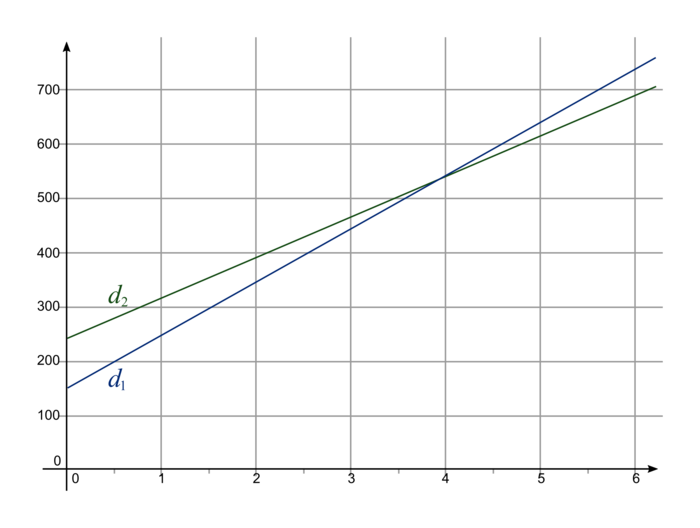Préciser, en justifiant la réponse, de quelle fonction f ou g, les droites d1 et d2 sont les représentations graphiques.
c) Par lecture graphique, déterminer une valeur approchée du volume maximum de béton que l'on peut commander avec la somme de 600 euros.
d) Déterminer graphiquement l'entrepreneur que le propriétaire doit choisir pour obtenir un prix de commande minimum pour réaliser la dalle de l'appentis. Calculer ensuite le prix qu'il devra alors payer.
e) Déterminer, par le calcul, une valeur approchée, au dixième près de mètre cube, du volume de béton à partir duquel il est préférable de changer d'entrepreneur pour une commande comprise entre 0 et 7 m3.
Deuxième partie (13 points)
Cette partie est composée de quatre exercices indépendants.
Exercice 1
Le programme ci-dessous a été écrit avec le logiciel Scratch pour tracer une figure. Il utilise une variable appelée « longueur ». L'unité de longueur est le pixel.
 |
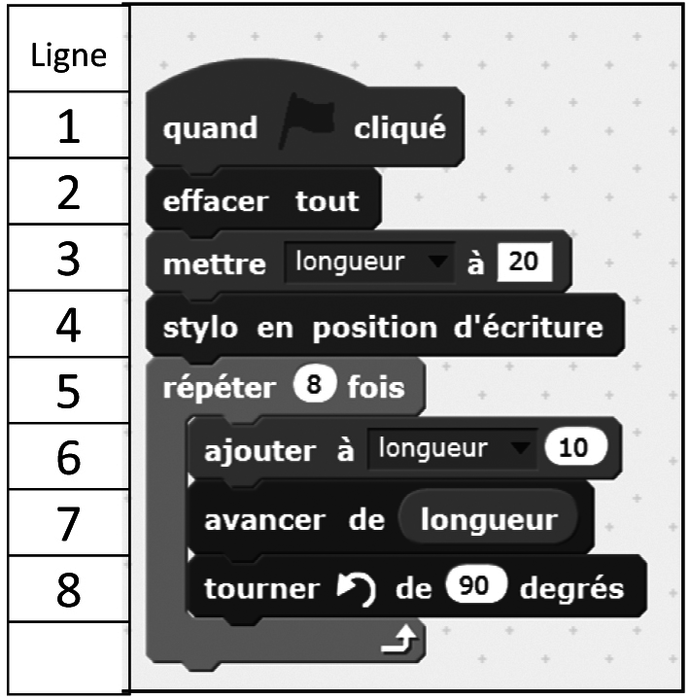On suppose que le premier tracé se fait horizontalement vers la droite.
1. Construire sur la copie la figure obtenue en lançant le programme, en prenant 1 cm pour 10 pixels.
2. Quelle figure obtient-on si on supprime la ligne 6 du programme ?
3. Que doit-on modifier dans le programme précédent pour construire un octogone régulier ayant des côtés de longueur 40 pixels ?
On rappelle qu'un polygone régulier est un polygone convexe dont tous les côtés ont la même longueur et tous les angles ont la même mesure.
On rappelle qu'un polygone régulier est un polygone convexe dont tous les côtés ont la même longueur et tous les angles ont la même mesure.
Exercice 2
Répondre aux quatre questions suivantes en utilisant les trois documents ci-après.
1. Un véhicule a parcouru le tronçon du tunnel de Noailles et la vitesse moyenne calculée est de 123 km/h. Quelle sera la vitesse retenue ?
2. Un autre véhicule a parcouru la distance entre les deux points d'enregistrement en 4 minutes. Quelle sera la vitesse retenue ?
3. Sur une contravention reçue suite à un excès de vitesse sur ce tronçon, la vitesse retenue est 114 km/h. Quelle était la vitesse moyenne calculée par l'ordinateur pour ce véhicule ?
4. La plaque d'immatriculation d'un véhicule est enregistrée à 9 h 17 min 56 s devant le premier radar, puis à 9 h 22 min 07 s devant le second radar. Le conducteur de ce véhicule sera-t-il sanctionné par une contravention ?
Document 1 : Le radar tronçon du tunnel de Noailles
| La portion de l'autoroute A20 entre Toulouse et Paris est équipée d'un radar-tronçon sur une distance de 5,1 km à proximité du tunnel de Noailles. La vitesse est limitée à 70 km/h lors de travaux de réfection du tunnel. |
Document 2 : Principe de fonctionnement d'un radar-tronçon
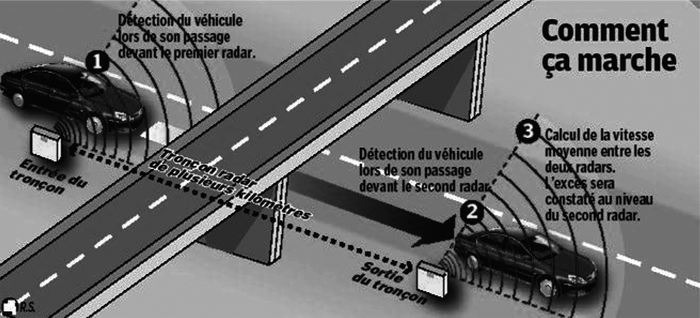 Source : www.leparisien.fr |
Document 3 : Calcul de la vitesse retenue pour la contravention
| Un ordinateur calcule la vitesse moyenne de la voiture sur le tronçon puis détermine la vitesse retenue afin de prendre en compte les erreurs de précision du radar. Si la vitesse retenue est au-dessus de la vitesse limite, l'automobiliste reçoit une contravention. |
| Vitesse moyenne calculée par l'ordinateur | inférieure ou égale à 100 km/h | supérieure à 100 km/h |
|---|---|---|
| Vitesse retenue | On enlève 5 km/h à la vitesse moyenne calculée. | On diminue la vitesse moyenne calculée de 5 %. |
Exercice 3
On dispose de plusieurs cubes pleins (non creux) de 5 cm d'arête. Certains sont en fer, les autres sont en nickel. La masse volumique du fer est de 7 860 kg/m3, celle du nickel est de 8 900 kg/m3.
On choisit un cube, on le pèse et on trouve que sa masse est 1 110 g.
Ce cube est-il en fer ou en nickel ?
On choisit un cube, on le pèse et on trouve que sa masse est 1 110 g.
Ce cube est-il en fer ou en nickel ?
Exercice 4
La répartition de l'âge des membres d'un club d'aviron est donnée par le graphique ci-dessous.
 |
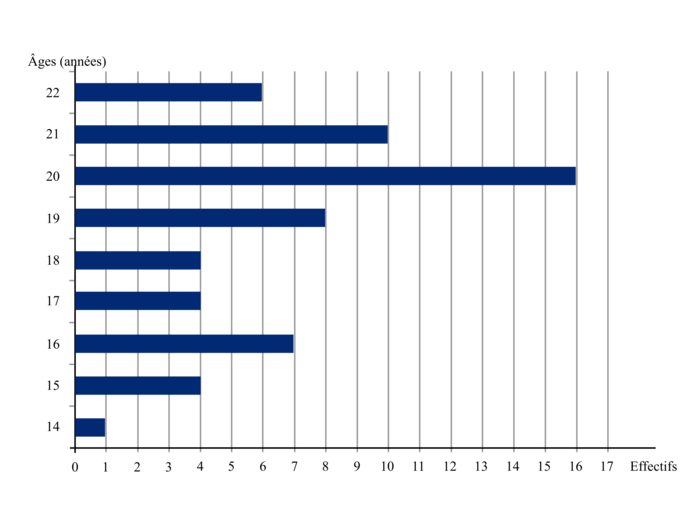1. Déterminer l'âge médian des membres du club. Justifier la réponse.
2. Quel est le pourcentage, arrondi à l'unité, de membres du club qui ont moins de 18 ans ?
3. Une tombola est organisée pour tous les membres du club. Chaque membre a reçu un billet au hasard. Le tirage au sort pour cette tombola désigne un seul gagnant.
Les probabilités trouvées seront arrondies au centième.
Les probabilités trouvées seront arrondies au centième.
a) Quelle est la probabilité pour que le gagnant ait 22 ans ?
b) Quelle est la probabilité pour que le gagnant ait au moins 18 ans ?
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Dans une classe de CM2, un enseignant commence une séquence d'apprentissage par le problème suivant :
| Il faut 6 oranges pour obtenir 300 mL de jus d'orange. On admet que toutes les oranges fournissent la même quantité de jus. Quelle quantité de jus peut-on obtenir avec 9 oranges ? |
1. De quelle notion mathématique relève ce problème ? Justifier la réponse.
2. Citer trois procédures que l'on peut attendre d'élèves de CM2 pour résoudre ce problème.
3. Modifier les données numériques de l'énoncé du problème afin d'amener les élèves à utiliser la procédure dite de « passage par l'unité ».
Situation 2
Dans le cadre d'une séquence ayant pour objectif de calculer avec des multiples de 25, l'enseignant d'une classe de CE2 donne l'exercice ci-dessous.
| Le compte est bon : il s'agit de trouver le nombre en gras, ou à défaut un nombre le plus proche possible, en utilisant les nombres situés en dessous. Chacun d'entre eux ne peut être utilisé qu'une fois. Il est possible d'utiliser les quatre opérations. 98 25 – 10 – 4 – 75 – 50 – 8 |
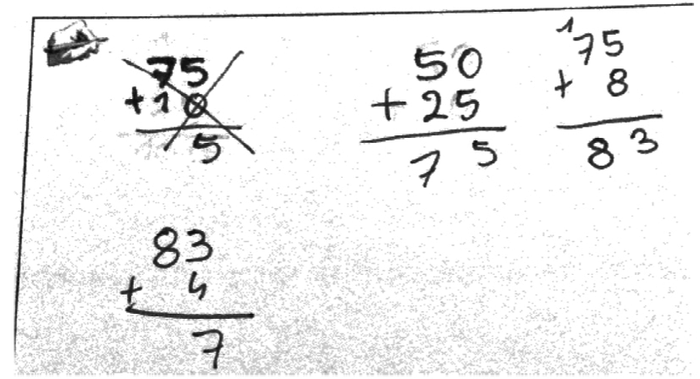
1. Ci-dessous sont présentées les productions de quatre élèves. Analyser chaque production A, B, C et D en termes de réussites et d'éventuelles erreurs.
 |
 |
 |
 |
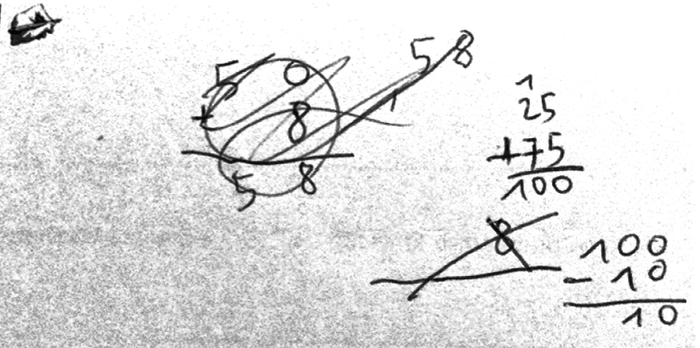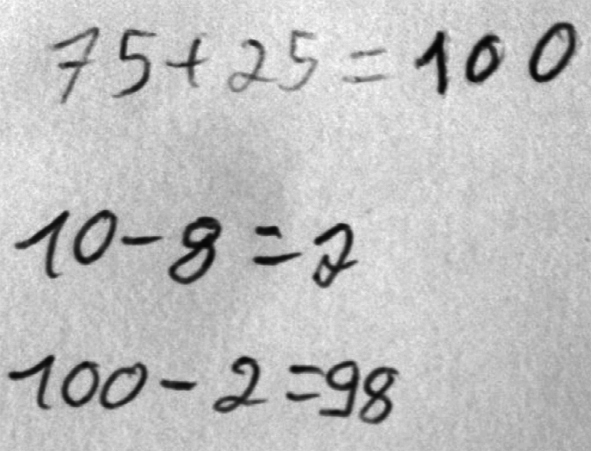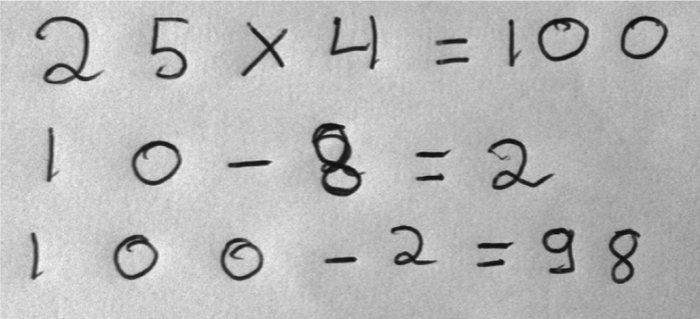2. Quels sont les faits numériques, liés à l'objectif de l'enseignant, connus des élèves C et D ?
3. Proposer un nouvel exercice de « compte est bon » ayant pour objectif de réinvestir la connaissance des multiples de 9 et deux solutions attendues des élèves.
4. Citer deux avantages de l'activité « Le compte est bon » dans l'apprentissage du calcul mental et deux points de vigilance que doit avoir un enseignant qui propose une activité « Le compte est bon ».
Situation 3
Lors d'une séance de calcul en ligne, une enseignante de CM2 propose le calcul suivant :
12,47 + 2,7
12,47 + 2,7
Voici les productions de quatre élèves :
 |
 |
 |
 |
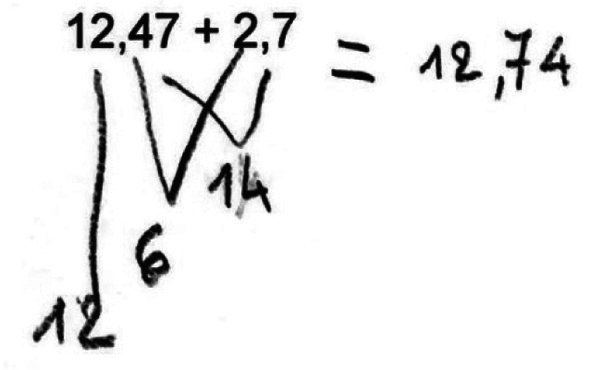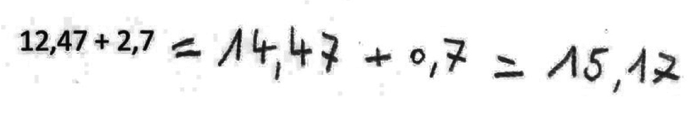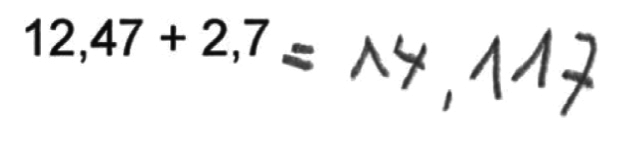1. En quoi le calcul en ligne est-il un mode de calcul complémentaire au calcul mental ?
2. Pour chacun des élèves, expliciter les procédures utilisées et analyser les erreurs éventuelles.
3. Quel étayage l'enseignante pourrait-elle proposer à Zoé pour l'aider à corriger l'erreur qu'elle a faite ?
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Surface de l'appentis et étude du volume utile
1. Aire du rectangle ABFE
AABFE = AE × AB = 1,5 m × 4,8 m = 7,2 m2.
L'aire du rectangle ABFE est 7,2 m2.
AABFE = AE × AB = 1,5 m × 4,8 m = 7,2 m2.
L'aire du rectangle ABFE est 7,2 m2.
2.
a) Longueur CD
Le triangle DIC est rectangle en I. Comme I est sur [BC], BI + IC = BC.
D'où : IC = BC − BI = 3,2 m − 2,4 m = 0,8 m.
Par ailleurs, ID = AB = 1,5 m.
D'après le théorème de Pythagore, on a : ID2 + IC2 = DC2.
D'où : DC =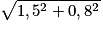
m = 1,7 m.
La longueur CD mesure 1,7 m.
Le triangle DIC est rectangle en I. Comme I est sur [BC], BI + IC = BC.
D'où : IC = BC − BI = 3,2 m − 2,4 m = 0,8 m.
Par ailleurs, ID = AB = 1,5 m.
D'après le théorème de Pythagore, on a : ID2 + IC2 = DC2.
D'où : DC =
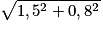m = 1,7 m.La longueur CD mesure 1,7 m.
b) Aire du toit
Le toit est rectangulaire, son aire est donc : ACDHG = CD × DH = 1,7 m × 4,8 m = 8,16 m2.
L'aire du toit est 8,16 m2.
Le toit est rectangulaire, son aire est donc : ACDHG = CD × DH = 1,7 m × 4,8 m = 8,16 m2.
L'aire du toit est 8,16 m2.
c) Pente du toit
Dans le triangle CDI, rectangle en I, on a :
tan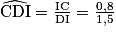
. D'où : 
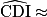28°.
La pente du toit est d'environ 28°.
Dans le triangle CDI, rectangle en I, on a :
tan
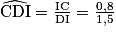. D'où : 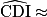28°.La pente du toit est d'environ 28°.
3.
a) Représentation du quadrilatère ABCD à l'échelle 1/50
Les mesures utiles à la construction du trapèze sont celles de AB, AD et BC. À l'échelle 1/50, ces mesures sont divisées par 50, on obtient donc :
A'B' = 1,5 m ÷ 50 = 0,03 m = 3 cm.
A'D' = 2,4 m ÷ 50 = 0,048 m = 4,8 cm.
B'C' = 3,2 m ÷ 50 = 0,064 m = 6,4 cm.
Les mesures utiles à la construction du trapèze sont celles de AB, AD et BC. À l'échelle 1/50, ces mesures sont divisées par 50, on obtient donc :
A'B' = 1,5 m ÷ 50 = 0,03 m = 3 cm.
A'D' = 2,4 m ÷ 50 = 0,048 m = 4,8 cm.
B'C' = 3,2 m ÷ 50 = 0,064 m = 6,4 cm.
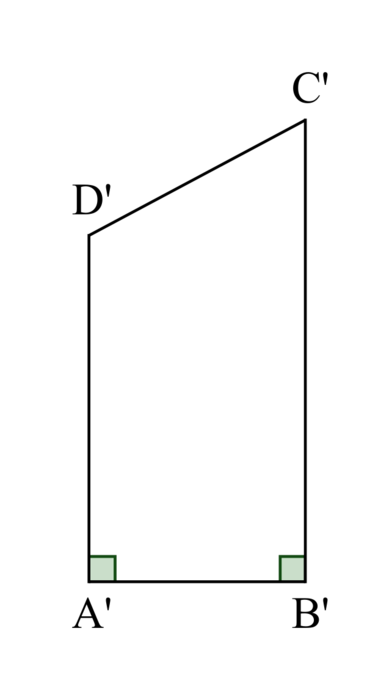 Remarque : la figure n'est pas aux dimensions attendues. |
b) Aire du trapèze ABCD
AABCD =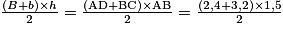
m2 = 4,2 m2.
Le trapèze ABCD a une aire de 4,2 m2.
AABCD =
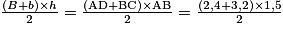m2 = 4,2 m2.Le trapèze ABCD a une aire de 4,2 m2.
c) Stockage des 15 stères de bois
Calculons le volume de l'appentis, qui a la forme d'un prisme droit de base ABCD.
VABCDEFGH = AABCD × h = 4,2 m2 × 4,8 m = 20,16 m3.
On a : 20,16 > 15.
L'appentis est suffisamment grand pour contenir les 15 stères de bois.
Calculons le volume de l'appentis, qui a la forme d'un prisme droit de base ABCD.
VABCDEFGH = AABCD × h = 4,2 m2 × 4,8 m = 20,16 m3.
On a : 20,16 > 15.
L'appentis est suffisamment grand pour contenir les 15 stères de bois.
B. Réalisation de la dalle
1. Nombre de voyages nécessaires
On creuse selon le rectangle ABFE à une profondeur de 25 cm. Le volume de terre extrait est donc, en m3 : Vterre extrait = AB × AE × 0,25 = 1,5 × 4,8 × 0,25 = 1,8 (en m3).
Le volume obtenu correspond au volume extrait, augmenté de 30 %, donc multiplié par 1,3.
On a donc : Vterre obtenu = Vterre extrait × 1,3 = 1,8 m3 × 1,3 = 2,34 m3.
On a : 2,34 ÷ 0,7
3,34.
Il faudra faire au moins quatre voyages pour évacuer la terre.
On creuse selon le rectangle ABFE à une profondeur de 25 cm. Le volume de terre extrait est donc, en m3 : Vterre extrait = AB × AE × 0,25 = 1,5 × 4,8 × 0,25 = 1,8 (en m3).
Le volume obtenu correspond au volume extrait, augmenté de 30 %, donc multiplié par 1,3.
On a donc : Vterre obtenu = Vterre extrait × 1,3 = 1,8 m3 × 1,3 = 2,34 m3.
On a : 2,34 ÷ 0,7
3,34.Il faudra faire au moins quatre voyages pour évacuer la terre.
2.
a) Prix facturé pour 8 m3 de béton
• Entrepreneur A :
Il faut prévoir deux camions toupie.
Le prix est alors : 98 € × 8 + 2 × 150 € = 1 084 €.
Il faut prévoir deux camions toupie.
Le prix est alors : 98 € × 8 + 2 × 150 € = 1 084 €.
• Entrepreneur B :
Un seul camion toupie suffit.
Le prix est : 75 € × 8 + 240 € = 840 €.
Un seul camion toupie suffit.
Le prix est : 75 € × 8 + 240 € = 840 €.
Pour 8 m3 de béton livré, l'entrepreneur A facture 1 084 € alors que l'entrepreneur B facture 840 €.
b) Correspondance entre courbes et fonctions
Pour un volume x, compris entre 0 et 7 m3, de béton livré, on a : f(x) = 98x + 150 et g(x) = 75x + 240. D'où g(0) > f(0).
La droite d2 représente donc g et la droite d1 représente f.
Pour un volume x, compris entre 0 et 7 m3, de béton livré, on a : f(x) = 98x + 150 et g(x) = 75x + 240. D'où g(0) > f(0).
La droite d2 représente donc g et la droite d1 représente f.
c) Volume maximum de béton pouvant être commandé avec 600 euros (lecture graphique)
Avec 600 €, on peut commander environ 4,75 m3 de béton.
Avec 600 €, on peut commander environ 4,75 m3 de béton.
Remarque
On lit la réponse sur le graphique en cherchant les points des droites représentées ayant pour ordonnée 600 ; la plus grande abscisse fournit la réponse.d) Choix de l'entrepreneur le moins cher et prix de la dalle
Le volume de béton à couler pour la dalle de l'appentis correspond au volume de terre extrait, soit 1,8 m3. On voit, par lecture graphique, que c'est l'entrepreneur A le moins cher.
Le prix à payer sera donc : 98 € × 1,8 + 150 € = 326,40 €.
Le volume de béton à couler pour la dalle de l'appentis correspond au volume de terre extrait, soit 1,8 m3. On voit, par lecture graphique, que c'est l'entrepreneur A le moins cher.
Le prix à payer sera donc : 98 € × 1,8 + 150 € = 326,40 €.
e) Volume de béton (entre 0 et 7 m3) à partir duquel il est préférable de changer d'entrepreneur
On voit sur le graphique que c'est d'abord l'entrepreneur A le moins cher, puis l'entrepreneur B. Déterminons pour quel volume livré les deux entrepreneurs pratiquent le même prix. Il faut résoudre f(x) = g(x), soit : 8x + 150 = 75x + 240. D'où : 23x = 90.
Et donc : x =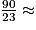
3,9.
Il faut changer d'entrepreneur à partir de 4 m3 de béton livré.
On voit sur le graphique que c'est d'abord l'entrepreneur A le moins cher, puis l'entrepreneur B. Déterminons pour quel volume livré les deux entrepreneurs pratiquent le même prix. Il faut résoudre f(x) = g(x), soit : 8x + 150 = 75x + 240. D'où : 23x = 90.
Et donc : x =
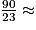3,9.Il faut changer d'entrepreneur à partir de 4 m3 de béton livré.
Deuxième partie
Exercice 1
1. Tracé de la figure obtenue
 |
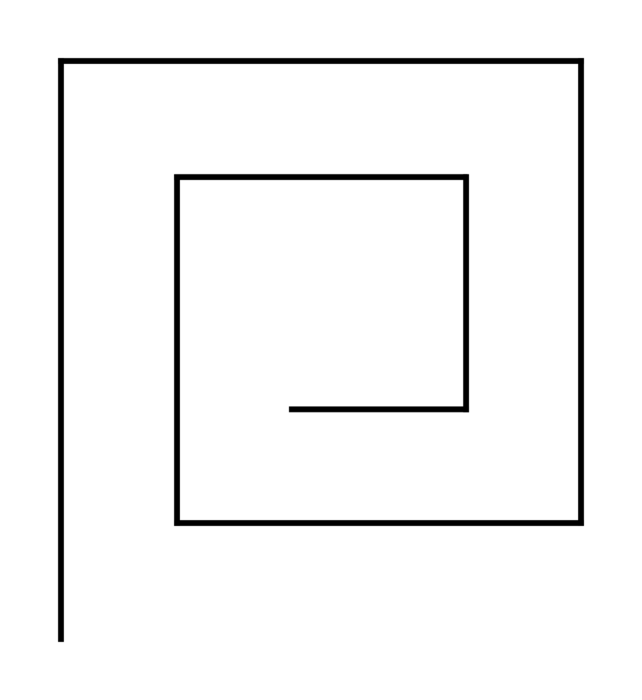La figure ci-dessus n'est pas aux dimensions attendues, mais à l'échelle. Le segment le plus court doit mesurer 3 cm ; chaque segment mesurant 1 cm de plus que le précédent, le segment le plus extérieur mesure 10 cm.
2. Figure obtenue si on supprime la ligne 6 du programme
Si on supprime la ligne 6 du programme, on obtient un carré de côté 20, le stylo repassant une fois sur le tracé…
Si on supprime la ligne 6 du programme, on obtient un carré de côté 20, le stylo repassant une fois sur le tracé…
3. Modifications du programme pour obtenir un octogone régulier de longueur de côté 40
Si l'on veut obtenir un octogone régulier de côté 40, il faut supprimer la ligne 6 du programme et modifier la ligne 3 en remplaçant « 20 » par « 40 ».
Déterminons l'angle à renseigner ligne 8 :
Soit ABCDEFGH un octogone régulier, de centre O.
Si l'on veut obtenir un octogone régulier de côté 40, il faut supprimer la ligne 6 du programme et modifier la ligne 3 en remplaçant « 20 » par « 40 ».
Déterminons l'angle à renseigner ligne 8 :
Soit ABCDEFGH un octogone régulier, de centre O.
 |
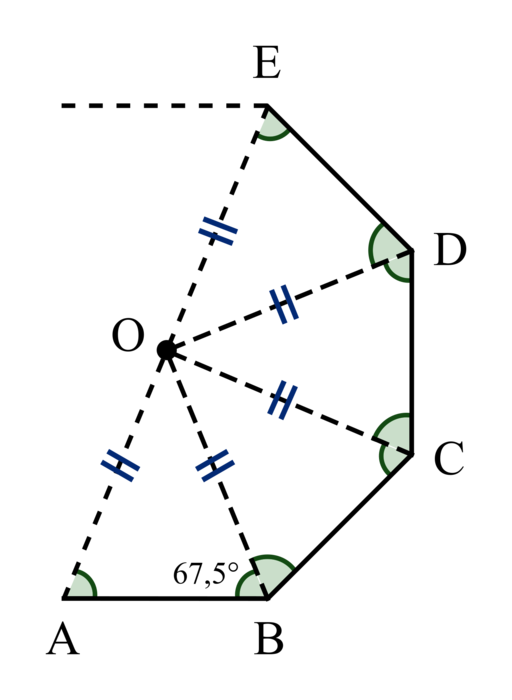On sait alors que les angles 
, 
, 
, 
, 
, 
, 
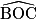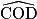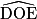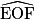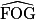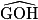et 
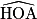sont tous égaux et de mesure : 
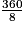= 45°. Par ailleurs, les triangles AOB, BOC, …, HOA sont tous isocèles et superposables. Leurs angles à la base valent donc : 
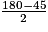= 67,5°.
Si l'on suppose que le côté AB est horizontal et que l'on commence le tracé en A, il faut donc tourner vers la gauche, en arrivant à B, d'un angle de 180° − 2 × 67,5° = 45°.
Les modifications à apporter au programme sont donc :
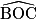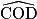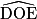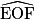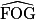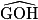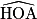, , , , , , et sont tous égaux et de mesure : 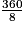= 45°. Par ailleurs, les triangles AOB, BOC, …, HOA sont tous isocèles et superposables. Leurs angles à la base valent donc : 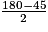= 67,5°.Si l'on suppose que le côté AB est horizontal et que l'on commence le tracé en A, il faut donc tourner vers la gauche, en arrivant à B, d'un angle de 180° − 2 × 67,5° = 45°.
Les modifications à apporter au programme sont donc :
- supprimer la ligne 6 ;
- remplacer « 20 » par « 40 » à la ligne 3 ;
- remplacer « 90 » par « 45 » à la ligne 8.
Exercice 2
1. Vitesse retenue pour un véhicule de vitesse moyenne 123 km/h
On a : 123 km/h > 100 km/h, il faut donc diminuer la vitesse de 5 % pour obtenir la vitesse retenue. 123 × 0,95 = 116,85.
La vitesse retenue sera 116,85 km/h.
On a : 123 km/h > 100 km/h, il faut donc diminuer la vitesse de 5 % pour obtenir la vitesse retenue. 123 × 0,95 = 116,85.
La vitesse retenue sera 116,85 km/h.
2. Vitesse retenue pour un véhicule ayant mis 4 minutes pour parcourir la distance entre deux points d'enregistrement
Le véhicule a mis 4 minutes pour parcourir 5,1 km.
1 h = 15 × 4 min. En une heure, le véhicule parcourrait 15 × 5,1 km, soit 76,5 km.
La vitesse réelle du véhicule est donc 76,5 km/h.
Cette vitesse étant inférieure à 100 km/h, la vitesse retenue sera 76,5 km/h − 5 km/h = 71,5 km/h.
Le véhicule a mis 4 minutes pour parcourir 5,1 km.
1 h = 15 × 4 min. En une heure, le véhicule parcourrait 15 × 5,1 km, soit 76,5 km.
La vitesse réelle du véhicule est donc 76,5 km/h.
Cette vitesse étant inférieure à 100 km/h, la vitesse retenue sera 76,5 km/h − 5 km/h = 71,5 km/h.
3. Vitesse moyenne calculée correspondant à une vitesse retenue de 114 km/h
La vitesse retenue étant supérieure à 100 km/h, la vitesse calculée l'était aussi. La vitesse retenue a donc été obtenue à partir de la vitesse calculée en multipliant cette dernière par 0,95, ce qui correspond à une diminution de 5 %. Pour obtenir la vitesse calculée à partir de la vitesse retenue, il suffit donc de diviser la vitesse retenue par 0,95.
114 ÷ 0,95 = 120.
La vitesse calculée était de 120 km/h.
La vitesse retenue étant supérieure à 100 km/h, la vitesse calculée l'était aussi. La vitesse retenue a donc été obtenue à partir de la vitesse calculée en multipliant cette dernière par 0,95, ce qui correspond à une diminution de 5 %. Pour obtenir la vitesse calculée à partir de la vitesse retenue, il suffit donc de diviser la vitesse retenue par 0,95.
114 ÷ 0,95 = 120.
La vitesse calculée était de 120 km/h.
4. Sanction potentielle du conducteur
Calculons la durée du trajet entre les deux radars :
9 h 22 min 7 s − 9 h 17 min 56 s = 4 min 11 s = 251 s.
La vitesse du véhicule est donc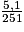
km/s soit 
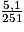× 3 600 km/h 
73,15 km/h.
La vitesse retenue, après retrait de 5 km/h, sera inférieure à 70 km/h.
Le conducteur ne sera donc pas sanctionné par une contravention.
Calculons la durée du trajet entre les deux radars :
9 h 22 min 7 s − 9 h 17 min 56 s = 4 min 11 s = 251 s.
La vitesse du véhicule est donc
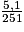km/s soit 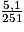× 3 600 km/h 73,15 km/h.La vitesse retenue, après retrait de 5 km/h, sera inférieure à 70 km/h.
Le conducteur ne sera donc pas sanctionné par une contravention.
Exercice 3
Calculons la masse volumique du cube choisi.
Son volume est : 53 cm3 = 125 cm3 = 125 × 10−6 m3.
Sa masse est : 1 110 g = 1,11 kg.
La masse volumique du cube est donc :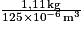
= 8 880 kg/m3. Ce résultat est très proche de celui annoncé pour le nickel.
Le cube choisi est en nickel.
Son volume est : 53 cm3 = 125 cm3 = 125 × 10−6 m3.
Sa masse est : 1 110 g = 1,11 kg.
La masse volumique du cube est donc :
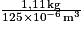= 8 880 kg/m3. Ce résultat est très proche de celui annoncé pour le nickel.Le cube choisi est en nickel.
Exercice 4
1. Âge médian des membres du club
La répartition par années d'âge des membres du club est la suivante :
Le club comporte donc : 1 + 4 + 7 + 4 + 4 + 8 + 16 + 10 + 6 = 60 membres.
60 ÷ 2 = 30. La valeur médiane est donc comprise entre la 30e et la 31e valeur, les valeurs étant rangées par ordre croissant.
1 + 4 + 7 + 4 + 4 + 8 = 28 < 30
1 + 4 + 7 + 4 + 4 + 8 + 16 = 44 > 30
Les 30e et 31e valeurs sont donc égales à 20.
L'âge médian des membres du club est donc 20 ans.
La répartition par années d'âge des membres du club est la suivante :
| Âge (en années) | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
|---|---|---|---|---|---|---|---|---|---|
| Nombre de personnes | 1 | 4 | 7 | 4 | 4 | 8 | 16 | 10 | 6 |
Le club comporte donc : 1 + 4 + 7 + 4 + 4 + 8 + 16 + 10 + 6 = 60 membres.
60 ÷ 2 = 30. La valeur médiane est donc comprise entre la 30e et la 31e valeur, les valeurs étant rangées par ordre croissant.
1 + 4 + 7 + 4 + 4 + 8 = 28 < 30
1 + 4 + 7 + 4 + 4 + 8 + 16 = 44 > 30
Les 30e et 31e valeurs sont donc égales à 20.
L'âge médian des membres du club est donc 20 ans.
2. Pourcentage de membres de moins de 18 ans
On a : 1 + 4 + 7 + 4 = 16. Il y a 16 personnes de moins de 18 ans au club.
D'où :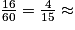
0,27.
Environ 27 % des membres du club ont moins de 18 ans.
On a : 1 + 4 + 7 + 4 = 16. Il y a 16 personnes de moins de 18 ans au club.
D'où :
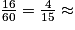0,27.Environ 27 % des membres du club ont moins de 18 ans.
3.
a) Probabilité pour que le gagnant ait 22 ans
On a :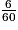
= 0,1.
La probabilité pour que le gagnant ait 22 ans est 0,1.
On a :
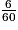= 0,1.La probabilité pour que le gagnant ait 22 ans est 0,1.
b) Probabilité pour que le gagnant ait au moins 18 ans
Nous avons vu plus haut (question 2.) que 16 membres du club ont moins de 18 ans.
60 − 16 = 44. Il y a donc 44 membres du club qui ont au moins 18 ans.
D'où :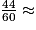
0,73.
La probabilité pour que le gagnant ait au moins 18 ans est d'environ 0,73.
Nous avons vu plus haut (question 2.) que 16 membres du club ont moins de 18 ans.
60 − 16 = 44. Il y a donc 44 membres du club qui ont au moins 18 ans.
D'où :
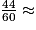0,73.La probabilité pour que le gagnant ait au moins 18 ans est d'environ 0,73.
Troisième partie
Situation 1
1. Notion mathématique travaillée
Comme il est supposé que toutes les oranges fournissent la même quantité de jus, le volume de jus produit est proportionnel au nombre d'oranges pressées.
La notion mathématique travaillée ici est la proportionnalité.
Comme il est supposé que toutes les oranges fournissent la même quantité de jus, le volume de jus produit est proportionnel au nombre d'oranges pressées.
La notion mathématique travaillée ici est la proportionnalité.
2. Trois procédures élèves possibles en CM2
• Procédure 1 : utilisation de la linéarité multiplicative
On calcule le jus produit par 3 oranges, en observant que 3 = 6 ÷ 2.
300 ÷ 2 = 150.
3 oranges produisent 150 mL de jus.
On observe ensuite que 9 = 3 × 3. D'où : 150 × 3 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
On calcule le jus produit par 3 oranges, en observant que 3 = 6 ÷ 2.
300 ÷ 2 = 150.
3 oranges produisent 150 mL de jus.
On observe ensuite que 9 = 3 × 3. D'où : 150 × 3 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
• Procédure 2 : utilisation de la linéarité multiplicative et de la linéarité additive
On calcule le jus produit par 3 oranges, en observant que 3 = 6 ÷ 2.
300 ÷ 2 = 150.
3 oranges produisent 150 mL de jus.
On observe ensuite que : 9 = 3 + 6. D'où : 150 + 300 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
On calcule le jus produit par 3 oranges, en observant que 3 = 6 ÷ 2.
300 ÷ 2 = 150.
3 oranges produisent 150 mL de jus.
On observe ensuite que : 9 = 3 + 6. D'où : 150 + 300 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
• Procédure 3 : utilisation de la linéarité multiplicative pour passer à l'unité (règle de trois)
On calcule le jus produit par 1 orange :
300 ÷ 6 = 50.
1 orange produit 50 mL de jus.
D'où : 9 × 50 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
On calcule le jus produit par 1 orange :
300 ÷ 6 = 50.
1 orange produit 50 mL de jus.
D'où : 9 × 50 = 450.
On conclut que 9 oranges produisent 450 mL de jus.
3. Modification de l'énoncé pour favoriser le passage à l'unité
À partir des mêmes données, il suffit de poser la question pour un nombre d'oranges n'ayant pas de diviseur commun avec 6, par exemple 7 (ou 5, 11…).
À partir des mêmes données, il suffit de poser la question pour un nombre d'oranges n'ayant pas de diviseur commun avec 6, par exemple 7 (ou 5, 11…).
Situation 2
1. Analyse de production d'élèves (réussites et éventuelles erreurs)
Remarque
Pour ce type de questions, il est recommandé de présenter la réponse à l'aide d'un tableau. La réponse gagne en lisibilité et la candidate ou le candidat s'assure qu'elle/il a bien abordé tous les aspects de la question…| Description de la démarche | Réussites | Éventuelles erreurs | |
|---|---|---|---|
| A | L'élève pose les opérations. Il additionne 50 et 8 et observe sûrement que le résultat est trop éloigné de la cible ; il barre donc son calcul, puis pose l'addition de 25 et 75. Il obtient 100, auquel il retranche 10. Le résultat, 10, est erroné. | L'élève semble avoir compris les enjeux de la situation. Il sait poser et effectuer une addition de deux entiers. Il sait comparer des entiers. | Il se trompe dans la soustraction posée. On peut d'ailleurs considérer que c'est une erreur de poser ce type de calcul, qui doit/devrait être effectué mentalement… |
| B | Après une ébauche de calcul de la somme de 75 et 10, l'élève pose et effectue la somme de 50 et 25, puis de 75 et 8, pour finir par le calcul, non achevé, de 83 et 4. | L'élève semble avoir compris les enjeux de la situation. Il sait poser et effectuer une addition de deux entiers. Il sait comparer des entiers. | Il n'y a pas d'erreur, mais l'élève ne trouve pas la solution… |
| C | L'élève calcule en ligne la somme de 75 et 25, puis la différence entre 10 et 8 et enfin la différence entre 100 et 2. | L'élève a compris les enjeux de la situation. Il sait effectuer en ligne la somme et la différence de deux entiers. L'écriture en ligne de la somme 75 + 25 est peut-être (sûrement ?) la transcription de la connaissance du fait numérique. Il sait comparer des entiers. | Pas d'erreur. L'élève a trouvé une solution. |
| D | L'élève calcule en ligne le produit de 25 et 4, puis les différences entre 10 et 8, et 100 et 2. | L'élève a compris les enjeux de la situation. Il sait effectuer en ligne le produit et la différence de deux entiers. L'écriture en ligne du produit 25 × 4 est peut-être (sûrement ?) la transcription de la connaissance du fait numérique. Il sait comparer des entiers. | Pas d'erreur. L'élève a trouvé une solution. |
2. Faits numériques connus des élèves C et D
L'élève D connaît la décomposition multiplicative : 100 = 4 × 25.
L'élève C connaît la décomposition additive : 100 = 25 + 75.
L'élève D connaît la décomposition multiplicative : 100 = 4 × 25.
L'élève C connaît la décomposition additive : 100 = 25 + 75.
3. Exercice de réinvestissement des multiples de 9 et deux solutions possibles
On peut proposer « 34 » pour cible, avec le tirage : 9 – 6 – 4 – 27 – 18 – 8.
Deux solutions possibles sont alors :
Solution 1 : 4 × 9 = 36 ; 8 − 6 = 2 ; 36 − 2 = 34.
Solution 2 : 9 + 27 = 36 ; 8 − 6 = 2 ; 36 − 2 = 34.
On peut proposer « 34 » pour cible, avec le tirage : 9 – 6 – 4 – 27 – 18 – 8.
Deux solutions possibles sont alors :
Solution 1 : 4 × 9 = 36 ; 8 − 6 = 2 ; 36 − 2 = 34.
Solution 2 : 9 + 27 = 36 ; 8 − 6 = 2 ; 36 − 2 = 34.
Remarque
Une façon « économique » de répondre à la question posée consiste à observer les relations arithmétiques entre les données proposées et de les reproduire, en remplaçant 25 (= 5 × 5) par 9 (= 3 × 3). On obtient ainsi des procédures de même type que celles des élèves C (solution 2) et D (solution 1).4. Deux avantages et deux points de vigilance quant à la mise en œuvre d'une activité type « compte est bon »
Avantages :
Avantages :
- L'activité permet de mobiliser et développer les connaissances de faits numériques et le calcul réfléchi.
- Le défi proposé est motivant.
- L'activité développe le sens de la recherche et la persévérance.
- L'enseignant doit veiller à ce que tous les élèves aient bien compris l'objectif et les « règles du jeu ».
- L'enseignant doit être attentif à ne pas provoquer le découragement d'élèves peu outillés en faits numériques mémorisés, qui pourraient renoncer devant l'ampleur de la tâche et la multiplicité des essais pouvant potentiellement être faits.
Situation 3
1. Complémentarité du calcul en ligne et du calcul mental
Le calcul mental permet soit l'entraînement strict à la mémorisation des faits numériques, soit l'entraînement au calcul réfléchi, qui mobilise, quant à lui, à la fois des connaissances des faits numériques, de la numération et des propriétés opératoires. Les calculs réfléchis opérés strictement mentalement ne peuvent toutefois pas être trop longs ou complexes, ils sont limités par les capacités de mise en mémoire de travail.
Le calcul en ligne est également du calcul réfléchi, mais les calculs peuvent être plus longs et/ou complexes car les résultats intermédiaires sont écrits. Par ailleurs, le fait que les étapes de calcul soient écrites permet un retour sur les procédures de calcul et ainsi de les confronter d'une part et d'expliciter les propriétés et faits numériques mobilisés d'autre part.
Le calcul mental permet soit l'entraînement strict à la mémorisation des faits numériques, soit l'entraînement au calcul réfléchi, qui mobilise, quant à lui, à la fois des connaissances des faits numériques, de la numération et des propriétés opératoires. Les calculs réfléchis opérés strictement mentalement ne peuvent toutefois pas être trop longs ou complexes, ils sont limités par les capacités de mise en mémoire de travail.
Le calcul en ligne est également du calcul réfléchi, mais les calculs peuvent être plus longs et/ou complexes car les résultats intermédiaires sont écrits. Par ailleurs, le fait que les étapes de calcul soient écrites permet un retour sur les procédures de calcul et ainsi de les confronter d'une part et d'expliciter les propriétés et faits numériques mobilisés d'autre part.
2. Procédures utilisées et erreurs éventuelles des élèves
Amina associe, de la droite vers la gauche, les chiffres des deux termes de la somme écrite. Ce faisant, elle ne tient pas compte des positions relatives aux unités de numération des chiffres pris en compte. Elle additionne ainsi 7 centièmes avec 7 dixièmes, 4 dixièmes avec 2 entiers. Elle convertit toutefois correctement les 14 centièmes qu'elle obtient en 1 dixième (qu'elle ajoute aux 6 dixièmes obtenus par ailleurs) et 4 centièmes.
Au niveau opératoire, elle traite donc 2,7 comme 0,27. À cette erreur près, son calcul est juste.
Tony décompose mentalement 2,7 en 2 + 0,7 et ajoute, toujours mentalement, 2 à 12,47. Il effectue ensuite mentalement la somme 14,47 + 0,7. Il n'y a pas d'erreur.
Zoé décompose mentalement en unités de numération et ajoute 2 entiers à 12 entiers et 7 dixièmes à 4 dixièmes. Elle omet toutefois de convertir les 11 dixièmes obtenus en 1 unité et 1 dixième. Elle écrit la réponse, erronée, 14,117.
Ugo opère mentalement la somme en traitant 2,7 comme 2,07. Il obtient ainsi 14 centièmes, qu'il convertit correctement en 1 dixième et 4 centièmes. Le reste du calcul est cohérent, même si le résultat (14,54) est erroné.
Amina associe, de la droite vers la gauche, les chiffres des deux termes de la somme écrite. Ce faisant, elle ne tient pas compte des positions relatives aux unités de numération des chiffres pris en compte. Elle additionne ainsi 7 centièmes avec 7 dixièmes, 4 dixièmes avec 2 entiers. Elle convertit toutefois correctement les 14 centièmes qu'elle obtient en 1 dixième (qu'elle ajoute aux 6 dixièmes obtenus par ailleurs) et 4 centièmes.
Au niveau opératoire, elle traite donc 2,7 comme 0,27. À cette erreur près, son calcul est juste.
Tony décompose mentalement 2,7 en 2 + 0,7 et ajoute, toujours mentalement, 2 à 12,47. Il effectue ensuite mentalement la somme 14,47 + 0,7. Il n'y a pas d'erreur.
Zoé décompose mentalement en unités de numération et ajoute 2 entiers à 12 entiers et 7 dixièmes à 4 dixièmes. Elle omet toutefois de convertir les 11 dixièmes obtenus en 1 unité et 1 dixième. Elle écrit la réponse, erronée, 14,117.
Ugo opère mentalement la somme en traitant 2,7 comme 2,07. Il obtient ainsi 14 centièmes, qu'il convertit correctement en 1 dixième et 4 centièmes. Le reste du calcul est cohérent, même si le résultat (14,54) est erroné.
3. Étayage possible pour aider Zoé à corriger son erreur
La seule erreur de Zoé étant l'absence de conversion des 11 dixièmes obtenus, un premier étayage peut consister en un dialogue avec l'élève, l'amenant à verbaliser ce résultat intermédiaire obtenu et la mettant sur la voie de la conversion de 10 dixièmes en une unité. Un second étayage pourrait consister en la mise à disposition de matériel de numération, permettant la matérialisation de la somme à opérer et des étapes du calcul, tout en les explicitant.
La seule erreur de Zoé étant l'absence de conversion des 11 dixièmes obtenus, un premier étayage peut consister en un dialogue avec l'élève, l'amenant à verbaliser ce résultat intermédiaire obtenu et la mettant sur la voie de la conversion de 10 dixièmes en une unité. Un second étayage pourrait consister en la mise à disposition de matériel de numération, permettant la matérialisation de la somme à opérer et des étapes du calcul, tout en les explicitant.
Document précédent
Sujet 2019, groupement académique 1
Document suivant
Sujet 2019, groupement académique 3