Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
L'indice de masse corporelle (IMC) est une grandeur qui permet d'estimer la corpulence d'une personne en fonction de sa taille et de sa masse corporelle afin d'évaluer les risques liés au surpoids.
| Voici la formule permettant de calculer l'indice de masse corporelle : IMC = 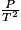 dans laquelle : IMC désigne l'indice de masse corporelle exprimée en kilogrammes par mètre carré (kg/m2) ; P désigne la masse exprimée en kilogrammes (kg) ; T désigne la taille exprimée en mètres (m). |
A. Utilisation et interprétation de l'indice de masse corporelle chez l'adulte
Pour prévenir les risques liés aux problèmes de poids, l'Organisation mondiale de la santé a défini les intervalles standards suivants :
| IMC (kg/m2) | Interprétation |
|---|---|
| moins de 16,5 | anorexie |
| de 16,5 à moins de 18,5 | maigreur |
| de 18,5 à moins de 25 | corpulence normale |
| de 25 à moins de 30 | surpoids |
| de 30 à moins de 35 | obésité modérée |
| de 35 à moins de 40 | obésité sévère |
| plus de 40 | obésité morbide |
1. Claire mesure 160 cm et pèse 53 kg. Calculer son IMC. Quelle interprétation peut-on en faire ?
2. On interroge huit hommes sur leur masse et leur taille afin de calculer leur IMC.
On obtient le tableau suivant :
On obtient le tableau suivant :
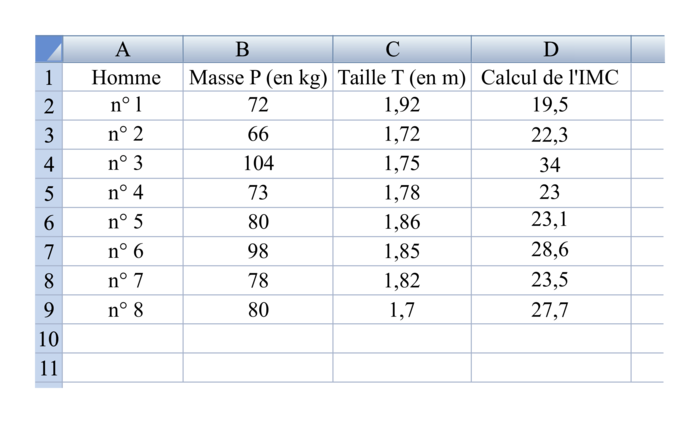 |
a) Quelle formule a pu être écrite en D2 puis étirée jusqu'en D9 pour calculer l'IMC ?
b) Parmi ceux qui ont été interrogés, quel est le pourcentage d'hommes « obèses » ou « en surpoids » ?
3. Une personne a un IMC de 28 et pèse 70 kg. Combien de kilogrammes doit-elle perdre pour avoir un IMC de 25 ?
4. Quelle masse minimale et quelle masse maximale peut avoir une personne mesurant 1,72 m pour avoir une « corpulence normale » ?
B. L'obésité et le surpoids en France
En 2012, une enquête nationale sur l'obésité et le surpoids a été réalisée en France sur un échantillon de 25 714 personnes de 18 ans et plus.
Le tableau ci-dessous indique les résultats obtenus.
Le tableau ci-dessous indique les résultats obtenus.
| Femmes | Hommes | ||
|---|---|---|---|
| Pas de surpoids | IMC < 25 | 7 830 | 5 728 |
| Surpoids | 25  IMC < 30 IMC < 30 | 3 551 | 4 739 |
| Obésité | 30  IMC IMC | 2 119 | 1 747 |
| Total | 13 500 | 12 214 |
Une société proposant des solutions pour mincir décide d'entreprendre un démarchage téléphonique pour se constituer une clientèle.
Elle appelle au hasard une personne de plus de 18 ans.
On considérera que la répartition de la population pouvant être appelée est dans la même proportion que celle de cet échantillon.
On donnera les réponses en pourcentage arrondi à l'unité.
Elle appelle au hasard une personne de plus de 18 ans.
On considérera que la répartition de la population pouvant être appelée est dans la même proportion que celle de cet échantillon.
On donnera les réponses en pourcentage arrondi à l'unité.
1. Quelle est la probabilité que cette personne soit en surpoids ou obèse ?
2. La personne appelée est un homme. Quelle est la probabilité que cet homme soit en surpoids ou obèse ?
3. La personne appelée est obèse. Quelle est la probabilité que cette personne soit un homme ?
4. Une personne prétend que plus de 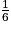 de l'échantillon est obèse. A-t-elle raison ? Justifier.
de l'échantillon est obèse. A-t-elle raison ? Justifier.
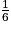 de l'échantillon est obèse. A-t-elle raison ? Justifier.
de l'échantillon est obèse. A-t-elle raison ? Justifier.C. Utilisation et interprétation de l'indice de masse corporelle chez l'enfant
Au départ, l'IMC a été conçu pour les adultes de 18 ans et plus, mais il est important de dépister précocement un simple excès de poids, qui peut, par la suite, conduire à l'obésité. L'IMC est donc aussi calculé chez les enfants. Cette valeur est reportée ensuite sur un graphique présent dans son carnet de santé et qui est spécifique au sexe de l'enfant.
Voici le graphique représentant l'évolution de l'IMC d'Emma, aujourd'hui âgée de 19 ans.
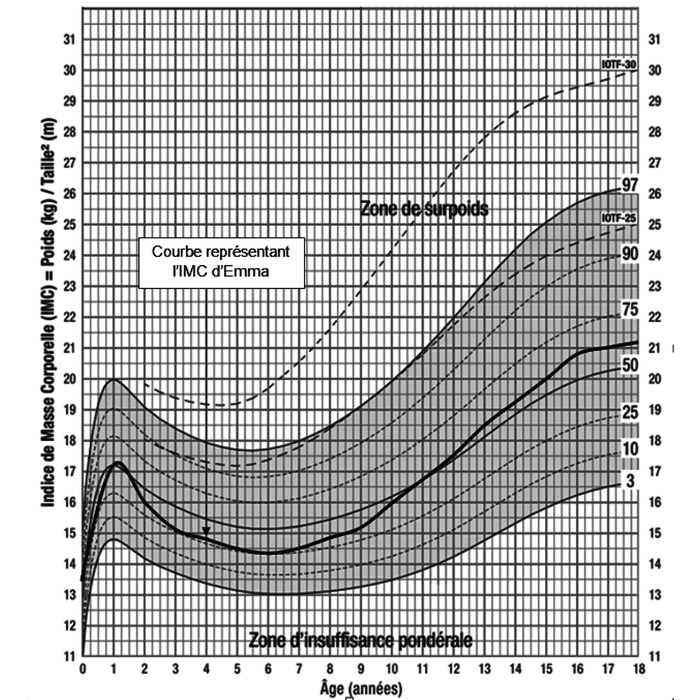 Source : http://inpes.santepubliquefrance.fr/CFESBases/catalogue/pdf/IMC/courbes_enfants.pdf |
La zone grisée représente la zone de « corpulence normale » dans laquelle la plupart des enfants se situent.
En dessous, l'enfant est considéré en insuffisance pondérale et au-dessus en surpoids.
En dessous, l'enfant est considéré en insuffisance pondérale et au-dessus en surpoids.
1. D'après ce graphique, l'IMC chez l'enfant est-il proportionnel à l'âge ? Justifier.
2.
a) À 12 ans, quel est l'IMC maximum qu'une fille doit avoir pour ne pas être considérée en surpoids ?
b) À 7 ans, entre quelles valeurs se situe l'IMC d'une fille pour qu'elle soit de corpulence normale ?
c) À partir de quel âge une fille est-elle considérée en insuffisance pondérale avec un IMC de 15 kg/m2 ?
3. Quelles sont les tranches d'âges sur lesquelles Emma avait un IMC inférieur ou égal à 16 kg/m2 ?
D. Alimentation
Les problèmes de poids peuvent être liés à l'alimentation. Il est donc intéressant de savoir lire les étiquettes des produits industriels.
Le goûter de Frédéric, 8 ans, est composé d'une portion de 30 g de gâteau et d'un verre de 200 mL de soda.
• Sur ce paquet de gâteaux, on peut lire les informations suivantes :
| Valeurs nutritionnelles moyennes | Pour 100 g |
|---|---|
| Matières grasses (lipides) dont acides gras saturés | 16 g 6,2 g |
| Glucides dont sucres | 54 g 42 g |
| Protéines | 5,5 g |
• Sur la bouteille de soda, il est indiqué que 100 mL contiennent 14,7 g de glucides dont 14,7 g de sucres et qu'il n'y a aucune matière grasse ni aucune protéine.
1. Recopier et compléter le tableau suivant.
| Valeurs nutritionnelles moyennes pour le goûter de Frédéric | 1 portion de 30 g de gâteau | 200 mL de soda | Total |
|---|---|---|---|
| Matières grasses (lipides) dont acides gras saturés | …… …… | …… …… | …… …… |
| Glucides dont sucres | …… …… | …… …… | …… …… |
| Protéines | …… | …… | …… |
2. Pour un morceau de sucre d'environ 6 g, l'apport énergétique est en moyenne de 24 kcal (kilocalories).
a) Quel est l'apport énergétique du sucre contenu dans le goûter de Frédéric ?
b) Pour un garçon de 8 ans, l'apport énergétique quotidien conseillé, pour un niveau d'activité moyen, est de 1 985 kcal.
Afin de diminuer le risque de surpoids, d'obésité et de caries dentaires, il est souhaitable, pour les adultes comme pour les enfants, que leur consommation de sucre représente au maximum 10 % de l'apport énergétique quotidien.
Source : http://www.who.int/mediacentre/news/releases/2015/sugar-guideline/fr/
À combien de morceaux de sucre correspond la masse de sucre que Frédéric ne devrait pas dépasser quotidiennement ?
Afin de diminuer le risque de surpoids, d'obésité et de caries dentaires, il est souhaitable, pour les adultes comme pour les enfants, que leur consommation de sucre représente au maximum 10 % de l'apport énergétique quotidien.
Source : http://www.who.int/mediacentre/news/releases/2015/sugar-guideline/fr/
À combien de morceaux de sucre correspond la masse de sucre que Frédéric ne devrait pas dépasser quotidiennement ?
c) Calculer le pourcentage des apports quotidiens recommandés que représente la quantité de sucre consommé par Frédéric durant son goûter.
Deuxième partie (13 points)
Cette partie est composée de trois exercices indépendants.
Exercice 1
On considère la figure ci-dessous, qui n'est pas représentée à l'échelle.
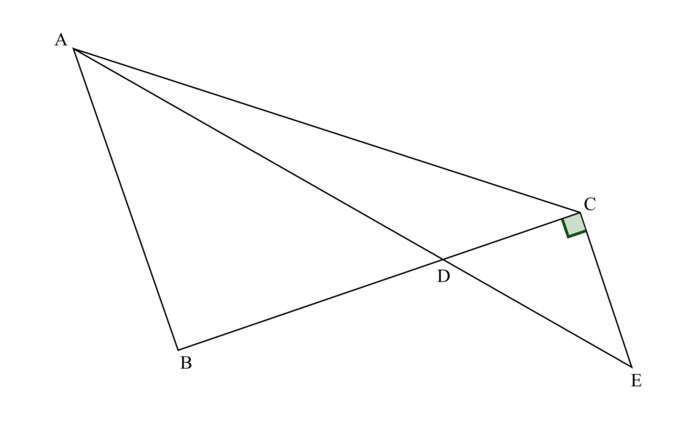 |
On sait que :
- BC = 8 cm.
- AB = 6 cm.
- AC = 10 cm.
- AD = 8 cm.
- D appartient aux segments [AE] et [BC].
- Les droites (BC) et (CE) sont perpendiculaires.
Le but de l'exercice est de déterminer l'aire du triangle ACE.
1. Montrer que les droites (AB) et (BC) sont perpendiculaires.
2. En déduire la longueur BD.
3. Déterminer la longueur CE.
4. Déterminer l'aire du triangle ACE.
Exercice 2
1. Pour tout nombre entier n, montrer que 30n + 25 est divisible par 5.
2. Voici un programme de calcul :
|
a) Montrer que ce programme a pour résultat 265 si le nombre entier choisi est 8. Les calculs seront détaillés.
b) Quel résultat obtient-on si le nombre entier choisi est (−56) ?
c) Montrer que le résultat de ce programme de calculs, quel que soit le nombre de départ, est divisible par 5.
Exercice 3
La figure ci-dessous a été réalisée à l'aide du logiciel de programmation Scratch.
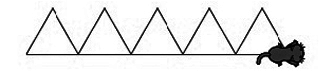 |
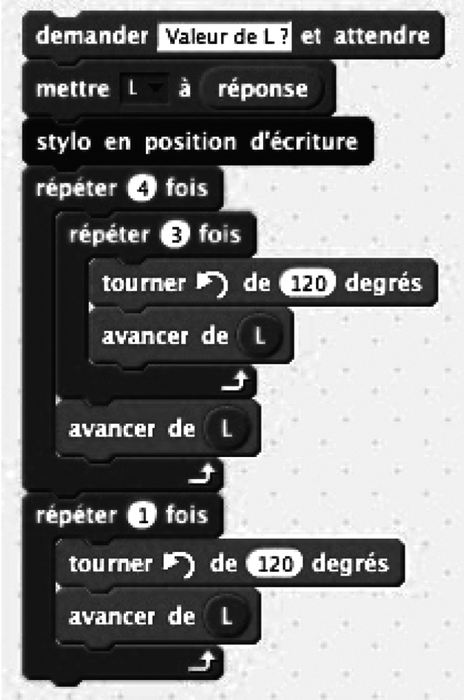
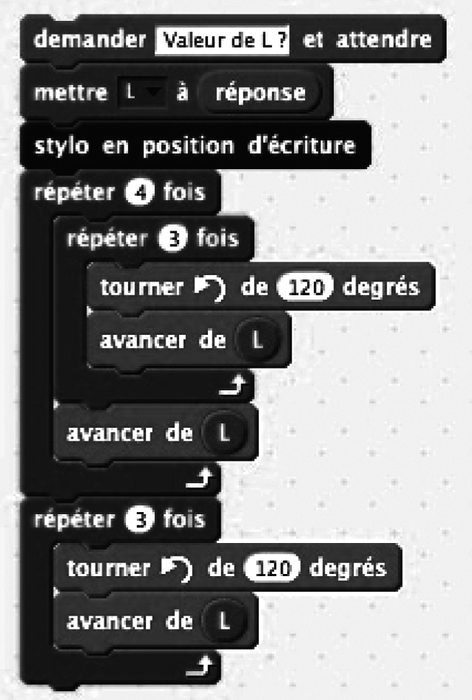
1. Parmi les programmes proposés ci-dessous, quel est celui qui permet de tracer ce dessin ? Aucune justification n'est demandée.
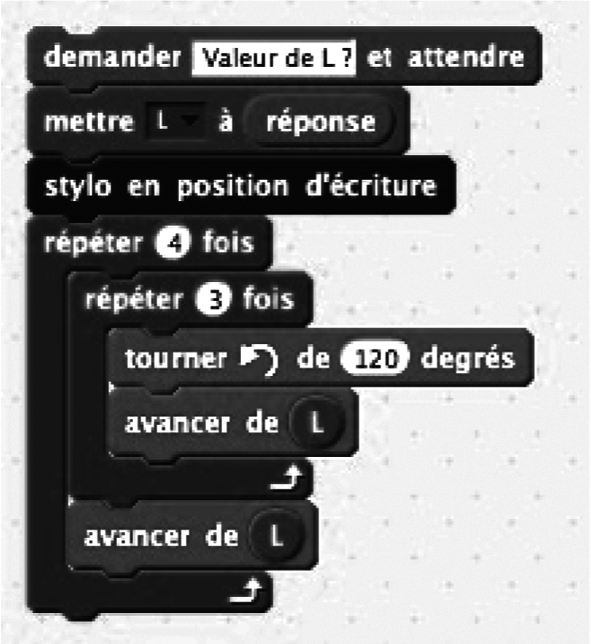 |
 |
 |
 |
2. Dans ces programmes, l'angle de rotation est de 120°. Expliquer pourquoi.
3. Tracer à main levée les figures obtenues avec chacun des programmes non retenus à la question 1.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
| Léo a 24 € dans son porte-monnaie. Il a 8 € de plus que Lilou. Combien d'euros Lilou a-t-elle ? |
Situation 1
L'exercice ci-dessous est proposé dans une classe de CE1. Les élèves doivent écouter l'énoncé du problème lu par l'enseignant, puis rechercher une réponse numérique à la question du problème pour l'entourer parmi 6 propositions. Ils doivent produire des traces de leur recherche.
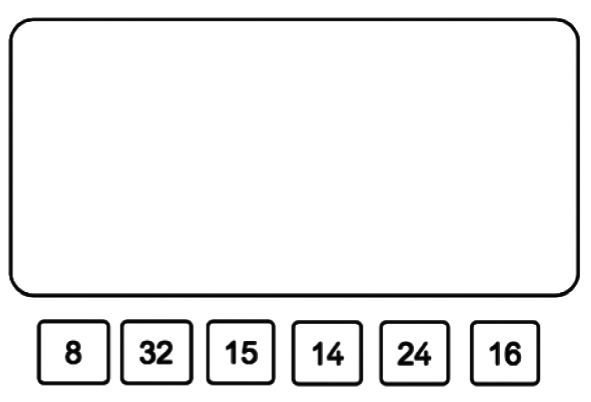 |
1. En quoi les compétences modéliser et calculer sont-elles mobilisées pour résoudre ce problème ?
2. Donner deux difficultés que les élèves pourraient rencontrer pour résoudre ce problème.
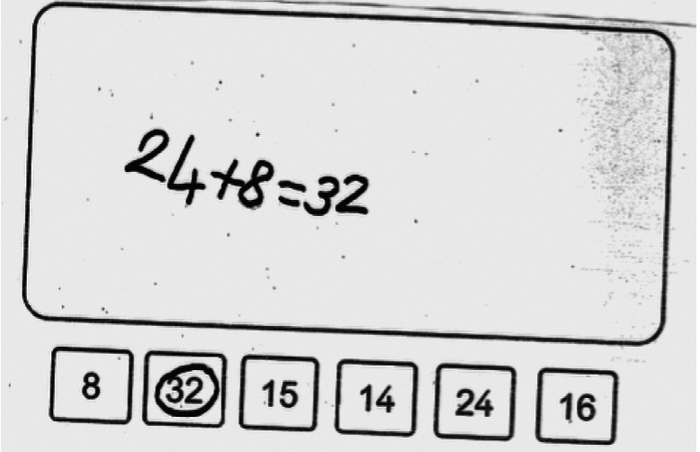
3. Voici les productions de quatre élèves.
 |
 |
 |
 |
Pour chacun de ces travaux :
a) Analyser la trace écrite (procédures suivies, compétences mises en œuvre, erreurs éventuelles).
b) Proposer une remédiation ou un accompagnement que l'enseignant pourrait mettre en place pour aider Lucas et Kiara à résoudre le problème.
4. Au cours du CE1, l'enseignant propose à nouveau l'exercice avec d'autres nombres afin de faire évoluer les représentations schématiques utilisées par les élèves.
| Léo a 322 € dans son porte-monnaie. Il a 46 € de plus que Lilou. Combien d'euros Lilou a-t-elle ? |
Proposer une représentation schématique que l'enseignant peut présenter aux élèves pour les aider à modéliser la situation.
Situation 2
Un enseignant propose à ses élèves un exercice inspiré d'une activité extraite du manuel Cap Maths CM2 (Hatier, 2010).
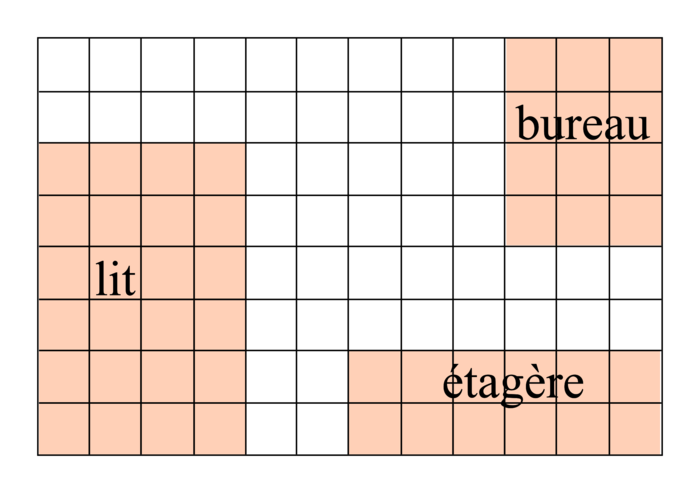
| Figurine a fait un plan de sa chambre sur un papier quadrillé pour y disposer son lit, un bureau et une étagère. La chambre est représentée par le grand rectangle de 8 carreaux sur 12 carreaux. Elle veut réaliser un agrandissement de ce plan. Elle décide que le grand côté de la chambre devra mesurer 18 carreaux sur le plan agrandi. Détermine les dimensions du plan agrandi et des meubles de la chambre sur ce plan agrandi. |
 |
1. Voici un extrait de réponse d'un élève.
| On a ajouté 6 carreaux au grand côté, il faut donc ajouter 6 carreaux à tous les côtés. […] Pour le lit : grand côté = 6 + 6 = 12 carreaux petit côté = 4 + 6 = 10 carreaux […] |
Comment, sans s'appuyer sur la bonne réponse, peut-on convaincre cet élève que sa réponse est fausse ?
2. Proposer trois procédures correctes qu'un élève de CM2 peut mettre en œuvre pour donner les dimensions correctes de l'étagère. Expliciter la propriété mathématique utilisée pour chaque procédure.
Situation 3
Un enseignant de CM2 propose les exercices suivants à ses élèves.
 |
On trouvera ci-dessous quatre productions d'élèves.
 |
 |
 |
 |
1. Dans cette question, on s'intéresse uniquement à l'exercice 1.
a) Pour chacun des élèves, décrire les réussites et les erreurs éventuelles.
b) Quelle tâche, impliquant des fractions décimales, l'enseignant pourrait proposer à Miroslav, pour l'aider à corriger ses erreurs et renforcer sa compréhension de l'écriture décimale ?
2. Dans certains anciens manuels scolaires, on trouve des exercices du type :
| Range ces nombres par ordre croissant : 7,32 – 7,35 – 12,42 – 7,57 – 12,05 – 7,01 |
En s'appuyant sur la production de Miroslav ou de Célestine, expliquer en quoi cet exercice ne permet pas d'évaluer de façon fiable la compétence « Savoir comparer deux nombres décimaux ». Puis, proposer des modifications à l'exercice afin de le rendre plus pertinent.
3. Analyser les réussites et les erreurs de Célestine à l'exercice 2.
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Utilisation et interprétation de l'indice de masse corporelle chez l'adulte
1. IMC de Claire et interprétation
Avec les notations de l'énoncé, P = 53 kg et T = 1,6 m. On a donc :
IMC =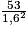 kg/m2
kg/m2  20,7 kg/m2.
20,7 kg/m2.
Claire a un IMC de 20,7 kg/m2 : elle est donc de corpulence « normale ».
Avec les notations de l'énoncé, P = 53 kg et T = 1,6 m. On a donc :
IMC =
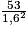 kg/m2
kg/m2  20,7 kg/m2.
20,7 kg/m2.Claire a un IMC de 20,7 kg/m2 : elle est donc de corpulence « normale ».
2.
a) Formule écrite en D2
Pour obtenir les valeurs de la colonne D à partir de la cellule D2 en l'étirant vers le bas, on peut entrer en D2 : =B2/(C2^2).
Pour obtenir les valeurs de la colonne D à partir de la cellule D2 en l'étirant vers le bas, on peut entrer en D2 : =B2/(C2^2).
Remarque
En fait, au vu des valeurs présentes dans le tableau, c'est plutôt : =ARRONDI(B2/(C2^2);1), mais ce résultat n'était certainement pas exigé.b) Pourcentage d'hommes « obèses » ou en « surpoids »
Il y a 3 hommes sur 8 qui ont un IMC supérieur ou égal à 25 kg/m2. On a :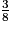 = 0,375.
= 0,375.
Le pourcentage d'hommes « obèses » ou « en surpoids » est donc 37,5 %.
Il y a 3 hommes sur 8 qui ont un IMC supérieur ou égal à 25 kg/m2. On a :
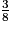 = 0,375.
= 0,375.Le pourcentage d'hommes « obèses » ou « en surpoids » est donc 37,5 %.
3. Perte de poids nécessaire pour avoir un IMC de 25
IMC = 28 kg/m2 et M = 70 kg. On en déduit que : T2 =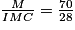 .
.
On veut : IMC = 25 kg/m2. Soit m la masse correspondante.
On a alors : 25 =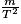 , soit : m = 25 × T2.
, soit : m = 25 × T2.
Or T2 ne varie pas (c'est la taille au carré) et vaut :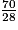 .
.
D'où : m = (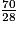 × 25) kg = 62,5 kg. Et 70 − 62,5 = 7,5.
× 25) kg = 62,5 kg. Et 70 − 62,5 = 7,5.
La personne doit perdre 7,5 kg.
IMC = 28 kg/m2 et M = 70 kg. On en déduit que : T2 =
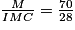 .
.On veut : IMC = 25 kg/m2. Soit m la masse correspondante.
On a alors : 25 =
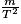 , soit : m = 25 × T2.
, soit : m = 25 × T2.Or T2 ne varie pas (c'est la taille au carré) et vaut :
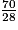 .
.D'où : m = (
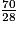 × 25) kg = 62,5 kg. Et 70 − 62,5 = 7,5.
× 25) kg = 62,5 kg. Et 70 − 62,5 = 7,5.La personne doit perdre 7,5 kg.
4. Encadrement de la masse d'une personne de 1,72 m ayant une corpulence « normale »
Soit x la masse minimale et y la masse maximale d'une personne ayant une corpulence « normale ».
On veut :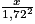 = 18,5, d'où x
= 18,5, d'où x  54,7 kg.
54,7 kg.
De même, on veut :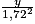 = 25, d'où y
= 25, d'où y  74 kg.
74 kg.
Pour avoir une corpulence « normale », une personne mesurant 1,72 m doit avoir une masse supérieure à 54,7 et strictement inférieure à 74 kg.
Soit x la masse minimale et y la masse maximale d'une personne ayant une corpulence « normale ».
On veut :
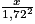 = 18,5, d'où x
= 18,5, d'où x  54,7 kg.
54,7 kg.De même, on veut :
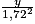 = 25, d'où y
= 25, d'où y  74 kg.
74 kg.Pour avoir une corpulence « normale », une personne mesurant 1,72 m doit avoir une masse supérieure à 54,7 et strictement inférieure à 74 kg.
B. L'obésité et le surpoids en France
1. Probabilité pour que la personne soit en surpoids ou obèse
La probabilité cherchée correspond au quotient :
(nb de personnes interrogées en surpoids ou obèses)/(nb total de personnes interrogées).
Soit :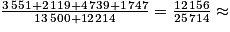 0,47.
0,47.
La probabilité que la personne interrogée soit en surpoids ou obèse est d'environ 47 %.
La probabilité cherchée correspond au quotient :
(nb de personnes interrogées en surpoids ou obèses)/(nb total de personnes interrogées).
Soit :
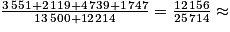 0,47.
0,47.La probabilité que la personne interrogée soit en surpoids ou obèse est d'environ 47 %.
2. Probabilité pour que l'homme soit en surpoids ou obèse
La probabilité cherchée correspond au quotient :
(nb d'hommes interrogés en surpoids ou obèses)/(nb total d'hommes interrogés).
Soit :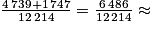 0,53.
0,53.
La probabilité que l'homme interrogé soit en surpoids ou obèse est d'environ 53 %.
La probabilité cherchée correspond au quotient :
(nb d'hommes interrogés en surpoids ou obèses)/(nb total d'hommes interrogés).
Soit :
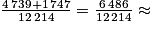 0,53.
0,53.La probabilité que l'homme interrogé soit en surpoids ou obèse est d'environ 53 %.
3. Probabilité pour que la personne obèse soit un homme
Il y a 2 119 + 1 747 = 3 866 personnes obèses parmi celles qui sont interrogées.
Parmi elles, 1 747 sont des hommes.
On a donc :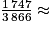 0,45.
0,45.
La probabilité pour que la personne obèse appelée soit un homme est donc d'environ 45 %.
Il y a 2 119 + 1 747 = 3 866 personnes obèses parmi celles qui sont interrogées.
Parmi elles, 1 747 sont des hommes.
On a donc :
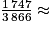 0,45.
0,45.La probabilité pour que la personne obèse appelée soit un homme est donc d'environ 45 %.
4. Vrai ou faux : 1/6 de l'échantillon est obèse
Il y a 3 866 personnes obèses, sur un total de 25 714 personnes. Les personnes obèses représentent donc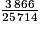 de la population. Or,
de la population. Or, 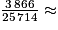 0,15 et
0,15 et 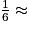 0,17 ; il y a donc moins d'un sixième de l'échantillon qui est obèse.
0,17 ; il y a donc moins d'un sixième de l'échantillon qui est obèse.
La personne a tort.
Il y a 3 866 personnes obèses, sur un total de 25 714 personnes. Les personnes obèses représentent donc
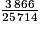 de la population. Or,
de la population. Or, 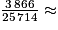 0,15 et
0,15 et 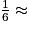 0,17 ; il y a donc moins d'un sixième de l'échantillon qui est obèse.
0,17 ; il y a donc moins d'un sixième de l'échantillon qui est obèse.La personne a tort.
C. Utilisation et interprétation de l'IMC chez l'enfant
1. Relation entre IMC et âge
Une relation de proportionnalité est représentée par une droite passant par l'origine.
Les courbes représentant l'IMC en fonction de l'âge ne sont pas des droites ; l'IMC n'est donc pas proportionnel à l'âge chez l'enfant.
Une relation de proportionnalité est représentée par une droite passant par l'origine.
Les courbes représentant l'IMC en fonction de l'âge ne sont pas des droites ; l'IMC n'est donc pas proportionnel à l'âge chez l'enfant.
2.
a) IMC maximum d'une fille de 12 ans sans surpoids
Une fille de 12 ans doit avoir un IMC maximum de 22 kg/m2 pour ne pas être considérée en surpoids.
Une fille de 12 ans doit avoir un IMC maximum de 22 kg/m2 pour ne pas être considérée en surpoids.
b) IMC maximum et minimum pour une corpulence normale à 7 ans
À 7 ans, une fille doit avoir un IMC compris entre 13 kg/m2 et 18 kg/m2 pour être considérée comme étant de corpulence normale.
À 7 ans, une fille doit avoir un IMC compris entre 13 kg/m2 et 18 kg/m2 pour être considérée comme étant de corpulence normale.
c) Âge à partir duquel une fille d'IMC 15 kg/m2 est considérée en insuffisance pondérale
Une fille d'IMC 15 kg/m2 est considérée en insuffisance pondérale à partir d'environ 13 ans et demi.
Une fille d'IMC 15 kg/m2 est considérée en insuffisance pondérale à partir d'environ 13 ans et demi.
3. Tranches d'âge sur lesquelles Emma avait un IMC inférieur ou égal à 16 kg/m2
Emma avait un IMC inférieur ou égal à 16 kg/m2 entre 0 et 6 mois et entre 2 ans et 10 ans.
Emma avait un IMC inférieur ou égal à 16 kg/m2 entre 0 et 6 mois et entre 2 ans et 10 ans.
D. Alimentation
1. Tableau complété
| Valeurs nutritionnelles moyennes pour le goûter de Frédéric | 1 portion de 30 g de gâteau | 200 mL de soda | Total |
|---|---|---|---|
| Matières grasses (lipides) dont acides gras saturés | 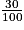 × 16 = 4,8 × 16 = 4,8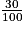 × 6,2 = 1,86 × 6,2 = 1,86 | 0 0 | 4,8 1,86 |
| Glucides dont sucres | 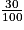 × 54 = 16,2 × 54 = 16,2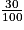 × 42 = 12,6 × 42 = 12,6 | 2 × 14,7 = 29,4 2 × 14,7 = 29,4 | 45,6 42 |
| Protéines | 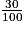 × 5,5 = 1,65 × 5,5 = 1,65 | 0 | 1,65 |
2.
a) Apport énergétique du sucre contenu dans le goûter de Frédéric
Le goûter de Frédéric contient 42 g de sucre. 6 g de sucre correspondent à un apport énergétique de 24 kcal.
42 = 7 × 6 et 7 × 24 = 168.
Le sucre contenu dans le goûter de Frédéric a un apport énergétique de 168 kcal.
Le goûter de Frédéric contient 42 g de sucre. 6 g de sucre correspondent à un apport énergétique de 24 kcal.
42 = 7 × 6 et 7 × 24 = 168.
Le sucre contenu dans le goûter de Frédéric a un apport énergétique de 168 kcal.
b) Consommation quotidienne maximale de sucre pour Frédéric
L'apport énergétique représenté par la consommation de sucre de Frédéric ne doit pas dépasser 0,1 × 1 985 kcal = 198,5 kcal.
Or, un morceau de sucre correspond à 24 kcal. On a : 198,5 ÷ 24 8,3.
8,3.
Frédéric ne devrait pas consommer plus de l'équivalent de 8 morceaux de sucre par jour.
L'apport énergétique représenté par la consommation de sucre de Frédéric ne doit pas dépasser 0,1 × 1 985 kcal = 198,5 kcal.
Or, un morceau de sucre correspond à 24 kcal. On a : 198,5 ÷ 24
 8,3.
8,3.Frédéric ne devrait pas consommer plus de l'équivalent de 8 morceaux de sucre par jour.
c) Pourcentage des AQR en sucre consommé par Frédéric au goûter
Frédéric consomme 168 kcal sous forme de sucre au goûter et les apports quotidiens recommandés sont de 1 985 kcal. On a :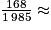 0,085.
0,085.
Le goûter de Frédéric représente un apport en sucre correspondant à environ 8,5 % des AQR.
Frédéric consomme 168 kcal sous forme de sucre au goûter et les apports quotidiens recommandés sont de 1 985 kcal. On a :
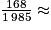 0,085.
0,085.Le goûter de Frédéric représente un apport en sucre correspondant à environ 8,5 % des AQR.
Deuxième partie
Exercice 1
1. Perpendicularité des droites (AB) et (BC)
Montrons que le triangle ABC est rectangle en B.
AC2 = 102 cm2 = 100 cm2.
AB2 + BC2 = (62 + 82) cm2 = (36 + 64) cm2 = 100 cm2.
On a donc : AC2 = AB2 + BC2. D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B. On en déduit que la droite (AB) est perpendiculaire à la droite (BC).
Montrons que le triangle ABC est rectangle en B.
AC2 = 102 cm2 = 100 cm2.
AB2 + BC2 = (62 + 82) cm2 = (36 + 64) cm2 = 100 cm2.
On a donc : AC2 = AB2 + BC2. D'après la réciproque du théorème de Pythagore, le triangle ABC est rectangle en B. On en déduit que la droite (AB) est perpendiculaire à la droite (BC).
Remarque
Dans la suite, comme l'énoncé n'indique pas le degré de précision d'éventuelles valeurs approchées, on donnera systématiquement les valeurs exactes des résultats.2. Calcul de la longueur BD
D étant par hypothèse sur le segment [BC], on sait que le triangle ABD est rectangle en B d'après la question précédente.
D'après le théorème de Pythagore, on a donc : AB2 + BD2 = AD2. D'où :
BD =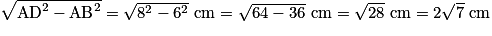 .
.
La longueur BD mesure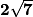 cm.
cm.
D étant par hypothèse sur le segment [BC], on sait que le triangle ABD est rectangle en B d'après la question précédente.
D'après le théorème de Pythagore, on a donc : AB2 + BD2 = AD2. D'où :
BD =
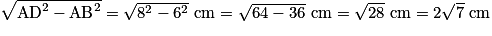 .
.La longueur BD mesure
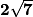 cm.
cm.3. Calcul de la longueur CE
Par hypothèse, (EC) est perpendiculaire à (BC) et, d'après la question 1., (AB) est perpendiculaire à (BC) ; les droites (AB) et (EC) sont donc parallèles.
Par ailleurs, les droites (BC) et (AE) sont sécantes en D.
D'après le théorème de Thalès, on a donc :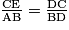 (1).
(1).
D étant sur [BC], BD = BC − BD = (8 −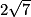 ) cm ; l'égalité (1) donne donc :
) cm ; l'égalité (1) donne donc :
CE = AB ×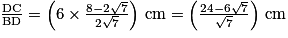 .
.
La longueur CE mesure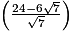 cm, soit environ 3,1 cm.
cm, soit environ 3,1 cm.
Par hypothèse, (EC) est perpendiculaire à (BC) et, d'après la question 1., (AB) est perpendiculaire à (BC) ; les droites (AB) et (EC) sont donc parallèles.
Par ailleurs, les droites (BC) et (AE) sont sécantes en D.
D'après le théorème de Thalès, on a donc :
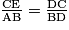 (1).
(1).D étant sur [BC], BD = BC − BD = (8 −
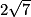 ) cm ; l'égalité (1) donne donc :
) cm ; l'égalité (1) donne donc :CE = AB ×
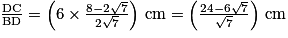 .
.La longueur CE mesure
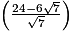 cm, soit environ 3,1 cm.
cm, soit environ 3,1 cm.4. Calcul de l'aire du triangle ACE
AireACE = AireABC − AireABD + AireDCE =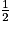 × AB × BC −
× AB × BC − 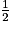 × AB × BD +
× AB × BD + 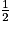 × DC × CE.
× DC × CE.
D'où : AireACE =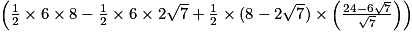 cm2.
cm2.
=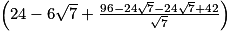 cm2.
cm2.
=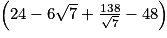 cm2.
cm2.
=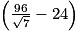 cm2.
cm2.
L'aire du triangle ACE mesure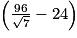 cm2, soit environ 12,28 cm2.
cm2, soit environ 12,28 cm2.
AireACE = AireABC − AireABD + AireDCE =
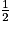 × AB × BC −
× AB × BC − 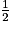 × AB × BD +
× AB × BD + 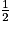 × DC × CE.
× DC × CE.D'où : AireACE =
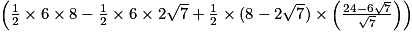 cm2.
cm2.=
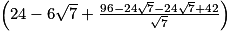 cm2.
cm2.=
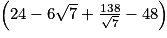 cm2.
cm2.=
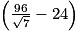 cm2.
cm2.L'aire du triangle ACE mesure
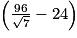 cm2, soit environ 12,28 cm2.
cm2, soit environ 12,28 cm2.Exercice 2
1. Divisibilité de 30n + 25 par 5
30n + 25 = 5(6n + 5)
Comme n est entier, 6n + 5 aussi, et 30n + 25 est donc, au vu de l'égalité ci-dessus, un multiple de 5.
30n + 25 est divisible par 5, pour tout entier n.
30n + 25 = 5(6n + 5)
Comme n est entier, 6n + 5 aussi, et 30n + 25 est donc, au vu de l'égalité ci-dessus, un multiple de 5.
30n + 25 est divisible par 5, pour tout entier n.
2.
a) Résultat obtenu si le nombre choisi est 8
Si le nombre choisi est 8, on obtient, successivement :
8 × 3 = 24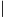 24 + 5 = 29
24 + 5 = 29  292 = 841
292 = 841
9 × 82 = 9 × 64 = 576
841 − 576 = 265
Si le nombre choisi est 8, on obtient 265.
Si le nombre choisi est 8, on obtient, successivement :
8 × 3 = 24
 24 + 5 = 29
24 + 5 = 29  292 = 841
292 = 8419 × 82 = 9 × 64 = 576
841 − 576 = 265
Si le nombre choisi est 8, on obtient 265.
b) Résultat obtenu si le nombre choisi est −56
Si le nombre choisi est −56, on obtient, successivement :
(−56) × 3 = −168 −168 + 5 = −163
−168 + 5 = −163  (−163)2 = 26 569
(−163)2 = 26 569
9 × (−56)2 = 28 224
26 569 − 28 224 = −1 655
Si le nombre choisi est −56, on obtient −1 655.
Si le nombre choisi est −56, on obtient, successivement :
(−56) × 3 = −168
 −168 + 5 = −163
−168 + 5 = −163  (−163)2 = 26 569
(−163)2 = 26 5699 × (−56)2 = 28 224
26 569 − 28 224 = −1 655
Si le nombre choisi est −56, on obtient −1 655.
c) Divisibilité du résultat par 5, quel que soit le nombre choisi
Soit n le nombre choisi.
En effectuant le programme, on obtient :
(3n + 5)2 − 9n2 = 9n2 + 30n + 25 − 9n2 = 30n + 25.
Or, d'après la question 1., 30n + 25 est toujours divisible par 5.
Quel que soit le nombre choisi, le résultat du programme est toujours divisible par 5.
Soit n le nombre choisi.
En effectuant le programme, on obtient :
(3n + 5)2 − 9n2 = 9n2 + 30n + 25 − 9n2 = 30n + 25.
Or, d'après la question 1., 30n + 25 est toujours divisible par 5.
Quel que soit le nombre choisi, le résultat du programme est toujours divisible par 5.
Exercice 3
1. Programme utilisé pour tracer le dessin
Le programme utilisé pour tracer le dessin est le programme C.
Le programme utilisé pour tracer le dessin est le programme C.
2. Justification de l'angle de rotation
Le dessin est constitué de triangles équilatéraux. Pour tracer un triangle équilatéral, il faut tracer des côtés adjacents faisant entre eux un angle de 60°. Le lutin étant orienté dans une direction donnée, si l'on veut que le tracé suivant fasse un angle de 60° avec la direction antérieure, il faut faire exécuter une rotation d'un angle supplémentaire à 60°, autrement dit, de mesure : 180° − 60° = 120°.
Le dessin est constitué de triangles équilatéraux. Pour tracer un triangle équilatéral, il faut tracer des côtés adjacents faisant entre eux un angle de 60°. Le lutin étant orienté dans une direction donnée, si l'on veut que le tracé suivant fasse un angle de 60° avec la direction antérieure, il faut faire exécuter une rotation d'un angle supplémentaire à 60°, autrement dit, de mesure : 180° − 60° = 120°.
3. Tracé à main levée des figures obtenues par les différents programmes
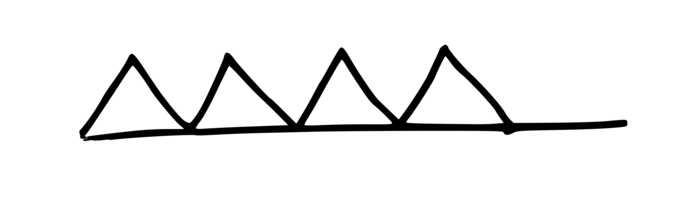 |
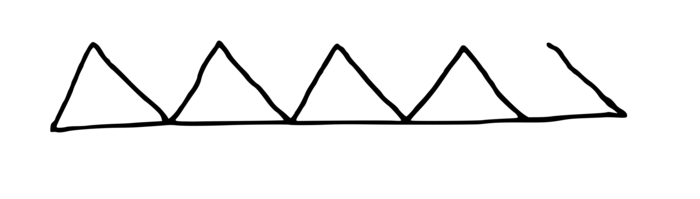 |
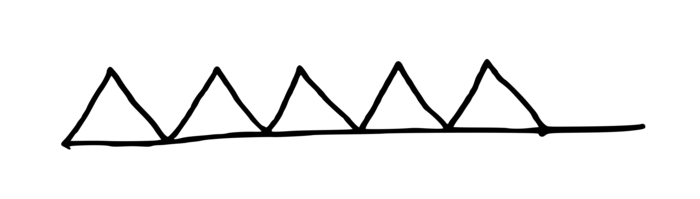 |
Troisième partie
Situation 1
1. Mobilisation des compétences « modéliser » et « calculer »
Remarque
En utilisant la typologie de Vergnaud, on peut dire que le problème posé est un problème additif de comparaison d'états, avec recherche du référent.Sans se référer à la typologie de Vergnaud, puisque ce n'est pas un objet d'enseignement explicite, les élèves doivent toutefois, pour résoudre le problème, soit le reconnaître comme étant d'un type déjà rencontré, soit s'en construire une représentation. Ils vont ensuite devoir développer une procédure de résolution, en lien avec la représentation du problème mobilisée.
Les élèves modélisent donc le problème : ils mettent en relation des informations textuelles avec un modèle mathématique (type de problème et procédure associée).
Bien que ce ne soit pas le seul type de procédure possible, l'objectif est ici le passage par le calcul pour résoudre le problème. Les élèves sont alors amenées à calculer (soit une différence soit une addition à trou) pour trouver la réponse attendue.
Les élèves modélisent donc le problème : ils mettent en relation des informations textuelles avec un modèle mathématique (type de problème et procédure associée).
Bien que ce ne soit pas le seul type de procédure possible, l'objectif est ici le passage par le calcul pour résoudre le problème. Les élèves sont alors amenées à calculer (soit une différence soit une addition à trou) pour trouver la réponse attendue.
2. Deux difficultés pouvant être rencontrées par les élèves
Remarque
On peut s'appuyer sur la question précédente pour répondre.Les élèves peuvent rencontrer des difficultés de modélisation du problème : l'expression « de plus » est ici un inducteur contre-intuitif et peut amener les élèves à modéliser le problème comme s'il s'agissait de la recherche du référé et donc opérer une addition des données 24 et 8.
Les élèves peuvent également rencontrer des difficultés de calcul en opérant mentalement 24 − 8.
Les élèves peuvent également rencontrer des difficultés de calcul en opérant mentalement 24 − 8.
3.
a) Analyse des quatre traces écrites
Remarque
Pour ce type de questions, il est recommandé de présenter la réponse à l'aide d'un tableau. La réponse gagne en lisibilité et la candidate ou le candidat s'assure qu'elle/il a bien abordé tous les aspects de la question…| Procédures suivies | Compétences mises en œuvre | Erreurs éventuelles | |
|---|---|---|---|
| Kiara | Kiara effectue en ligne l'addition 24 + 8. | Elle reconnaît un problème de type additif. Elle sait effectuer mentalement l'addition. | Elle se trompe dans la représentation du problème, qu'elle traite comme s'il s'agissait de la recherche du référé (autrement dit, comme si Lilou avait 8 euros de plus que Léo). Sa réponse est donc erronée. |
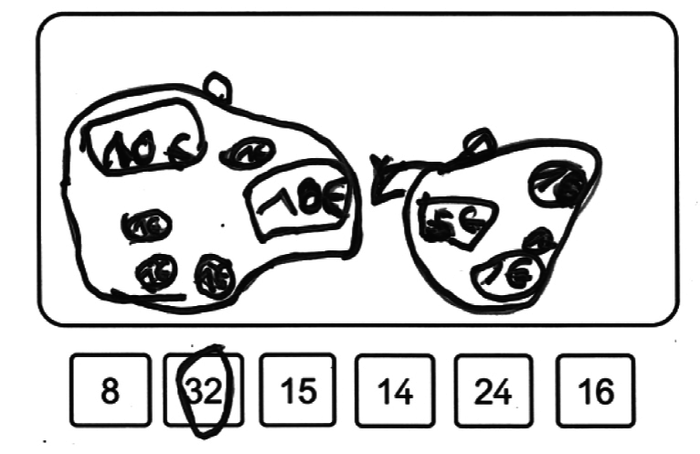
| Lucas | Lucas dessine, sous forme de billets de 10 € ou 5 € et de pièces de 1 €, la somme détenue par Léo et les 8 euros supplémentaires. Il totalise la somme représentée. | Il sait représenter, de façon réaliste, les sommes en jeu. Il sait additionner 10, 5 et 1 mentalement. | Il se trompe dans la représentation du problème, qu'il traite comme s'il s'agissait de la recherche du référé, voire qu'il réinterprète comme un problème de composition d'états avec recherche du tout (au vu de son dessin). Sa réponse est erronée. |
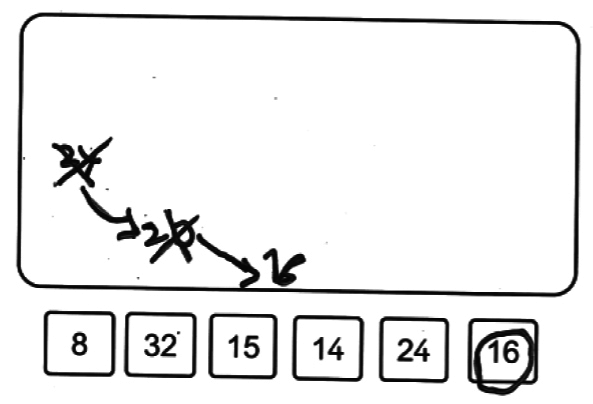
| Maya | Maya retranche 4 à 24, puis encore 4 au résultat obtenu, en écrivant les résultats intermédiaires et en matérialisant les retraits par des flèches. | Elle sait se représenter le problème. Elle sait décomposer mentalement 24 en 20 + 4, 8 en 4 + 4 et retrancher 4 à 20. | Pas d'erreur. |
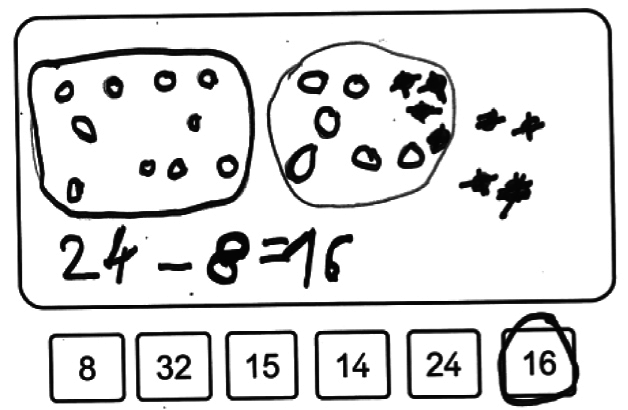
| Arif | Arif représente le nombre 24 en utilisant la constellation des dés. Il barre ensuite 8 points et traduit son action par le calcul en ligne : 24 − 8 = 16. | Il sait se représenter le problème et traduire sa procédure sous forme de calcul en ligne. On ne saurait toutefois affirmer ici qu'il sait calculer mentalement la différence, le résultat ayant pu être obtenu par décomptage des points sur la représentation dessinée. | Pas d'erreur. |
b) Remédiation ou accompagnement en direction de Lucas et Kiara
Il faut aider Lucas et Kiara à trouver le « bon » modèle. Cela peut passer par :
Il faut aider Lucas et Kiara à trouver le « bon » modèle. Cela peut passer par :
- un travail sur l'énoncé : reformulation, par l'enseignant, de l'expression « de plus », explicitation des liens entre les données, etc. ;
- une proposition de (ou un accompagnement vers la) schématisation ou de représentation ;
- l'utilisation de matériel de numération pour mettre en scène la situation.
4. Schéma possible pour représenter le problème
L'enseignant peut proposer le schéma suivant :
L'enseignant peut proposer le schéma suivant :
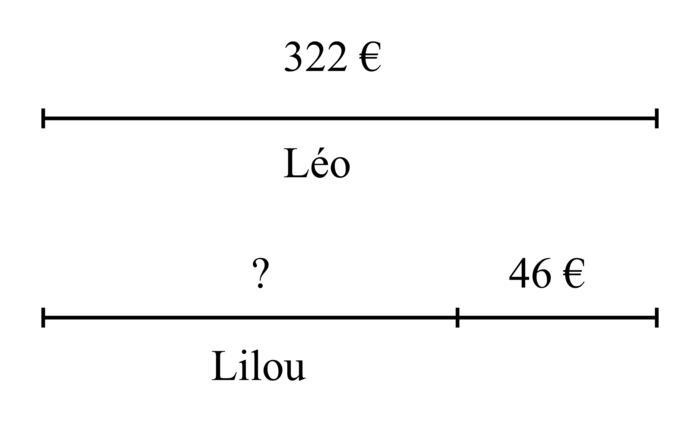 |
Situation 2
1. Justification du caractère erroné de la réponse de l'élève
Pour convaincre l'élève du caractère erroné de sa réponse, on peut lui faire observer qu'avec son raisonnement le petit côté du lit va mesurer 10 carreaux, que la longueur de l'étagère, qui est la même que le grand côté du lit, va mesurer 12 carreaux… et que 12 + 10 carreaux ne tiendront pas dans les 18 carreaux annoncés pour la longueur de la pièce (sans compter l'espace entre l'étagère et le lit !).
Pour convaincre l'élève du caractère erroné de sa réponse, on peut lui faire observer qu'avec son raisonnement le petit côté du lit va mesurer 10 carreaux, que la longueur de l'étagère, qui est la même que le grand côté du lit, va mesurer 12 carreaux… et que 12 + 10 carreaux ne tiendront pas dans les 18 carreaux annoncés pour la longueur de la pièce (sans compter l'espace entre l'étagère et le lit !).
2. Trois procédures correctes et propriétés mathématiques correspondantes
Toutes les procédures s'appuient sur la correspondance :
12 (dimension initiale) → 18 (dimension finale).
Toutes les procédures s'appuient sur la correspondance :
12 (dimension initiale) → 18 (dimension finale).
• 1re procédure, basée sur le coefficient de proportionnalité et donc sur la propriété d'égalité des rapports
L'élève observe que 18 = 12 × 1,5 puis multiplie successivement 6 et 2 par 1,5, pour trouver respectivement 9 et 3 (longueur et largeur de l'étagère).
L'élève observe que 18 = 12 × 1,5 puis multiplie successivement 6 et 2 par 1,5, pour trouver respectivement 9 et 3 (longueur et largeur de l'étagère).
• 2e procédure, basée sur la propriété de linéarité multiplicative
L'élève observe que 2 = 12 ÷ 6 et divise 18 par 6 pour obtenir 3. De même, il observe que 6 = 12 ÷ 2 et divise 18 par 2 pour obtenir 9.
L'élève observe que 2 = 12 ÷ 6 et divise 18 par 6 pour obtenir 3. De même, il observe que 6 = 12 ÷ 2 et divise 18 par 2 pour obtenir 9.
• 3e procédure, basée sur les propriétés de linéarité multiplicative et additive
L'élève observe que 2 = 12 ÷ 6 et divise 18 par 6 pour obtenir 3. Il observe ensuite que 6 = 2 + 2 + 2 et effectue donc 3 + 3 + 3 pour obtenir 9.
L'élève observe que 2 = 12 ÷ 6 et divise 18 par 6 pour obtenir 3. Il observe ensuite que 6 = 2 + 2 + 2 et effectue donc 3 + 3 + 3 pour obtenir 9.
Situation 3
1.
a) Réussites et erreurs des élèves à l'exercice 1
Célestine sait ranger des nombres entiers par ordre croissant. Toutefois, elle ne tient pas compte ici des virgules présentes dans les écritures décimales et range les nombres proposés (non entiers) comme s'il s'agissait d'entiers. Sa réponse est donc erronée.
Toufik se trompe de sens dans son rangement : il range les nombres proposés par ordre décroissant au lieu de croissant. Il sait toutefois ranger des nombres décimaux, même si sa réponse n'est pas celle attendue. Il ne connaît pas le sens de l'expression « par ordre croissant » et/ou du symbole « < ».
Paola ne commet pas d'erreur ; elle sait ranger des nombres décimaux par ordre croissant et connaît le sens de l'expression « par ordre croissant » et du symbole « < ».
Miroslav sait comparer des nombres entiers : il compare les parties entières des nombres proposés et en déduit que le nombre de partie entière « 6 » est supérieur à tous les autres, de parties entières égales à « 5 ».
Il sait également comparer les nombres entiers constitués des chiffres écrits à droite de la virgule, ce qui lui permet de proposer un rangement de tous les nombres de partie entière « 5 ». Sa représentation des nombres décimaux est toutefois erronée, puisqu'il les considère comme « deux nombres entiers séparés par une virgule ». Sa réponse est donc erronée.
Célestine sait ranger des nombres entiers par ordre croissant. Toutefois, elle ne tient pas compte ici des virgules présentes dans les écritures décimales et range les nombres proposés (non entiers) comme s'il s'agissait d'entiers. Sa réponse est donc erronée.
Toufik se trompe de sens dans son rangement : il range les nombres proposés par ordre décroissant au lieu de croissant. Il sait toutefois ranger des nombres décimaux, même si sa réponse n'est pas celle attendue. Il ne connaît pas le sens de l'expression « par ordre croissant » et/ou du symbole « < ».
Paola ne commet pas d'erreur ; elle sait ranger des nombres décimaux par ordre croissant et connaît le sens de l'expression « par ordre croissant » et du symbole « < ».
Miroslav sait comparer des nombres entiers : il compare les parties entières des nombres proposés et en déduit que le nombre de partie entière « 6 » est supérieur à tous les autres, de parties entières égales à « 5 ».
Il sait également comparer les nombres entiers constitués des chiffres écrits à droite de la virgule, ce qui lui permet de proposer un rangement de tous les nombres de partie entière « 5 ». Sa représentation des nombres décimaux est toutefois erronée, puisqu'il les considère comme « deux nombres entiers séparés par une virgule ». Sa réponse est donc erronée.
b) Tâche pouvant être proposée à Miroslav
L'enseignant pourrait proposer à Miroslav d'écrire les nombres à ranger sous forme de décompositions additives en entiers et fractions décimales, afin qu'il prenne conscience de la valeur positionnelle des chiffres de la partie décimale des nombres à ranger et du lien entre dixièmes, centièmes et millièmes.
L'enseignant pourrait proposer à Miroslav d'écrire les nombres à ranger sous forme de décompositions additives en entiers et fractions décimales, afin qu'il prenne conscience de la valeur positionnelle des chiffres de la partie décimale des nombres à ranger et du lien entre dixièmes, centièmes et millièmes.
2. Pertinence de l'exercice et proposition de modifications
Si l'on considère l'exercice proposé, la réponse attendue est :
7,01 < 7,32 < 7,35 < 7,57 < 12,05 < 12,42.
Or, Célestine, qui considérera les nombres 701, 732, 735, 757, 1 205 et 1 242 obtiendra le même rangement.
De même, Miroslav considérera que tous les nombres de partie entière « 7 » sont inférieurs à ceux de partie entière « 12 », puis comparera 01, 32, 35 et 57 d'une part, et 05 et 42 d'autre part, et obtiendra le rangement attendu.
L'exercice ne permettra donc pas de détecter les erreurs de procédure de Célestine et Miroslav.
Si l'on considère l'exercice proposé, la réponse attendue est :
7,01 < 7,32 < 7,35 < 7,57 < 12,05 < 12,42.
Or, Célestine, qui considérera les nombres 701, 732, 735, 757, 1 205 et 1 242 obtiendra le même rangement.
De même, Miroslav considérera que tous les nombres de partie entière « 7 » sont inférieurs à ceux de partie entière « 12 », puis comparera 01, 32, 35 et 57 d'une part, et 05 et 42 d'autre part, et obtiendra le rangement attendu.
L'exercice ne permettra donc pas de détecter les erreurs de procédure de Célestine et Miroslav.
On pourrait proposer de comparer les nombres suivants :
7,012 7,321 7,35 1,205 1,24.
Célestine répondra : 1,24 < 7,35 < 1,205 < 7,012 < 7,321.
Ou bien : 1,24 < 1,204 < 7,35 < 7,012 < 7,321 si elle fait un premier rangement selon la partie entière.
Miroslav, quant à lui, répondra : 1,205 < 1,24 < 7,012 < 7,35 < 7,321.
7,012 7,321 7,35 1,205 1,24.
Célestine répondra : 1,24 < 7,35 < 1,205 < 7,012 < 7,321.
Ou bien : 1,24 < 1,204 < 7,35 < 7,012 < 7,321 si elle fait un premier rangement selon la partie entière.
Miroslav, quant à lui, répondra : 1,205 < 1,24 < 7,012 < 7,35 < 7,321.
3. Analyse des réussites et erreurs de Célestine à l'exercice 2
Célestine répond correctement à la question a) car sa conception de la comparaison des nombres décimaux lui permet de dire qu'entre 83 et 85 il y a 84 ; elle répond donc « 8,4 », ce qui est une réponse valide.
Pour la question b), elle se sert sûrement d'expériences passées d'intercalage entre deux entiers successifs par la moyenne des deux nombres, ce qui lui fait considérer qu'entre 47 et 48, il y a 47,5 ; elle écrit donc « 4,7 », qu'elle complète par « 4,7,5 ».
Elle ne sait pas répondre à la question c), car les deux nombres entre lesquels il faut intercaler un nombre ne sont pas au même format, tout en ayant la même partie entière.
Célestine répond correctement à la question a) car sa conception de la comparaison des nombres décimaux lui permet de dire qu'entre 83 et 85 il y a 84 ; elle répond donc « 8,4 », ce qui est une réponse valide.
Pour la question b), elle se sert sûrement d'expériences passées d'intercalage entre deux entiers successifs par la moyenne des deux nombres, ce qui lui fait considérer qu'entre 47 et 48, il y a 47,5 ; elle écrit donc « 4,7 », qu'elle complète par « 4,7,5 ».
Elle ne sait pas répondre à la question c), car les deux nombres entre lesquels il faut intercaler un nombre ne sont pas au même format, tout en ayant la même partie entière.
Document précédent
Sujet 2019, groupement académique 2
