Dernier essai le
- Score :
/20
 |
Représentation d'une équation décrivant des phénomènes météorologiques imprévisibles (mouvements de l'atmosphère, l'écoulement de l'eau, etc.).
Équation a + x = b
a + x = b est une équation d'inconnue x.
La résoudre, c'est trouver le nombre que l'on peut écrire à la place de x de façon que l'égalité soit vraie ; ce nombre s'appelle la solution de l'équation.
La résoudre, c'est trouver le nombre que l'on peut écrire à la place de x de façon que l'égalité soit vraie ; ce nombre s'appelle la solution de l'équation.
Pour résoudre ce type d'équation, on utilise la règle suivante : on peut ajouter ou soustraire un même nombre aux deux membres d'une équation : on obtient alors une nouvelle équation qui a la même solution.
Exemple
On veut résoudre l'équation : 5,4 + x = 2.
On soustrait 5,4 aux deux membres de l'équation :
5,4 + x − 5,4 = 2 − 5,4
Puisque 5,4 − 5,4 = 0, on obtient : x = 2 − 5,4
Et finalement : x = −3,4.
L'équation 5,4 + x = 2 a pour solution le nombre −3,4.
On soustrait 5,4 aux deux membres de l'équation :
5,4 + x − 5,4 = 2 − 5,4
Puisque 5,4 − 5,4 = 0, on obtient : x = 2 − 5,4
Et finalement : x = −3,4.
L'équation 5,4 + x = 2 a pour solution le nombre −3,4.
Équation ax = b
ax = b est une équation d'inconnue x.
La résoudre, c'est trouver le nombre que l'on peut écrire à la place de x de façon que l'égalité soit vraie ; ce nombre s'appelle la solution de l'équation.
La résoudre, c'est trouver le nombre que l'on peut écrire à la place de x de façon que l'égalité soit vraie ; ce nombre s'appelle la solution de l'équation.
Pour résoudre ce type d'équation, on utilise la règle suivante : on peut multiplier ou diviser par un même nombre non nul les deux membres d'une équation : on obtient alors une nouvelle équation qui a la même solution.
Exemple
On veut résoudre l'équation : 3x = 7.
On divise les deux membres de l'équation par 3 :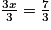 .
.
Puisque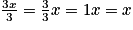 , l'équation ci-dessus s'écrit :
, l'équation ci-dessus s'écrit : 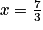 .
.
L'équation 3x = 7 a donc pour solution le nombre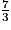 .
.
Vérifions l'égalité :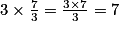 ; on a bien :
; on a bien : 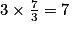 .
.
On divise les deux membres de l'équation par 3 :
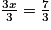 .
.Puisque
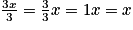 , l'équation ci-dessus s'écrit :
, l'équation ci-dessus s'écrit : 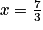 .
.L'équation 3x = 7 a donc pour solution le nombre
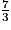 .
.Vérifions l'égalité :
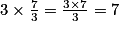 ; on a bien :
; on a bien : 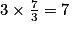 .
.Équation d'une droite
Dans un repère du plan, toute droite non parallèle à l'axe des ordonnées admet une équation de la forme : y = ax + b (a étant le coefficient directeur de la droite et b son ordonnée à l'origine).
Cette équation indique la relation existant entre les coordonnées x et y de n'importe quel point de la droite.
Cette équation indique la relation existant entre les coordonnées x et y de n'importe quel point de la droite.
Exemple
Prenons l'exemple de la droite D d'équation : y = −3x + 1.On peut dire que A(1 ; −2) est sur D car −2 = (−3) × 1 + 1.
Équation du premier degré à une inconnue
2x + 5 = x − 1 est une équation à une inconnue, x. La résoudre, c'est trouver la valeur numérique que l'on peut donner à x de façon que l'égalité soit vraie.
Cette équation est du premier degré car l'exposant de l'inconnue x est 1.
Cette équation est du premier degré car l'exposant de l'inconnue x est 1.
Règle
Pour résoudre ce type d'équation, on utilise les règles suivantes :- l'égalité est conservée quand on ajoute ou soustrait un même nombre aux deux membres d'une égalité ;
- l'égalité est conservée quand on multiplie ou divise par un même nombre non nul les deux membres d'une égalité.
Exemple
Résolvons l'équation 2x + 5 = x − 1.On ajoute à chaque membre de l'égalité − x et −5.
Après élimination des termes opposés, on obtient : 2x − x = −5 − 1.
D'où x = −6.
Équation produit
Une équation à une inconnue x est appelée équation produit si elle est de la forme A × B = 0, où A et B sont des facteurs du premier degré en x, c'est-à-dire de la forme ax + b (a et b étant des nombres donnés).
Règle
Pour résoudre une équation produit, on utilise la propriété suivante : si un produit de facteurs est nul, alors l'un au moins de ces facteurs est nul.On en déduit que A × B = 0 équivaut à A = 0 ou B = 0.
La résolution de A × B = 0 équivaut donc à la résolution de deux équations du premier degré en x : A = 0 ou B = 0.
Exemple
Résolvons l'équation (5x + 1) (2x − 4) = 0.Elle équivaut à :
5x + 1 = 0 ou 2x − 4 = 0
5x = − 1 ou 2x = 4
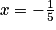 ou x = 2
ou x = 2L'équation a donc deux solutions :
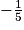 et 2.
et 2.
Document précédent
Les coordonnées
Document suivant
Les inéquations
