Enseignement Les épreuves du CRPE
Les inéquations
Imprimer
Dernier essai le - Score : /20
Inéquation du premier degré à une inconnue
Inéquation du premier degré à une inconnue
4x   −  1  supérieur ou égal  7x + 11 est une inéquation à une inconnue, x. La résoudre, c'est trouver toutes les valeurs numériques que l'on peut donner à x de façon que l'inégalité soit vraie.
Cette inéquation est du premier degré car l'exposant de l'inconnue x est 1.
Règle
Pour résoudre ce type d'inéquation, on utilise les propriétés des inégalités  :
  • l'ordre est conservé quand on ajoute ou soustrait un même nombre aux deux membres d'une inégalité ;
  • l'ordre est conservé quand on multiplie ou divise par un même nombre positif non nul les deux membres d'une inégalité ; il est inversé si le nombre est négatif.
Exemple
On veut résoudre l'inéquation 4x   −  1  supérieur ou égal  7x + 11.
Cette inéquation équivaut successivement à :
−3x   supérieur ou égal  12
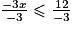\frac{-3x}{-3}\leq\frac{12}{-3} (on notera le changement de sens de l'inégalité)
x   inférieur ou égal   −4
Les solutions de l'inéquation sont tous les nombres inférieurs ou égaux à −4. On peut en donner une représentation graphique.