Enseignement Les épreuves du CRPE
La symétrie
Imprimer
Dernier essai le - Score : /20
Axe de symétrie

Axe de symétrie

Une droite  D est l'axe de symétrie d'une figure  F si et seulement si le symétrique par rapport à D de tout point M de la figure  F est aussi un point de  F .
Exemple
Dans un repère orthogonal, la courbe représentative d'une fonction paire admet l'axe des ordonnées comme axe de symétrie.
centre de symétrie

centre de symétrie

Un point I est le centre de symétrie d'une figure  F si et seulement si le symétrique par rapport à I de tout point M de la figure  F est aussi un point de  F.
Exemple
Dans un repère orthogonal, la courbe représentative d'une fonction impaire admet l'origine du repère comme centre de symétrie.
Médiatrice
La médiatrice d'un segment est la droite qui est perpendiculaire à ce segment et qui passe par son milieu.
   
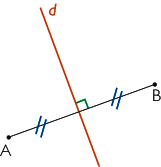 La médiatrice d'un segment est un axe de symétrie de ce segment.

Remarque
La médiatrice d'un segment est l'ensemble des points du plan qui sont équidistants des extrémités de ce segment.
   
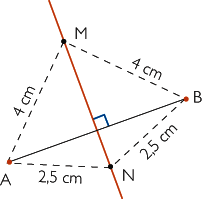 Si l'on considère un segment [AB], tout point de la médiatrice de [AB] est à la même distance de A et de B.
Par exemple, sur la figure ci-contre, le point M, qui appartient à la médiatrice de [AB], est situé à 4 cm de A et à 4 cm de B, le point N à 2,5 cm de A et à 2,5 cm de B.

Propriété de la symétrie
Propriété
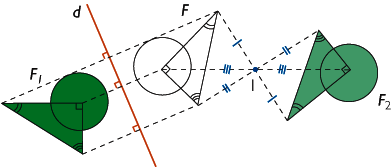
Dans une symétrie axiale ou une symétrie centrale  :
  • deux segments symétriques ont la même longueur (conservation des longueurs),
  • deux angles symétriques ont la même ouverture (conservation des angles),
  • deux figures symétriques ont la même aire (conservation des aires).
Exemple
Symétrie
La symétrie orthogonale d'axe   D est la transformation qui, à tout point M du plan, associe le point M' défini ainsi :
  • si M appartient à l'axe  D, alors M' = M ;
  • si M n'appartient pas à l'axe  D, alors D est la médiatrice du segment [MM'].
La symétrie de centre O est la transformation qui, à tout point M du plan associe le point M' défini ainsi :
  • si M = O, alors M' = M ;
  • si M est distinct de O, alors O est le milieu du segment [MM'].