Dernier essai le
- Score :
/20
Patron d'un cône de révolution
Exemple
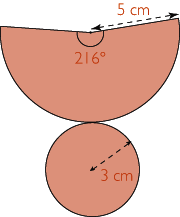
On veut construire un patron d'un cône de révolution dont le rayon de base mesure 3 cm et la hauteur, 4 cm. Le patron comprend :
- un disque de rayon 3 cm, qui représente la base,
- un secteur circulaire qui représente la surface latérale ; on peut calculer le rayon et l'angle de ce secteur circulaire à l'aide de la hauteur donnée.
 |
Patron d'un cylindre
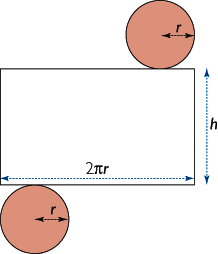
Le patron d'un cylindre est une surface plane composée de deux disques (les bases) et d'une surface rectangulaire. Il permet de reconstituer un cylindre par pliage.
 |
Patron d'un prisme droit
Le patron d'un prisme droit est une surface plane composée de deux surfaces polygonales (les bases) et de surfaces rectangulaires (les faces latérales). Il permet de reconstituer un prisme droit par pliage.
Exemple
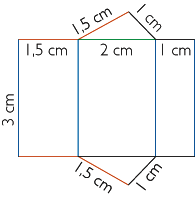
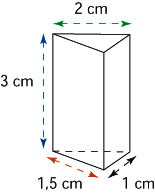
On veut construire le patron d'un prisme droit ayant les dimensions indiquées sur la représentation en perspective. Voici le schéma que l'on obtient :
 |
 |
Patron d'un solide
En pliant le patron d'un solide, on peut reconstituer ce solide.
Les arêtes qui se correspondent par pliage ont la même longueur.
Les arêtes qui se correspondent par pliage ont la même longueur.
Exemple
 |
| patron d'un cube |
| Un patron de cube est composé de six carrés superposables. |
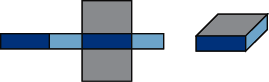 |
| patron d'un pavé droit |
| Un patron de pavé droit est composé de six rectangles superposables deux à deux. |
Patron d'une pyramide
Exemple
On veut construire un patron d'une pyramide régulière dont la base est un carré de côté 3 cm et dont chaque arête mesure 4 cm.
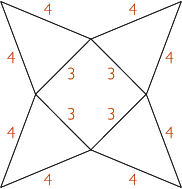 |
| Il suffit de dessiner un carré de côté 3 cm et quatre triangles isocèles dont un côté est un côté du carré et les deux autres mesurent 4 cm. |
Document précédent
La géométrie plane
Document suivant
La géométrie dans l'espace
