Dernier essai le
- Score :
/20
Sujet
Sujet
Le sujet est composé de cinq exercices indépendants : ci-dessous sont traités les exercices 3 et 4.
Exercice 3
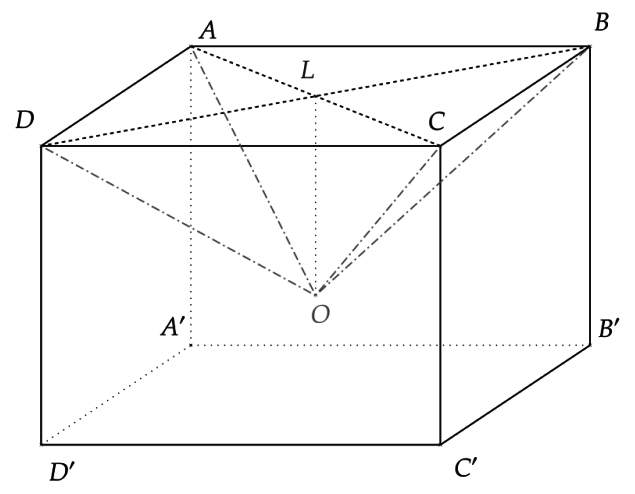
On considère un pavé droit ABCDA'B'C'D' avec DD' = 5 cm ; DC = 6 cm et DA = 7 cm.
On note L le point d'intersection des diagonales [AC] et [BD].
On souhaite creuser ce pavé, en retirant une pyramide OABCD de hauteur [OL].
On note L le point d'intersection des diagonales [AC] et [BD].
On souhaite creuser ce pavé, en retirant une pyramide OABCD de hauteur [OL].
 |
PARTIE A
Dans cette partie, on suppose que OL = 4 cm.
1. Montrer que AL  4,6 cm.
4,6 cm.
 4,6 cm.
4,6 cm.2. Construire le triangle ALO en vraie grandeur.
3.
a. Calculer le volume de la pyramide OABCD.
On rappelle que le volume d'une pyramide est égal au tiers du produit de l'aire de sa base par sa hauteur.
On rappelle que le volume d'une pyramide est égal au tiers du produit de l'aire de sa base par sa hauteur.
b. Calculer le volume du pavé creusé.
PARTIE B
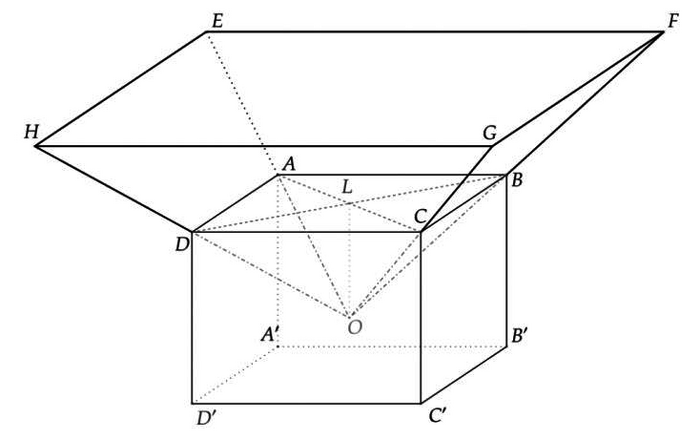
Dans cette partie, on pose OL = x, où x est un nombre compris entre 0 et 5. Le pavé creusé que l'on obtient est le socle en bois d'un trophée. Sur ce socle, on pose une pyramide en verre OEFGH qui est un agrandissement de la pyramide OABCD de rapport 2.
 |
1. Exprimer le volume de la pyramide OABCD en fonction de x.
2. Montrer que le volume du socle en bois est 210 − 14x.
3. Montrer que le volume de la pyramide en verre OEFGH est 112x.
4. Quelle valeur choisir pour x, pour que le volume de la pyramide en verre soit égal au double du volume du socle en bois ?
5. On considère les fonctions f et g définies pour tout x compris entre 0 et 5 par :
f(x) = 210 − 14x
et
g(x) =112x
f(x) = 210 − 14x
et
g(x) =112x
On a représenté dans un repère orthogonal ces deux fonctions.
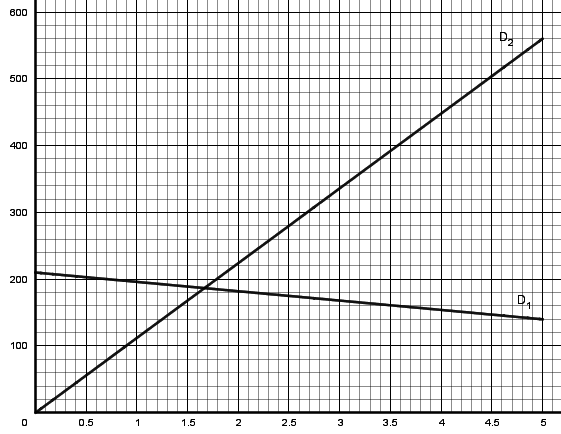 |
a. Déterminer quelle fonction (f ou g) est représentée par chacune des droites D1 et D2 ? Justifier.
b. Déterminer avec la précision permise par le graphique les valeurs de x pour lesquelles le volume du socle en bois est inférieur ou égal au volume de la pyramide en verre.
c. Retrouver le résultat précédent en posant puis en résolvant une inéquation.
Exercice 4
1.
Adam a réalisé le programme ci-contre à l'aide du logiciel Scratch.
 |
a. Montrer que si le nombre de départ est 3, le résultat est égal à 9.
b. Quel est le résultat donné par le programme si le nombre de départ est 2,4 ?
c. Soit x le nombre de départ. Montrer que le programme d'Adam retourne le nombre 2x2 − x − 6.
2.
Pauline propose le programme de calcul suivant.
Choisis un nombre.
Élève-le au carré
Soustrais 3.
Multiplie par 2.
Soustrais le nombre de départ.
Élève-le au carré
Soustrais 3.
Multiplie par 2.
Soustrais le nombre de départ.
a. Montrer que si le nombre de départ est 3, le résultat obtenu est égal à 9.
b. Quel est le résultat donné par le programme si le nombre de départ est 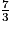 ?
?
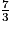 ?
?3. Montrer que, pour un même nombre de départ, les programmes de calcul d'Adam et Pauline donnent le même résultat.
4. Déterminer le ou les nombres de départ possibles pour que les résultats des programmes de calcul soient nuls. Justifier.
5. Adam souhaite automatiser les calculs de son programme pour les entiers naturels. Il utilise un tableur dont la copie d'écran est donnée ci-dessous. Quelle formule doit-il saisir dans la case B2 pour qu'il puisse l'étirer vers le bas sur l'ensemble de la colonne ?
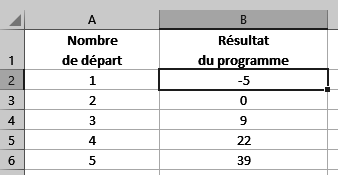 |
Corrigé
Corrigé
Exercice 3
PARTIE A
OL = 4 cm
1. ABCD est un rectangle par conséquent ADC est un triangle rectangle en B et d'après le théorème de Pythagore : AC2 = AD2+ DC2 = 72 + 62 = 85 d'où AC = 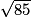 cm.
cm.
Puisque ABCD est un rectangle de centre L, L est le milieu de [AC] d'où
AL =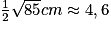 cm
cm
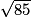 cm.
cm.Puisque ABCD est un rectangle de centre L, L est le milieu de [AC] d'où
AL =
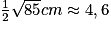 cm
cm2. Pour construire exactement le triangle ALO, on peut commencer par construire un rectangle A'B'C'D' de centre L de dimension 6 cm × 7 cm, puis à partir de ce triangle, reporter la longueur A'L' = AL et continuer la construction du triangle ALO rectangle en L, puisque OABCD est une pyramide de hauteur [OL].
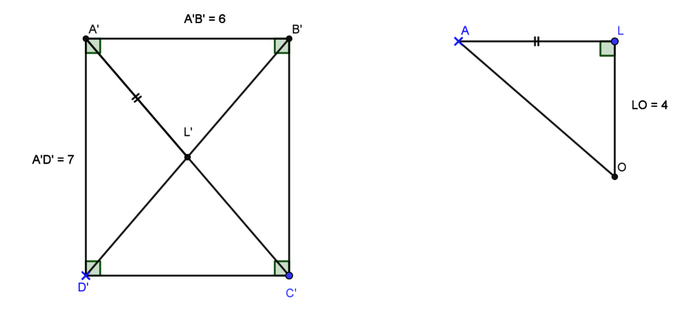 |
Remarque : on pouvait aussi partir de la valeur approchée de AL obtenue dans la question précédente mais la construction est moins précise.
3.
a. VOABCD = 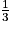 × (DA × DC) × OL =
× (DA × DC) × OL = 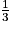 × 7 cm × 6 cm × 4 cm = 56 cm3
× 7 cm × 6 cm × 4 cm = 56 cm3
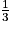 × (DA × DC) × OL =
× (DA × DC) × OL = 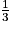 × 7 cm × 6 cm × 4 cm = 56 cm3
× 7 cm × 6 cm × 4 cm = 56 cm3b. Vpavé creusé = VABCD − VOABCD = 7 cm × 6 cm × 5 cm − 56 cm3 =
210 cm3 − 56 cm3 = 154 cm3
210 cm3 − 56 cm3 = 154 cm3
PARTIE B
L'unité de longueur implicite est le cm.
1. VOABCD = 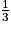 × (DA × DC) × OL =
× (DA × DC) × OL = 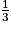 × 7 × 6 × x = 14x
× 7 × 6 × x = 14x
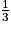 × (DA × DC) × OL =
× (DA × DC) × OL = 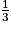 × 7 × 6 × x = 14x
× 7 × 6 × x = 14x2. Vsocle en bois = Vpavé creusé = VABCD − VOABCD = 210 − 14x
3. On sait qu'au cours d'un agrandissement de rapport k, les longueurs sont multipliées par k, les aires par k2 et les volumes par k3. La pyramide en verre OEFGH est un agrandissement de la pyramide OABCD de rapport k = 2 par conséquent
VOEFGH = k3 × VOABCD = 8 × 14x = 112x
VOEFGH = k3 × VOABCD = 8 × 14x = 112x
4. VOEFGH = 2 × Vsocle en bois  112x = 2(210 − 14x)
112x = 2(210 − 14x)  112x = 420 − 28x
112x = 420 − 28x
 140x = 420
140x = 420  x =
x = 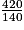
 x = 3
x = 3
Il faut choisir 3 cm comme hauteur de la pyramide OABCD pour que le volume de la pyramide en verre soit égal au double du volume du socle en bois.
 112x = 2(210 − 14x)
112x = 2(210 − 14x)  112x = 420 − 28x
112x = 420 − 28x 140x = 420
140x = 420  x =
x = 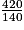
 x = 3
x = 3Il faut choisir 3 cm comme hauteur de la pyramide OABCD pour que le volume de la pyramide en verre soit égal au double du volume du socle en bois.
5.
a. La fonction g: x 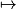 112x est une fonction linéaire donc sa représentation graphique est la droite D2 passant par l'origine du repère.
112x est une fonction linéaire donc sa représentation graphique est la droite D2 passant par l'origine du repère.
La fonction f: x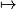 −14x + 210 est une fonction affine décroissante dont la représentation graphique est la droite D1 passant par le point de coordonnées (0 ; 210).
−14x + 210 est une fonction affine décroissante dont la représentation graphique est la droite D1 passant par le point de coordonnées (0 ; 210).
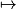 112x est une fonction linéaire donc sa représentation graphique est la droite D2 passant par l'origine du repère.
112x est une fonction linéaire donc sa représentation graphique est la droite D2 passant par l'origine du repère.La fonction f: x
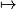 −14x + 210 est une fonction affine décroissante dont la représentation graphique est la droite D1 passant par le point de coordonnées (0 ; 210).
−14x + 210 est une fonction affine décroissante dont la représentation graphique est la droite D1 passant par le point de coordonnées (0 ; 210).b. Le volume du socle en bois s'exprime en fonction de x par f(x) et celui de la pyramide de verre par g(x). On détermine graphiquement les valeurs de x pour lesquelles f(x) g(x), ce qui se produit lorsque x est compris entre 1,7 environ et 5 (hauteur du pavé droit).
 |
c. -->
Le volume du socle en bois est inférieur ou égal au volume de la pyramide en verre si x est supérieur ou égal à 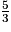 .
.
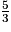 .
.Exercice 4
1.
Voici le programme en couleur pour mieux se repérer.
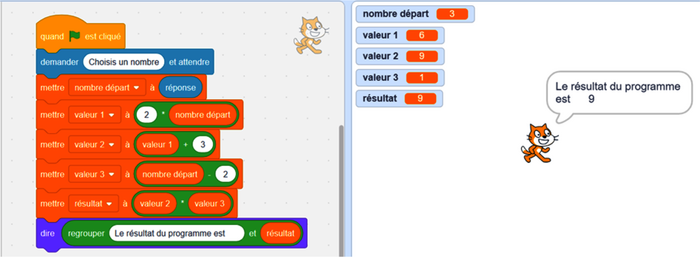 |
a. Si le nombre départ est 3, alors
– la valeur 1 est 2 × 3 = 6
– la valeur 2 est 6 + 3 = 9
– la valeur 3 est 3 − 2 = 1
– le résultat est 9 × 1 = 9
– la valeur 1 est 2 × 3 = 6
– la valeur 2 est 6 + 3 = 9
– la valeur 3 est 3 − 2 = 1
– le résultat est 9 × 1 = 9
b. Si le nombre départ est 2,4, alors
– la valeur 1 est 2 × 2,4 = 4,8
– la valeur 2 est 4,8 + 3 = 7,8
– la valeur 3 est 2,4 − 2 = 0,4
– le résultat est 7,8 × 0,4 = 3,12
– la valeur 1 est 2 × 2,4 = 4,8
– la valeur 2 est 4,8 + 3 = 7,8
– la valeur 3 est 2,4 − 2 = 0,4
– le résultat est 7,8 × 0,4 = 3,12
c. Si le nombre départ est x, alors
– la valeur 1 est 2 × x = 2x
– la valeur 2 est 2x + 3
– la valeur 3 est x − 2
– le résultat est (2x + 3)(x − 2) = 2x × x − 2x × 2 + 3 × x − 3 × 2
= 2x2 − 4x + 3x − 6
= 2x2 − x − 6
– la valeur 1 est 2 × x = 2x
– la valeur 2 est 2x + 3
– la valeur 3 est x − 2
– le résultat est (2x + 3)(x − 2) = 2x × x − 2x × 2 + 3 × x − 3 × 2
= 2x2 − 4x + 3x − 6
= 2x2 − x − 6
2.
a. Si le nombre départ du programme de Pauline est 3, alors
– en l'élevant au carré, on trouve 32 = 9
– en soustrayant 3 au résultat précédent, on trouve 9 − 3 = 6
– en multipliant par 2 le résultat précédent, on trouve 2 × 6 = 12
– en soustrayant le nombre de départ au résultat précédent, on trouve 12 − 3 = 9
– en l'élevant au carré, on trouve 32 = 9
– en soustrayant 3 au résultat précédent, on trouve 9 − 3 = 6
– en multipliant par 2 le résultat précédent, on trouve 2 × 6 = 12
– en soustrayant le nombre de départ au résultat précédent, on trouve 12 − 3 = 9
b. Si le nombre départ du programme de Pauline est 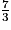 , alors
, alors
– en l'élevant au carré, on trouve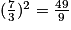
– en soustrayant 3 au résultat précédent, on trouve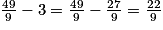
– en multipliant par 2 le résultat précédent, on trouve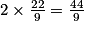
– en soustrayant le nombre de départ au résultat précédent , on trouve
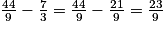
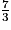 , alors
, alors– en l'élevant au carré, on trouve
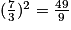
– en soustrayant 3 au résultat précédent, on trouve
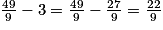
– en multipliant par 2 le résultat précédent, on trouve
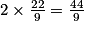
– en soustrayant le nombre de départ au résultat précédent , on trouve
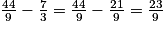
3. Si le nombre départ du programme de Pauline est x alors
– en l'élevant au carré, on trouve x2
– en soustrayant 3 au résultat précédent, on trouve x2 − 3
– en multipliant par 2 le résultat précédent, on trouve 2 × (x2 − 3) = 2x2 − 6
– en soustrayant le nombre de départ au résultat précédent , on trouve 2x2 − x − 3 soit la même expression qu'avec le programme d'Adam, et ce quelle que soit la valeur de x.
– en l'élevant au carré, on trouve x2
– en soustrayant 3 au résultat précédent, on trouve x2 − 3
– en multipliant par 2 le résultat précédent, on trouve 2 × (x2 − 3) = 2x2 − 6
– en soustrayant le nombre de départ au résultat précédent , on trouve 2x2 − x − 3 soit la même expression qu'avec le programme d'Adam, et ce quelle que soit la valeur de x.
4. Déterminer les valeurs de nombres x de départ qui donnent un résultat nul avec l'un ou l'autre programme revient à résoudre l'équation (2x + 3)(x − 2) = 0.
Un produit de facteurs est nul si et seulement si l'un au moins des facteurs est nul :
(2x + 3)(x − 2) = 0 2x + 3 = 0 ou x − 2 = 0
2x + 3 = 0 ou x − 2 = 0  x =
x = 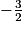 ou x = 2
ou x = 2
Un produit de facteurs est nul si et seulement si l'un au moins des facteurs est nul :
(2x + 3)(x − 2) = 0
 2x + 3 = 0 ou x − 2 = 0
2x + 3 = 0 ou x − 2 = 0  x =
x = 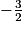 ou x = 2
ou x = 2Les nombres de départ qui annulent le résultat des programmes sont 2 et −1,5.
5. Adam peut saisir comme formule : = A*A2*A2 − A2 − 3
Document précédent
Sujet 2023 de mathématiques, groupement académique 3
