Enseignement Les épreuves du CRPE
Le théorème du cercle circonscrit
Imprimer
Dernier essai le - Score : /20
Théorème du cercle circonscrit à un triangle rectangle
Théorème du cercle circonscrit à un triangle rectangle
Propriété
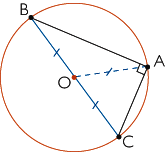Dans un triangle rectangle, le milieu de l'hypoténuse est le centre du cercle circonscrit à ce triangle.

Autres formulations du théorème :
  • Si un triangle est rectangle, alors il peut être inscrit dans un cercle ayant pour diamètre son hypoténuse.
  • Le milieu de l'hypoténuse d'un triangle rectangle est équidistant des trois sommets.
Réciproque
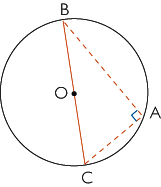Ce théorème admet une réciproque  : si le cercle circonscrit à un triangle ABC a pour diamètre le côté [BC], alors le triangle ABC est rectangle en A.