Dernier essai le
- Score :
/20
Aire
Donner l'aire d'une surface, c'est indiquer sa grandeur, son étendue.
Une aire s'exprime par un nombre suivi d'une unité d'aire.
Une aire s'exprime par un nombre suivi d'une unité d'aire.
Exemple
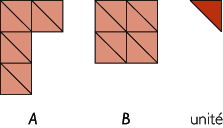
Prenons pour unité d'aire le triangle rouge ci-dessous.
Pour recouvrir la surface A, on a besoin de 8 triangles unités.
Pour recouvrir la surface B, on a besoin également de 8 triangles unités.
Dans l'unité choisie, l'aire des deux figures A et B est donc 8.
Pour recouvrir la surface A, on a besoin de 8 triangles unités.
Pour recouvrir la surface B, on a besoin également de 8 triangles unités.
Dans l'unité choisie, l'aire des deux figures A et B est donc 8.
 |
Remarque
Les unités d'aire du système métrique sont le mètre carré (m2), ses multiples et ses sous-multiples.
Pour passer de l'une à l'autre, il faut multiplier par 100 pour obtenir l'unité immédiatement supérieure et diviser par 100 pour obtenir l'unité immédiatement inférieure.
Pour passer de l'une à l'autre, il faut multiplier par 100 pour obtenir l'unité immédiatement supérieure et diviser par 100 pour obtenir l'unité immédiatement inférieure.
Grandeur produit
Les grandeurs produits sont des produits de grandeurs simples. L'unité de la grandeur produit dépend des unités dans lesquelles sont exprimées ces grandeurs simples.
Exemple
Les aires et les volumes sont des grandeurs produits : une aire est le produit de deux longueurs (exprimées dans la même unité) et un volume est le produit de trois longueurs (exprimées dans la même unité).
Pour mesurer le trafic d'une ligne de transport de marchandises, on utilise une grandeur produit : masse transportée × longueur du trajet.
Volume
Donner le volume d'un solide, c'est indiquer sa grandeur, l'espace qu'il occupe.
Un volume s'exprime par un nombre suivi d'une unité de volume.
Un volume s'exprime par un nombre suivi d'une unité de volume.
Exemple
 |
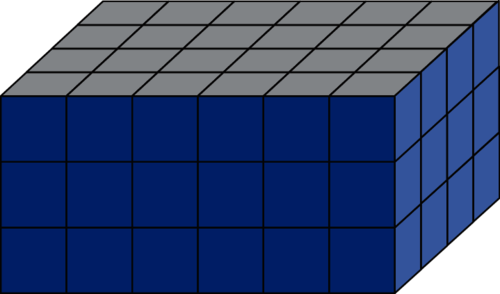
| Prenons pour unité de volume ce cube. |
Pour remplir le solide représenté ci-dessous, il faut 6 × 4 × 3, soit 72 cubes unités.
Dans l'unité choisie, le volume du solide est donc 72.
Dans l'unité choisie, le volume du solide est donc 72.
 |
Remarque
Les unités de volume du système métrique sont le mètre cube (m3), ses multiples et ses sous-multiples. Pour passer de l'une à l'autre, il faut multiplier par 1 000 pour obtenir l'unité immédiatement supérieure et diviser par 1 000 pour obtenir l'unité immédiatement inférieure.
On utilise couramment une autre unité, le litre (L) : 1 L = 1 dm3.
On utilise couramment une autre unité, le litre (L) : 1 L = 1 dm3.
Document précédent
Les échelles
Document suivant
Les grandeurs quotients
