Dernier essai le
- Score :
/20
Développer une expression
Développer une expression consiste à transformer un produit en une somme algébrique. On utilise la propriété de la distributivité de la multiplication par rapport à l'addition ou à la soustraction.
k (a + b) = k a + k b
k (a − b) = k a − k b
k (a + b) = k a + k b
k (a − b) = k a − k b
Exemple
Le produit contient une seule paire de parenthèses : A = a(a − 7) = a2 − 7a
Le produit contient deux paires de parenthèses ; on applique alors la propriété de la double distributivité :
B = (−5 + 3y)(y − 2)
B = −5y + 10 + 3y2 − 6y
B= 3y2 - 11y + 10
B = (−5 + 3y)(y − 2)
B = −5y + 10 + 3y2 − 6y
B= 3y2 - 11y + 10
Remarque
On peut aussi développer des expressions en utilisant les identités remarquables.
Factoriser une expression
Factoriser une expression consiste à transformer une somme algébrique en un produit.
Par exemple, quand on écrit : k a + k b = k (a + b) ou k a − k b = k (a − b), on a factorisé les expressions ka + kb et ka − kb.
Dans les deux cas, on dit qu'on a mis k en facteur. Le nombre k est appelé un facteur commun.
Ce facteur commun peut être un nombre, une lettre, le produit d'un nombre par une lettre ou une expression entre parenthèses.
Par exemple, quand on écrit : k a + k b = k (a + b) ou k a − k b = k (a − b), on a factorisé les expressions ka + kb et ka − kb.
Dans les deux cas, on dit qu'on a mis k en facteur. Le nombre k est appelé un facteur commun.
Ce facteur commun peut être un nombre, une lettre, le produit d'un nombre par une lettre ou une expression entre parenthèses.
Exemple
B = (2x + 3)(4x − 3) − (4x + 6)(7x + 8) B = (2x + 3)(4x − 3) − 2(2x + 3)(7x + 8) ; on a « fait apparaître » le facteur commun (2x + 3). B = (2x + 3)[(4x − 3) − 2(7x + 8)] ; on peut réduire l'expression trouvée et écrire : B = (2x + 3)(4x - 3 - 14x - 16) = (2x + 3)(-10x - 19).
Remarque
On peut aussi factoriser des expressions en utilisant les identités remarquables.
Réduction au même dénominateur
Règle
Soit deux nombres en écriture fractionnaire. Les réduire au même dénominateur revient à remplacer l'un des deux nombres (ou chacun des deux nombres) par un nombre égal, de façon qu'ils aient le même dénominateur. Pour remplacer un nombre par un autre, on utilise la règle suivante : 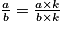 (b et k étant différents de 0).
(b et k étant différents de 0).
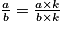 (b et k étant différents de 0).
(b et k étant différents de 0).Exemple
On veut réduire au même dénominateur 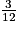 et
et 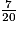 . Il s'agit donc de trouver un multiple de 12 qui soit également un multiple de 20 et de préférence le plus petit possible. Dans le tableau qui suit, on écrit, sur la première ligne, les premiers multiples de 12 et, sur la seconde, les premiers multiples de 20 jusqu'à ce que l'on ait le même nombre.
. Il s'agit donc de trouver un multiple de 12 qui soit également un multiple de 20 et de préférence le plus petit possible. Dans le tableau qui suit, on écrit, sur la première ligne, les premiers multiples de 12 et, sur la seconde, les premiers multiples de 20 jusqu'à ce que l'on ait le même nombre.
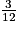 et
et 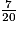 . Il s'agit donc de trouver un multiple de 12 qui soit également un multiple de 20 et de préférence le plus petit possible. Dans le tableau qui suit, on écrit, sur la première ligne, les premiers multiples de 12 et, sur la seconde, les premiers multiples de 20 jusqu'à ce que l'on ait le même nombre.
. Il s'agit donc de trouver un multiple de 12 qui soit également un multiple de 20 et de préférence le plus petit possible. Dans le tableau qui suit, on écrit, sur la première ligne, les premiers multiples de 12 et, sur la seconde, les premiers multiples de 20 jusqu'à ce que l'on ait le même nombre.| 12 | 24 | 36 | 48 | 60 |
| 20 | 40 | 60 | | |
60 est à la fois un multiple de 12 (60 = 5 × 12) et de 20 (60 = 20 × 3). On peut écrire : 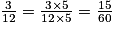 et
et 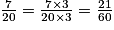 .
.
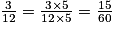 et
et 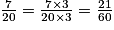 .
.Remarque
Dans l'exemple qui précède, 60 est le plus petit multiple commun non nul de 12 et de 20. On écrit ppcm (12 ; 20) = 60.
Les deux fractions étant réduites au même dénominateur 60, on peut alors les additionner ou les soustraire.
Réduire une expression littérale
Réduire une expression littérale (en l'occurrence une somme), c'est regrouper les termes semblables de façon à éviter leur répétition.
Exemple
Par exemple, réduire une somme écrite en fonction de x 2 et de x, c'est l'écrire sous la forme ax 2 + bx + c. Ainsi, si l'on veut réduire l'expression A = 3 − 5x 2 + 4x + 7x 2 − 12 − 4x :
- on regroupe les termes « en x 2 », ceux en « x » et les termes « sans x » ;
- on effectue les calculs qui peuvent l'être et on obtient : A = 2x 2 − 9.
Remarque
En réduisant une somme, on est amené à appliquer la propriété de distributivité de la multiplication : k × a + k × b = k × (a + b).
Simplifier une expression littérale
Pour alléger l'écriture d'un calcul littéral, on supprime le signe opératoire ×.
Exemples
3 × a et a × 3 peuvent s'écrire 3a. 3 × (a − 2) et (a − 2) × 3 peuvent s'écrire 3(a − 2). a × b et b × a peuvent s'écrire ab.
Simplifier une fraction
Règle
Simplifier une fraction revient à diviser le numérateur et le dénominateur par un même entier strictement positif (cet entier est donc un diviseur commun au numérateur et au dénominateur). La fraction obtenue est irréductible si elle ne peut plus être simplifiée.
Exemple
On veut écrire plus simplement 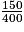 .
.
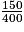 .
.On remarque que 150 et 400 sont des multiples de 10. On peut donc écrire : 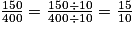 . On dit qu'on a simplifié la fraction
. On dit qu'on a simplifié la fraction 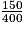 par 10.
par 10.
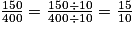 . On dit qu'on a simplifié la fraction
. On dit qu'on a simplifié la fraction 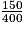 par 10.
par 10.On voit maintenant que 15 et 40 sont des multiples de 5. On a donc : 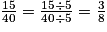 . On dit qu'on a simplifié la fraction
. On dit qu'on a simplifié la fraction 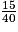 par 5.
par 5.
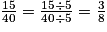 . On dit qu'on a simplifié la fraction
. On dit qu'on a simplifié la fraction 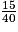 par 5.
par 5.Finalement, on peut écrire : 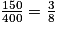 . Cette écriture ne peut plus être simplifiée. On dit qu'elle est irréductible.
. Cette écriture ne peut plus être simplifiée. On dit qu'elle est irréductible.
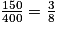 . Cette écriture ne peut plus être simplifiée. On dit qu'elle est irréductible.
. Cette écriture ne peut plus être simplifiée. On dit qu'elle est irréductible.
Document précédent
Les priorités opératoires
Document suivant
Les calculs sur des nombres en écriture fractionnaire
