Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
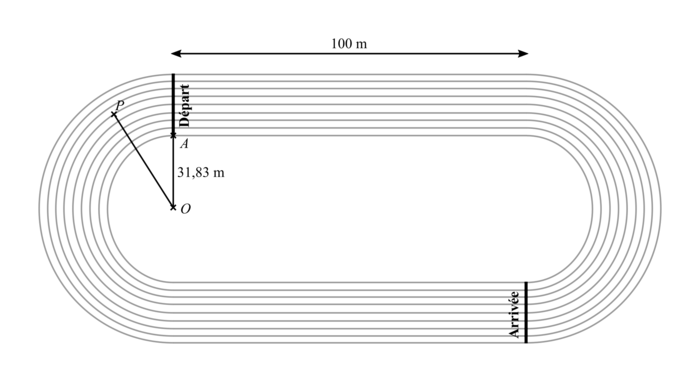
Une piste d'athlétisme est formée de huit couloirs. La largeur de chaque couloir est de 1,22 mètre. Chacun des neuf bords des huit couloirs est composé de deux lignes droites de 100 mètres et de deux demi-cercles. Le couloir 1 est celui le plus à l'intérieur, le 8 étant celui le plus à l'extérieur. Le bord intérieur du couloir 1 est composé de deux lignes droites de 100 mètres et de deux demi-cercles de rayon 31,83 mètres.
Dans tout l'exercice, on négligera la largeur des bandes de peinture délimitant les couloirs. Pour les courses de sprint (100 m, 200 m ou 400 m), il y a huit coureurs et chacun occupe un couloir.
Un coureur devant rester dans son couloir tout au long de la course, on considère que la distance qu'il parcourt est celle correspondant à la ligne la plus intérieure de son couloir.
Dans tout l'exercice, on négligera la largeur des bandes de peinture délimitant les couloirs. Pour les courses de sprint (100 m, 200 m ou 400 m), il y a huit coureurs et chacun occupe un couloir.
Un coureur devant rester dans son couloir tout au long de la course, on considère que la distance qu'il parcourt est celle correspondant à la ligne la plus intérieure de son couloir.
 |
1. Vérifier que la distance d'un tour de piste complet parcourue par le coureur du couloir 1 est d'environ 400 m.
2. Dessiner le couloir n° 1 (avec ses deux bords) à l'échelle 1/1 200. Indiquer les calculs effectués pour réaliser la construction.
On étudie dans les questions ci-dessous la configuration d'une course de 200 m.
3.
Expliquer pourquoi il y a un décalage au départ d'une course de 200 m comme sur la photographie ci-dessous.
 |
4.
Sur la représentation précédente :
- le point A correspond à la position de départ du coureur dans le couloir 1 ;
- le point P correspond à la position de départ du coureur dans le couloir 6. Pour ce coureur, le décalage correspond à la longueur de l'arc de cercle de centre O et qui a pour extrémités le point P et le point de la ligne 6 situé sur la ligne « Départ ».
a) Calculer le décalage du coureur du couloir 6 au centimètre près.
On peut repérer la position de départ dans le couloir par l'angle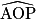 que l'on appelle α. Cet angle dépend du numéro n du couloir.
que l'on appelle α. Cet angle dépend du numéro n du couloir.
On peut repérer la position de départ dans le couloir par l'angle
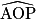 que l'on appelle α. Cet angle dépend du numéro n du couloir.
que l'on appelle α. Cet angle dépend du numéro n du couloir.b) Calculer la mesure de l'angle α pour le couloir n° 6. On donnera la mesure de l'angle arrondie au dixième de degré.
Voici la courbe d'une fonction permettant de déterminer la valeur de α en fonction du couloir n.
Voici la courbe d'une fonction permettant de déterminer la valeur de α en fonction du couloir n.
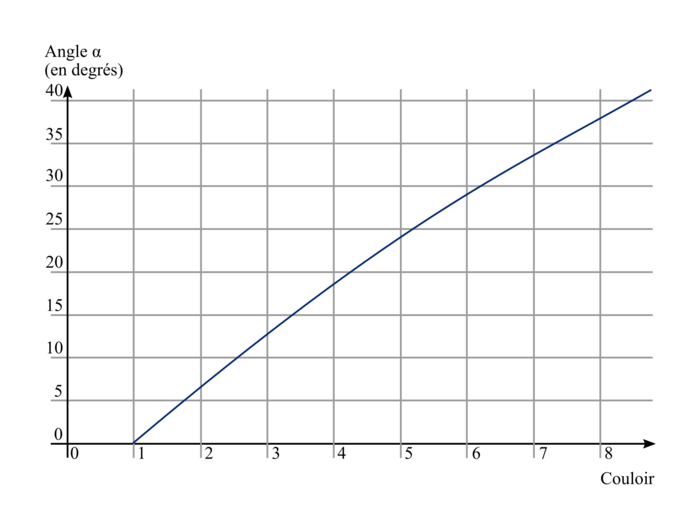 |
c) Y a-t-il proportionnalité entre le numéro du couloir et la valeur de α ? Justifier.
d) Par lecture graphique, donner un encadrement d'amplitude 2° de la valeur de l'angle α pour le couloir 3.
e) Un élève utilise un tableur pour déterminer automatiquement le décalage et l'angle en fonction du couloir.
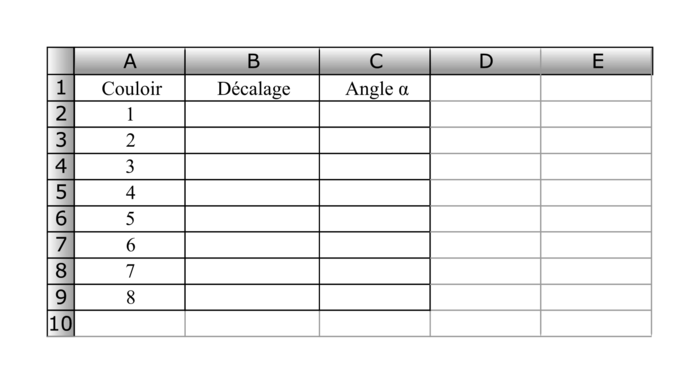 |
Parmi les formules suivantes, quelle formule, qu'il fera ensuite glisser dans toute la colonne, peut-il entrer dans la case B2 pour calculer le décalage ? On rappelle que « PI() » renvoie le nombre π.
Formule A : =PI()*((A2)*1,22+31,83)-100
Formule B : =PI()*((A2-1)*1,22+31,83)-100
Formule C : =PI()*((A2)*1,22)-100
Formule D : =PI()*((A2-1)*1,22)-100
Formule E : =PI()*((A2)*1,22+31,83)
Formule F : =PI()*((A2-1)*1,22+31,83)
Formule G : =PI()*((A2)*1,22)
Formule H : =PI()*((A2-1)*1,22)
Formule A : =PI()*((A2)*1,22+31,83)-100
Formule B : =PI()*((A2-1)*1,22+31,83)-100
Formule C : =PI()*((A2)*1,22)-100
Formule D : =PI()*((A2-1)*1,22)-100
Formule E : =PI()*((A2)*1,22+31,83)
Formule F : =PI()*((A2-1)*1,22+31,83)
Formule G : =PI()*((A2)*1,22)
Formule H : =PI()*((A2-1)*1,22)
5.
Au 1er janvier 2018, le jamaïcain Usain Boit détient le record du monde du 200 mètres en 19,19 secondes.
a) Déterminer sa vitesse moyenne en km/h. Arrondir au dixième.
b) À cette vitesse-là, combien mettrait-il de temps pour effectuer un marathon dont la longueur est de 42,195 km ? On donnera la réponse en heures, minutes et secondes, arrondie à la seconde près.
c) Le précédent record du monde du 200 mètres était détenu par l'américain Michael Johnson, « la locomotive de Wako », avec un temps de 19,32 secondes aux Jeux olympiques d'Atlanta en 1996. De quel pourcentage Usain Boit a-t-il réduit le temps du record du monde du 200 mètres ?
Deuxième partie (13 points)
Cette partie est composée de quatre exercices indépendants.
Exercice 1
Sur la figure ci-dessous, qui n'est pas dessinée en vraie grandeur, 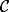 est un cercle de centre O et de rayon 5 cm. Le segment [AB] est un diamètre de ce cercle. Les points M et N sont les intersections du cercle
est un cercle de centre O et de rayon 5 cm. Le segment [AB] est un diamètre de ce cercle. Les points M et N sont les intersections du cercle 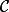 avec la médiatrice du segment [OB], Le point I est le milieu de [OB]. Le point S est le symétrique du point M par rapport au point O.
avec la médiatrice du segment [OB], Le point I est le milieu de [OB]. Le point S est le symétrique du point M par rapport au point O.
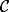 est un cercle de centre O et de rayon 5 cm. Le segment [AB] est un diamètre de ce cercle. Les points M et N sont les intersections du cercle
est un cercle de centre O et de rayon 5 cm. Le segment [AB] est un diamètre de ce cercle. Les points M et N sont les intersections du cercle 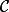 avec la médiatrice du segment [OB], Le point I est le milieu de [OB]. Le point S est le symétrique du point M par rapport au point O.
avec la médiatrice du segment [OB], Le point I est le milieu de [OB]. Le point S est le symétrique du point M par rapport au point O.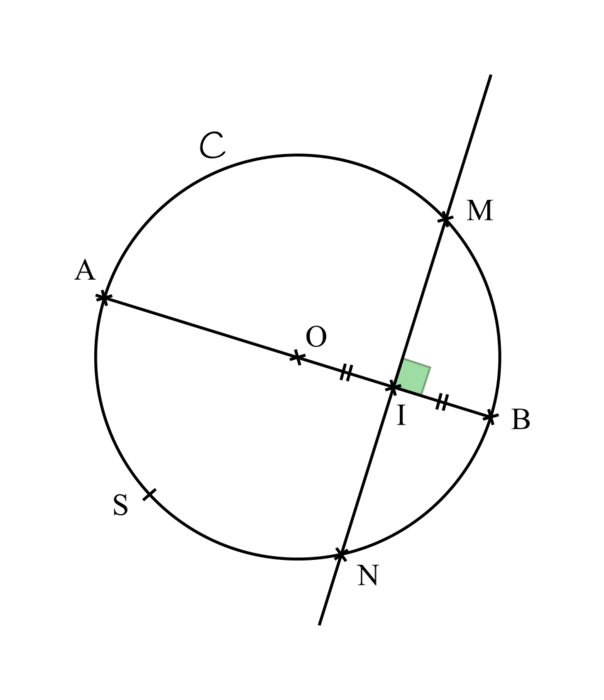 Cette figure n'est pas dessinée en vraie grandeur. |
1. Quelle est la nature du triangle OMB ? Justifier.
2. Démontrer que le quadrilatère AMBS est un rectangle.
3. Calculer la valeur exacte de l'aire du rectangle AMBS.
4. Démontrer que le quadrilatère OMBN est un losange.
Exercice 2
Indiquer si chacune des affirmations suivantes est vraie ou fausse. Justifier la réponse.
Une réponse inexacte ou non justifiée ne rapporte aucun point.
Une réponse inexacte ou non justifiée ne rapporte aucun point.
1. Affirmation 1 : 126 possède exactement 10 diviseurs.
2. Affirmation 2 : Si un polygone non croisé A a un périmètre supérieur au périmètre du polygone non croisé B, alors l'aire du polygone A est supérieure à l'aire du polygone B.
3. Affirmation 3 : Si des prix augmentent de 5 % par an, ils auront plus que doublé en 15 ans.
4. Affirmation 4 : Les dimensions de mon échantillon de parfum sont cinq fois plus petites que celles de mon flacon habituel. Il y a donc 25 fois moins de parfum dans l'échantillon que dans le flacon habituel.
Exercice 3
Un élève qui utilise le site « code.org » doit écrire un programme pour repasser au crayon noir les petits carrés en gris sur le dessin ci-dessous.
 |
Il propose le programme suivant :
 |
Quand il lance le programme, le dessin obtenu est le dessin ci-dessous.
 |
Que faut-il modifier dans le programme pour obtenir le dessin attendu ?
Exercice 4
Soit ABCDEFGH un cube d'arête 6 cm.
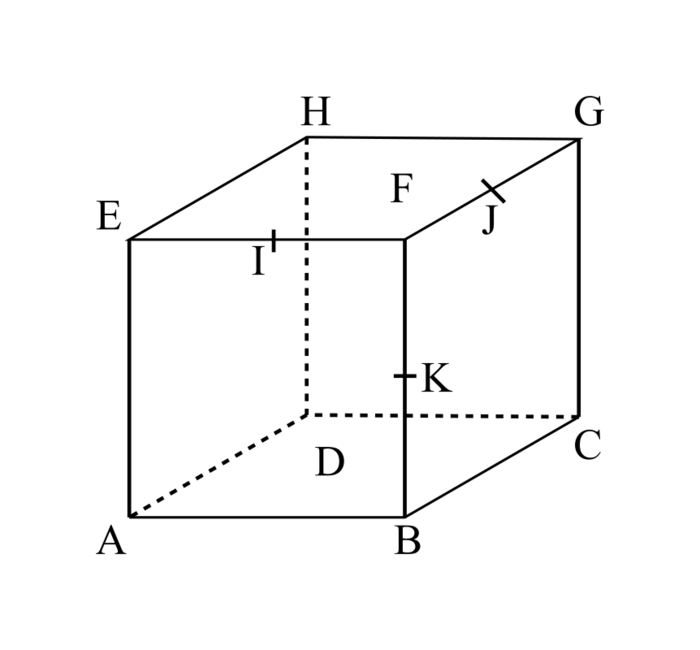 |
1. Soit I, J et K les milieux respectifs des arêtes [FE], [FG] et [FB].
Quelle est la nature du triangle IJK ? Justifier.
Quelle est la nature du triangle IJK ? Justifier.
2. Montrer que le volume du tétraèdre FIJK est 4,5 cm3. On rappelle que le volume d'une pyramide est égal au tiers du produit de l'aire d'une base par la hauteur associée.
3. Construire, en vraie grandeur, un patron du tétraèdre FIJK. On laissera les traits de construction.
4.
On coupe le cube en suivant le plan (IJK), afin d'ôter le tétraèdre FIJK.
On procède de la même façon avec chacun des sept autres sommets du cube.
Le solide obtenu après ces différentes coupes s'appelle un « cuboctaèdre ».
On procède de la même façon avec chacun des sept autres sommets du cube.
Le solide obtenu après ces différentes coupes s'appelle un « cuboctaèdre ».
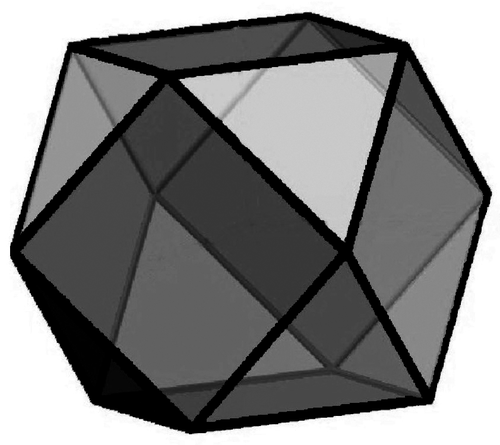 |
a) Calculer le volume de ce cuboctaèdre.
b) Calculer la longueur totale de ses arêtes. On donnera le résultat arrondi au millimètre.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Une enseignante de CM2 propose l'exercice suivant en classe de CM2.
| Une boîte contient des dragées toutes identiques. 120 dragées pèsent 360 g. Combien pèsent 30 dragées ? |
1. Proposer trois procédures pouvant être utilisées par les élèves pour résoudre cet exercice, en explicitant à chaque fois chacun des calculs effectués pour trouver le résultat attendu.
2. L'enseignante veut vérifier la maîtrise de la procédure dite de retour à l'unité par les élèves. Elle souhaite garder la même forme d'exercice en modifiant les nombres en jeu dans l'énoncé pour contraindre, ou au moins encourager vivement, les élèves à utiliser cette procédure. Proposer un énoncé modifié qu'elle pourrait soumettre à ses élèves.
Situation 2
Un professeur des écoles distribue le problème suivant à ses élèves de CE1 et leur demande de se mettre en groupes pour le résoudre. Les productions de quatre groupes sont présentées dans la suite.
| Les cinq élèves de l'équipe verte ont gagné des images. Lisa : 12 images ; Luc : 10 images ; Ilyes : 9 images ; Camille : 11 images ; Nora : 13 images. Ils veulent se les partager pour que chacun en ait la même quantité. Combien d'images aura chaque enfant après le partage ? |
1. Citer deux objectifs d'apprentissage que cette situation permet de travailler.
2.
a) Expliquer chacune des stratégies d'addition pour trouver 55 pour les élèves des groupes 1 et 2 en s'appuyant sur leurs productions ci-après.
b) Donner un point commun et deux différences dans la démarche mathématique des productions des groupes 1 et 2.
 |
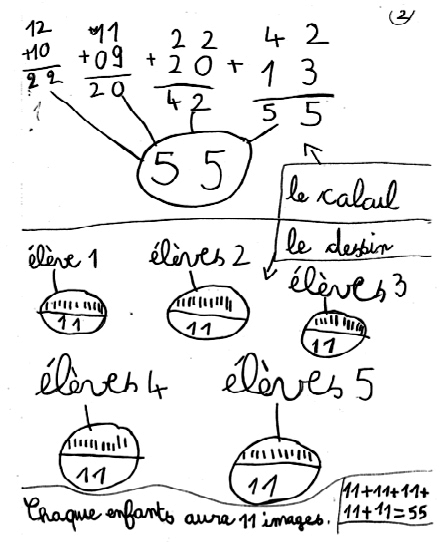 |
3. Citer deux difficultés qu'a rencontrées le groupe 3.
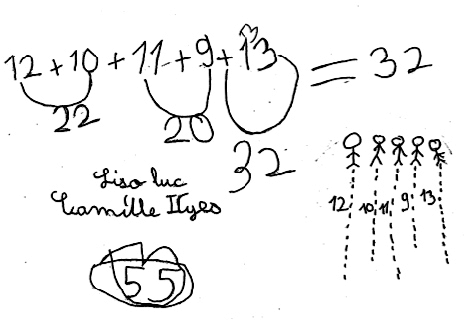 |
Situation 3
Voici une situation problème proposée à des élèves de CM1.
| Problème 1 Combien de sacs de 12 billes peut-on faire avec 56 billes ? |
Voici trois productions d'élèves illustrant la résolution du problème 1.
 |
 |
 |
1. Pour chacune de ces productions, expliciter la procédure utilisée pour résoudre le problème 1.
2. Expliquer comment la modification des nombres de l'énoncé peut montrer les limites des procédures mises en œuvre et inciter à l'utilisation de la technique opératoire de la division.
3. Citer trois connaissances ou capacités nécessaires pour effectuer une division posée.
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
1. Distance d'un tour de piste parcourue par le coureur 1
Le tour de piste d'un coureur au couloir 1 est constitué de deux lignes droites de longueur 100 m chacune et de deux demi-cercles, soit un cercle, de rayon 31,83 m.
Ce cercle a pour longueur : 2 × π × 31,83 m = π × 63,66 m.
La longueur du tour de piste est donc : 2 × 100 m + π × 63,66 m 399,99 m.
399,99 m.
Le tour de piste en couloir 1 a une longueur d'environ 400 m.
Le tour de piste d'un coureur au couloir 1 est constitué de deux lignes droites de longueur 100 m chacune et de deux demi-cercles, soit un cercle, de rayon 31,83 m.
Ce cercle a pour longueur : 2 × π × 31,83 m = π × 63,66 m.
La longueur du tour de piste est donc : 2 × 100 m + π × 63,66 m
 399,99 m.
399,99 m.Le tour de piste en couloir 1 a une longueur d'environ 400 m.
2. Tracé du couloir 1 à l'échelle 1/1 200
Les mesures utiles sont la longueur de la ligne droite et le rayon des demi-cercles intérieurs et extérieurs formant le couloir 1.
La ligne droite mesure 100 m. À l'échelle 1/1 200, 100 m correspondent à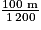 , soit environ 8,3 cm.
, soit environ 8,3 cm.
Le rayon des demi-cercles intérieurs mesure 31,83 m. À l'échelle 1/1 200, 31,83 m correspondent à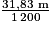 , soit environ 2,65 cm.
, soit environ 2,65 cm.
Le rayon des demi-cercles extérieurs mesure 33,05 m (car 31,83 + 1,22 = 33,05). À l'échelle 1/1 200, 33,05 m correspondent à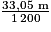 , soit environ 2,75 cm.
, soit environ 2,75 cm.
Les mesures utiles sont la longueur de la ligne droite et le rayon des demi-cercles intérieurs et extérieurs formant le couloir 1.
La ligne droite mesure 100 m. À l'échelle 1/1 200, 100 m correspondent à
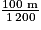 , soit environ 8,3 cm.
, soit environ 8,3 cm.Le rayon des demi-cercles intérieurs mesure 31,83 m. À l'échelle 1/1 200, 31,83 m correspondent à
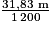 , soit environ 2,65 cm.
, soit environ 2,65 cm.Le rayon des demi-cercles extérieurs mesure 33,05 m (car 31,83 + 1,22 = 33,05). À l'échelle 1/1 200, 33,05 m correspondent à
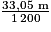 , soit environ 2,75 cm.
, soit environ 2,75 cm.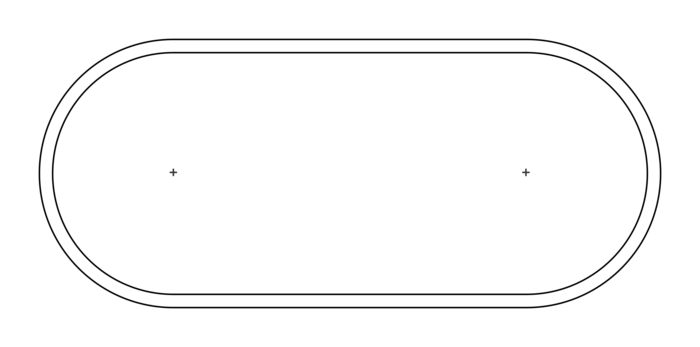 Cette figure est à l'échelle, mais pas à la taille demandée. |
3. Explication du non-alignement des coureurs au départ
Les rayons des demi-cercles ne sont pas les mêmes selon les couloirs, donc la longueur des demi-cercles parcourue, proportionnelle aux rayons, n'est pas la même non plus. La ligne d'arrivée étant perpendiculaire à la ligne droite, si l'on veut que tous les coureurs parcourent la même distance, il faut donc compenser les différences de longueur des demi-cercles par un échelonnement des départs : plus un coureur est à l'extérieur, plus il démarre en avant des autres.
Les rayons des demi-cercles ne sont pas les mêmes selon les couloirs, donc la longueur des demi-cercles parcourue, proportionnelle aux rayons, n'est pas la même non plus. La ligne d'arrivée étant perpendiculaire à la ligne droite, si l'on veut que tous les coureurs parcourent la même distance, il faut donc compenser les différences de longueur des demi-cercles par un échelonnement des départs : plus un coureur est à l'extérieur, plus il démarre en avant des autres.
4.
a) Calcul du décalage du coureur au couloir 6
Le décalage du coureur au couloir 6 correspond à la différence de longueur des demi-cercles des couloirs 1 et 6.
Au couloir 1, le demi-cercle a une longueur mesurant : π × 31,83 m.
Le rayon du demi-cercle au couloir 6 est : 31,83 m + 5 × 1,22 m = 31,83 m + 6,1 m.
La longueur du demi-cercle correspondant mesure donc : π × (31,83 + 6,1) m.
La différence de longueur est donc : π × 6,1 m 19,16 m.
19,16 m.
Le décalage du coureur au couloir 6 est d'environ 19,16 m.
Le décalage du coureur au couloir 6 correspond à la différence de longueur des demi-cercles des couloirs 1 et 6.
Au couloir 1, le demi-cercle a une longueur mesurant : π × 31,83 m.
Le rayon du demi-cercle au couloir 6 est : 31,83 m + 5 × 1,22 m = 31,83 m + 6,1 m.
La longueur du demi-cercle correspondant mesure donc : π × (31,83 + 6,1) m.
La différence de longueur est donc : π × 6,1 m
 19,16 m.
19,16 m.Le décalage du coureur au couloir 6 est d'environ 19,16 m.
b) Calcul de la mesure de l'angle α pour le couloir 6
L'angle au centre et la longueur d'arc correspondante sont proportionnels.
Pour un angle au centre de 180°, la longueur d'arc (qui est aussi la longueur du demi-cercle) est : π × (31,83 + 6,1) m = π × 37,93 m.
Pour 1 m de longueur d'arc, l'angle au centre correspondant est :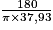 degrés.
degrés.
Pour une longueur d'arc de π × 6,1 m, l'angle au centre est en degrés :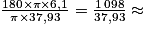 28,9.
28,9.
Au couloir 6, l'angle α mesure environ 28,9°.
L'angle au centre et la longueur d'arc correspondante sont proportionnels.
Pour un angle au centre de 180°, la longueur d'arc (qui est aussi la longueur du demi-cercle) est : π × (31,83 + 6,1) m = π × 37,93 m.
Pour 1 m de longueur d'arc, l'angle au centre correspondant est :
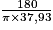 degrés.
degrés.Pour une longueur d'arc de π × 6,1 m, l'angle au centre est en degrés :
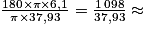 28,9.
28,9.Au couloir 6, l'angle α mesure environ 28,9°.
c) Relation entre le numéro du couloir et la valeur de l'angle α
Il n'y a pas proportionnalité entre le numéro du couloir et la valeur de l'angle α car la représentation graphique n'est pas une droite passant par l'origine : la courbe n'est pas une droite, et elle ne passe pas par 0.
Il n'y a pas proportionnalité entre le numéro du couloir et la valeur de l'angle α car la représentation graphique n'est pas une droite passant par l'origine : la courbe n'est pas une droite, et elle ne passe pas par 0.
Remarque
On privilégie un argument strictement graphique, ce qui est induit par le sujet. Sinon, on pouvait aussi dire que : au couloir 1, l'angle α vaut 0°, alors qu'au couloir 6 l'angle α vaut environ 28,9°. La linéarité multiplicative n'est donc pas vérifiée.d) Lecture graphique de la valeur de α pour le couloir 3
Au couloir 3, l'angle α est compris entre 12° et 14°.
Au couloir 3, l'angle α est compris entre 12° et 14°.
e) Formule à entrer en B2 pour le calcul de la valeur du décalage
Il s'agit, au choix, de la formule B ou de la formule H, qui fournissent les mêmes résultats, à 3 mm près, ce que l'on peut négliger.
Il s'agit, au choix, de la formule B ou de la formule H, qui fournissent les mêmes résultats, à 3 mm près, ce que l'on peut négliger.
5.
a) Calcul de la vitesse moyenne d'Usain Bolt
Usain Bolt a parcouru 200 m en 19,19 s. Cela correspond à une distance parcourue en une seconde de :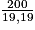 m. La distance parcourue en une heure, soit 3 600 s, est donc : 3 600 ×
m. La distance parcourue en une heure, soit 3 600 s, est donc : 3 600 × 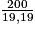 m
m  37,5 km.
37,5 km.
La vitesse moyenne d'Usain Bolt est d'environ 37,5 km/h.
Usain Bolt a parcouru 200 m en 19,19 s. Cela correspond à une distance parcourue en une seconde de :
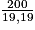 m. La distance parcourue en une heure, soit 3 600 s, est donc : 3 600 ×
m. La distance parcourue en une heure, soit 3 600 s, est donc : 3 600 × 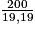 m
m  37,5 km.
37,5 km.La vitesse moyenne d'Usain Bolt est d'environ 37,5 km/h.
b) Durée d'un marathon couru à cette vitesse
Si l'on parcourt 37,5 km en 3 600 s, alors on parcourt 42,195 km en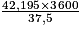 s, soit environ 4 051 s.
s, soit environ 4 051 s.
On a : 4 051 = 1 × 3 600 + 451 et 451 = 7 × 60 + 31.
D'où : 4 051 s = 1 h 7 min 31 s.
La durée de parcours d'un marathon à la vitesse d'Usain Bolt serait : 1 h 7 min 31 s.
Si l'on parcourt 37,5 km en 3 600 s, alors on parcourt 42,195 km en
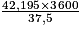 s, soit environ 4 051 s.
s, soit environ 4 051 s.On a : 4 051 = 1 × 3 600 + 451 et 451 = 7 × 60 + 31.
D'où : 4 051 s = 1 h 7 min 31 s.
La durée de parcours d'un marathon à la vitesse d'Usain Bolt serait : 1 h 7 min 31 s.
c) Pourcentage de réduction de vitesse d'Usain Bolt par rapport à Michael Johnson
On a : 19,32 − 19,19 = 0,13.
Usain Bolt a donc réduit la durée de course de 0,13 s. Le record précédent était de 19,32 s, et :
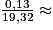 0,007.
0,007.
La réduction de vitesse représente donc un pourcentage de 0,7 % par rapport au record précédent.
On a : 19,32 − 19,19 = 0,13.
Usain Bolt a donc réduit la durée de course de 0,13 s. Le record précédent était de 19,32 s, et :
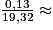 0,007.
0,007.La réduction de vitesse représente donc un pourcentage de 0,7 % par rapport au record précédent.
Deuxième partie
Exercice 1
1. Nature du triangle OMB
M est sur la médiatrice du segment [OB], donc OM = MB car la médiatrice d'un segment est le lieu des points équidistants des deux extrémités du segment.
Par ailleurs, M et B sont sur le cercle de centre O, donc : OM = OB.
Finalement : OM = OB = BM.
Le triangle OMB est équilatéral.
M est sur la médiatrice du segment [OB], donc OM = MB car la médiatrice d'un segment est le lieu des points équidistants des deux extrémités du segment.
Par ailleurs, M et B sont sur le cercle de centre O, donc : OM = OB.
Finalement : OM = OB = BM.
Le triangle OMB est équilatéral.
2. Preuve que AMBS est un rectangle
Le point S est le symétrique de M par rapport à O ; or M est sur le cercle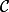 , de centre O. Ce cercle admet O comme centre de symétrie, on en déduit que S est sur
, de centre O. Ce cercle admet O comme centre de symétrie, on en déduit que S est sur 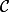 .
.
Les points M et S sont tous deux sur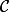 et alignés avec le centre O du cercle, [SM] est donc un diamètre de
et alignés avec le centre O du cercle, [SM] est donc un diamètre de 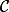 , tout comme [AB], par hypothèse.
, tout comme [AB], par hypothèse.
Les segments [MS] et [AB] ont donc même longueur et même milieu.
Ces segments sont les diagonales du quadrilatère AMBS. Or : « Si un quadrilatère a des diagonales de même longueur qui se coupent en leur milieu, alors c'est un rectangle. »
On en déduit que AMBS est un rectangle.
Le point S est le symétrique de M par rapport à O ; or M est sur le cercle
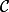 , de centre O. Ce cercle admet O comme centre de symétrie, on en déduit que S est sur
, de centre O. Ce cercle admet O comme centre de symétrie, on en déduit que S est sur 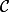 .
.Les points M et S sont tous deux sur
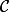 et alignés avec le centre O du cercle, [SM] est donc un diamètre de
et alignés avec le centre O du cercle, [SM] est donc un diamètre de 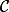 , tout comme [AB], par hypothèse.
, tout comme [AB], par hypothèse.Les segments [MS] et [AB] ont donc même longueur et même milieu.
Ces segments sont les diagonales du quadrilatère AMBS. Or : « Si un quadrilatère a des diagonales de même longueur qui se coupent en leur milieu, alors c'est un rectangle. »
On en déduit que AMBS est un rectangle.
3. Aire du rectangle AMBS
Le rectangle AMBS a pour longueur AM et pour largeur MB.
Son aire est donc : AM × MB.
On sait, d'après la question 1., que MB = OB et, par hypothèse, que OB = 5 cm, donc MB = 5 cm.
Reste à calculer AM.
Le triangle AMB est rectangle en M. D'après le théorème de Pythagore, AM2 + MB2 = AB2.
On a donc : AM =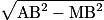 .
.
Or, AB = 10 cm, car c'est un diamètre du cercle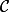 , et : BM = 5 cm.
, et : BM = 5 cm.
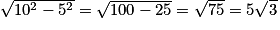 , donc : AM =
, donc : AM = 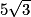 cm
cm
L'aire du rectangle AMBS est donc : (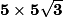 ) cm2 =
) cm2 = 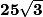 cm2.
cm2.
Le rectangle AMBS a pour longueur AM et pour largeur MB.
Son aire est donc : AM × MB.
On sait, d'après la question 1., que MB = OB et, par hypothèse, que OB = 5 cm, donc MB = 5 cm.
Reste à calculer AM.
Le triangle AMB est rectangle en M. D'après le théorème de Pythagore, AM2 + MB2 = AB2.
On a donc : AM =
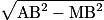 .
.Or, AB = 10 cm, car c'est un diamètre du cercle
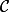 , et : BM = 5 cm.
, et : BM = 5 cm.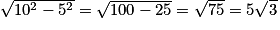 , donc : AM =
, donc : AM = 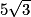 cm
cmL'aire du rectangle AMBS est donc : (
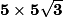 ) cm2 =
) cm2 = 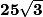 cm2.
cm2.4. OMBN est un losange (démonstration)
M et N sont tous deux sur la médiatrice de [OB], donc : MB = MO et NB = NO.
Par ailleurs, M et N sont sur le cercle de centre O, donc : OM = ON.
Finalement, MB = OM = ON = NB.
Les quatre côtés du quadrilatère OMBN sont de même longueur, donc OMBN est un losange.
M et N sont tous deux sur la médiatrice de [OB], donc : MB = MO et NB = NO.
Par ailleurs, M et N sont sur le cercle de centre O, donc : OM = ON.
Finalement, MB = OM = ON = NB.
Les quatre côtés du quadrilatère OMBN sont de même longueur, donc OMBN est un losange.
Exercice 2
Remarque
Pour justifier qu'une affirmation est fausse, on peut, selon les cas, résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, ou encore démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou bien démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
1. On a : 126 = 2 × 32 × 7 = 21 × 32 × 71
Le nombre 126 a donc : (1 + 1)(2 + 1)(1 + 1) = 12 diviseurs.
Conclusion : l'affirmation est fausse.
Le nombre 126 a donc : (1 + 1)(2 + 1)(1 + 1) = 12 diviseurs.
Conclusion : l'affirmation est fausse.
Remarque
On utilise ici le résultat suivant : si la décomposition d'un nombre en produit de nombres premiers est axbycz…, alors son nombre de diviseurs est : (x + 1)(y + 1)(z + 1)…2. Considérons le rectangle A, de longueur 6 cm et de largeur 2,5 cm. Son périmètre est donc 17 cm et son aire 15 cm2 car : 2 × (2,5 + 6) = 17 et 2,5 × 6 = 15.
Considérons à présent un carré B de côté 4 cm. Son périmètre est 16 cm et son aire 16 cm2 car : 4 × 4 = 16.
Le périmètre de A est donc supérieur à celui de B, alors que l'aire de A est inférieure à celle de B.
Conclusion : l'affirmation est fausse.
Considérons à présent un carré B de côté 4 cm. Son périmètre est 16 cm et son aire 16 cm2 car : 4 × 4 = 16.
Le périmètre de A est donc supérieur à celui de B, alors que l'aire de A est inférieure à celle de B.
Conclusion : l'affirmation est fausse.
3. En quinze ans, le prix est multiplié par 1,0515. Or 1,0515  2,08. Le prix aura donc plus que doublé en 15 ans.
2,08. Le prix aura donc plus que doublé en 15 ans.
Conclusion : l'affirmation est vraie.
 2,08. Le prix aura donc plus que doublé en 15 ans.
2,08. Le prix aura donc plus que doublé en 15 ans.Conclusion : l'affirmation est vraie.
4. Si les dimensions de l'échantillon sont cinq fois plus petites que celles du flacon habituel, cela signifie que l'échantillon est une réduction de l'original de rapport 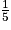 . Or, on sait que, lors d'une réduction de rapport k, les volumes sont réduits dans le rapport k3.
. Or, on sait que, lors d'une réduction de rapport k, les volumes sont réduits dans le rapport k3.
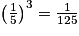 .
.
Il y a donc 125 fois (et non 25 fois) moins de parfum dans l'échantillon que dans le flacon habituel.
Conclusion : l'affirmation est fausse.
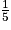 . Or, on sait que, lors d'une réduction de rapport k, les volumes sont réduits dans le rapport k3.
. Or, on sait que, lors d'une réduction de rapport k, les volumes sont réduits dans le rapport k3.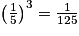 .
.Il y a donc 125 fois (et non 25 fois) moins de parfum dans l'échantillon que dans le flacon habituel.
Conclusion : l'affirmation est fausse.
Exercice 3
Il faut remplacer : « répéter 7 fois » par : « répéter 8 fois » et « saute en avant de 20 pixels » par : « saute en avant de 40 pixels » pour obtenir le résultat attendu.Exercice 4
1. Nature du triangle IJK
Dans le triangle EFG : I est le milieu de [EF] et J le milieu de [FG]. D'après la propriété de la droite des milieux, on en déduit que : IJ =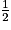 EG.
EG.
De même : IK =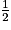 EB et JK =
EB et JK = 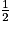 GB.
GB.
Les faces du cube étant toutes superposables, on a : EG = EB = GB, d'où : IJ = IK = JK.
Le triangle IJK est donc équilatéral.
Dans le triangle EFG : I est le milieu de [EF] et J le milieu de [FG]. D'après la propriété de la droite des milieux, on en déduit que : IJ =
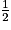 EG.
EG.De même : IK =
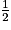 EB et JK =
EB et JK = 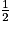 GB.
GB.Les faces du cube étant toutes superposables, on a : EG = EB = GB, d'où : IJ = IK = JK.
Le triangle IJK est donc équilatéral.
2. Volume du tétraèdre FIJK
Remarque
La question précédente « pousse » à regarder le tétraèdre FIJK comme étant de base IJK et de sommet F. Le calcul de l'aire du triangle IJK, et encore plus celui de la hauteur issue de F sont toutefois ardus. Il faut donc changer de perspective, ce qui est possible dans le cas particulier du tétraèdre, chacune des faces pouvant être considérée comme base.Considérons le triangle IFK comme base du tétraèdre FIJK ; le sommet correspondant est alors J, et la hauteur JF.
I, J et K étant les milieux respectifs de [EF], [FG] et [FB], on a : IF = FJ = FK = 6 cm ÷ 2 = 3 cm.
D'où : VolumeFIJK =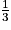 AireIFK × FJ =
AireIFK × FJ = 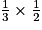 × IF × FK × FJ.
× IF × FK × FJ.
On a donc : VolumeFIJK =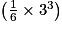 cm3 = 4,5 cm3.
cm3 = 4,5 cm3.
Le volume du tétraèdre FIJK est bien 4,5 cm3.
I, J et K étant les milieux respectifs de [EF], [FG] et [FB], on a : IF = FJ = FK = 6 cm ÷ 2 = 3 cm.
D'où : VolumeFIJK =
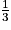 AireIFK × FJ =
AireIFK × FJ = 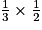 × IF × FK × FJ.
× IF × FK × FJ.On a donc : VolumeFIJK =
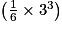 cm3 = 4,5 cm3.
cm3 = 4,5 cm3.Le volume du tétraèdre FIJK est bien 4,5 cm3.
3. Construction du patron du tétraèdre FIJK
Remarque
En l'absence d'information contraire, on considère que tous les instruments de géométrie sont autorisés.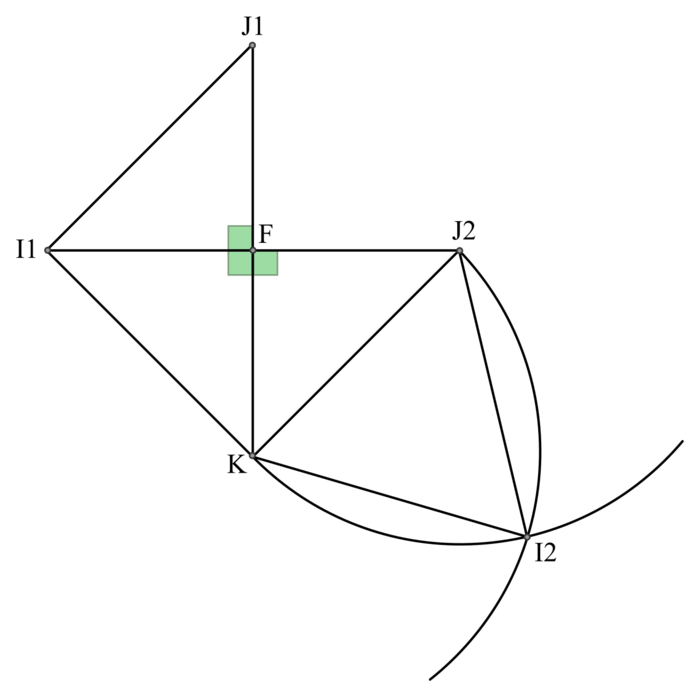 Cette figure est à l'échelle, mais pas à la taille demandée. |
4.
a) Volume du cuboctaèdre
Le cuboctaèdre est obtenu à partir du cube ABCDEFGH, en retirant huit tétraèdres identiques au tétraèdre FIJK.
On a donc : Volumecuboctaèdre = Volumecube − 8 × Volumetétraèdre.
Or : Volumecube = 63 cm3 = 216 cm3 et Volumetétraèdre = 4,5 cm3 (d'après la question 2.).
D'où : Volumecuboctaèdre = (216 − 8 × 4,5) cm3 = 180 cm3.
Le cuboctaèdre a un volume de 180 cm3.
Le cuboctaèdre est obtenu à partir du cube ABCDEFGH, en retirant huit tétraèdres identiques au tétraèdre FIJK.
On a donc : Volumecuboctaèdre = Volumecube − 8 × Volumetétraèdre.
Or : Volumecube = 63 cm3 = 216 cm3 et Volumetétraèdre = 4,5 cm3 (d'après la question 2.).
D'où : Volumecuboctaèdre = (216 − 8 × 4,5) cm3 = 180 cm3.
Le cuboctaèdre a un volume de 180 cm3.
b) Longueur totale des arêtes du cuboctaèdre
Remarque
Ces arêtes correspondent aux côtés des triangles équilatéraux de base des huit tétraèdres « coupés ».Le cuboctaèdre a 24 arêtes, toutes de même longueur que IJ.
On a : IJ =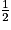 EG (d'après la question 1.).
EG (d'après la question 1.).
EG est la diagonale d'un carré de côté 6 cm, donc EG =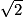 × 6 cm.
× 6 cm.
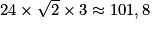 .
.
La longueur totale des arêtes du cuboctaèdre est donc environ 101,8 cm.
On a : IJ =
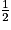 EG (d'après la question 1.).
EG (d'après la question 1.).EG est la diagonale d'un carré de côté 6 cm, donc EG =
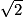 × 6 cm.
× 6 cm.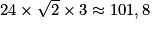 .
.La longueur totale des arêtes du cuboctaèdre est donc environ 101,8 cm.
Troisième partie
Situation 1
1. Trois procédures de résolution en CM2
L'exercice proposé est un problème de proportionnalité.
L'exercice proposé est un problème de proportionnalité.
• 1re procédure : utilisation de la linéarité multiplicative
L'élève observe que 30 = 120 ÷ 4. Il effectue ensuite la division 360 ÷ 4 et trouve 90.
Dans les deux cas, le calcul peut être effectué en ligne ou de tête, en s'appuyant sur la connaissance de la table de 4 et sur l'interprétation des nombres 120 et 360 comme 12 (resp. 36) dizaines, puis la conversion de 4 (resp. 9) dizaines comme 40 (resp. 90) unités.
L'élève observe que 30 = 120 ÷ 4. Il effectue ensuite la division 360 ÷ 4 et trouve 90.
Dans les deux cas, le calcul peut être effectué en ligne ou de tête, en s'appuyant sur la connaissance de la table de 4 et sur l'interprétation des nombres 120 et 360 comme 12 (resp. 36) dizaines, puis la conversion de 4 (resp. 9) dizaines comme 40 (resp. 90) unités.
• 2e procédure : utilisation du rapport constant
L'élève observe que 360 = 3 × 120. Il effectue : 30 × 3 = 3 × 10 × 3 = 3 × 3 × 10 = 9 × 10 = 90.
L'élève observe que 360 = 3 × 120. Il effectue : 30 × 3 = 3 × 10 × 3 = 3 × 3 × 10 = 9 × 10 = 90.
• 3e procédure : passage par l'unité
L'élève calcule la masse d'une dragée en effectuant 360 ÷ 120 ; après avoir trouvé 3, il effectue le produit 30 × 3 et trouve 90.
L'élève calcule la masse d'une dragée en effectuant 360 ÷ 120 ; après avoir trouvé 3, il effectue le produit 30 × 3 et trouve 90.
2. Énoncé privilégiant la procédure de retour à l'unité
Le passage par l'unité ne présente pas ici d'avantage particulier en termes d'économie de moyens ou de fiabilité. Pour encourager les élèves à utiliser cette procédure, il faut que cette méthode soit plus avantageuse que l'utilisation de la linéarité multiplicative ou additive et que les rapports constants.
Proposition : « Une boîte contient des dragées toutes identiques.
17 dragées pèsent 68 g. Combien pèsent 13 dragées ? »
Le rapport multiplicatif entre 17 et 68 est moins évident, et celui entre 17 et 13 irrationnel.
Les élèves sont donc clairement incités à calculer la masse d'une dragée.
Le passage par l'unité ne présente pas ici d'avantage particulier en termes d'économie de moyens ou de fiabilité. Pour encourager les élèves à utiliser cette procédure, il faut que cette méthode soit plus avantageuse que l'utilisation de la linéarité multiplicative ou additive et que les rapports constants.
Proposition : « Une boîte contient des dragées toutes identiques.
17 dragées pèsent 68 g. Combien pèsent 13 dragées ? »
Le rapport multiplicatif entre 17 et 68 est moins évident, et celui entre 17 et 13 irrationnel.
Les élèves sont donc clairement incités à calculer la masse d'une dragée.
Remarque
On a également veillé à la plausibilité des données, avec une masse unitaire de 4 g.Situation 2
1. Objectifs d'apprentissage visés par cette situation
Cette situation permet de travailler la capacité à résoudre un problème complexe (se représenter la situation, imaginer une procédure personnelle de résolution, la mettre en œuvre et interpréter ses résultats).
Un autre objectif est l'apprentissage du travail en groupe (collaborer, argumenter, entendre les arguments des autres, etc.).
Cette situation permet de travailler la capacité à résoudre un problème complexe (se représenter la situation, imaginer une procédure personnelle de résolution, la mettre en œuvre et interpréter ses résultats).
Un autre objectif est l'apprentissage du travail en groupe (collaborer, argumenter, entendre les arguments des autres, etc.).
2.
a) Stratégies d'addition des groupes 1 et 2
• Le groupe 1 commence par décomposer mentalement les nombres en dizaines et unités. Il additionne les dizaines, puis ajoute au résultat les unités restantes. Le calcul est effectué en ligne.
Remarque
L'écriture est mathématiquement fausse, mais usuelle (et tolérée) à cet âge.• Le groupe 2 pose des additions : il additionne deux à deux quatre des données de l'énoncé : 12 et 10, 11 et 9 (ces deux dernières peut-être parce que le calcul est aisé), puis pose l'addition des deux résultats obtenus, avant de poser une ultime addition du résultat avec la dernière donnée.
Remarque
Il est à noter que les deux groupes trouvent la réponse escomptée.b) Point commun et deux différences dans les démarches des groupes 1 et 2
• Point commun : les deux groupes additionnent le nombre d'images obtenues par chacun des personnages de l'énoncé.
Autre point commun : les deux groupes représentent le partage entre les cinq enfants par une distribution un à un de points ou de bâtons en regard de cinq emplacements matérialisant les cinq enfants.
Autre point commun : les deux groupes représentent le partage entre les cinq enfants par une distribution un à un de points ou de bâtons en regard de cinq emplacements matérialisant les cinq enfants.
• Différences :
- le groupe 1 effectue l'addition en ligne alors que le groupe 2 pose des additions (voir question 2.a)) ;
- le groupe 1 formule explicitement que le partage relève d'une division, ce que ne fait pas le groupe 2 ;
- le groupe 2 vérifie le résultat du partage en effectuant en ligne l'addition itérée 5 fois de 11, alors que le groupe 1 ne rend pas compte d'une quelconque vérification.
3. Deux difficultés rencontrées par le groupe 3
Le groupe 3 a tout d'abord des difficultés à effectuer l'addition des cinq données : le calcul en ligne est bien écrit, mais le résultat erroné. Les élèves ont correctement calculé mentalement les sommes partielles 12 + 10 et 11 + 9, mais ne parviennent pas à gérer la suite du calcul.
Le groupe 3 a tout d'abord des difficultés à effectuer l'addition des cinq données : le calcul en ligne est bien écrit, mais le résultat erroné. Les élèves ont correctement calculé mentalement les sommes partielles 12 + 10 et 11 + 9, mais ne parviennent pas à gérer la suite du calcul.
Remarque
Le résultat correct apparaît au bas la copie, mais sans explications ; il est possible que ce résultat ait été ajouté lors d'une mise en commun ou communication avec un autre groupe.Par ailleurs, les élèves ont des difficultés à se représenter et à mobiliser une procédure correspondant au partage du total des images.
Remarque
Le dessin réalisé correspond à la situation initiale ; peut-être le temps passé à la réalisation de ce dessin n'a-t-il pas permis aux élèves d'avoir le loisir de concevoir la fin de la résolution du problème.Situation 3
1. Procédures de résolution utilisées
Remarque
La question porte exclusivement sur la procédure de résolution et non sur une analyse plus générale de la production, erreurs comprises. Nous donnons toutefois, en italique, des compléments d'analyse.• Production 1
L'élève calcule en ligne l'addition itérée 5 fois de 12. Il trouve 60, qu'il compare à 56. Se rendant compte que le résultat obtenu est trop grand, il barre un terme 12, recalcule la somme ou retranche 12 à 60, trouve 48 et conclut.
Alors que cela n'était pas demandé, il indique aussi le nombre de billes restant, résultat obtenu en posant et effectuant la soustraction « 56 − 48 ».
L'élève calcule en ligne l'addition itérée 5 fois de 12. Il trouve 60, qu'il compare à 56. Se rendant compte que le résultat obtenu est trop grand, il barre un terme 12, recalcule la somme ou retranche 12 à 60, trouve 48 et conclut.
Alors que cela n'était pas demandé, il indique aussi le nombre de billes restant, résultat obtenu en posant et effectuant la soustraction « 56 − 48 ».
• Production 2
L'élève procède à des soustractions posées successives de 12, à partir de 56. Il numérote en regard les retraits. Il conclut en indiquant également le nombre de billes restant, qui correspond à la dernière différence, inférieure à 12.
L'élève procède à des soustractions posées successives de 12, à partir de 56. Il numérote en regard les retraits. Il conclut en indiquant également le nombre de billes restant, qui correspond à la dernière différence, inférieure à 12.
• Production 3
L'élève écrit les multiples successifs de 12, jusqu'à 12 × 5, premier multiple dépassant 56. Il conclut, en indiquant le reste, calculé mentalement.
Une erreur sur les deux derniers multiples engendre une erreur sur le reste, sans conséquence quant à la réponse au problème posé.
L'élève écrit les multiples successifs de 12, jusqu'à 12 × 5, premier multiple dépassant 56. Il conclut, en indiquant le reste, calculé mentalement.
Une erreur sur les deux derniers multiples engendre une erreur sur le reste, sans conséquence quant à la réponse au problème posé.
2. Modification des valeurs numériques incitant à utiliser la technique opératoire de la division
L'addition itérée, tout comme les soustractions successives ou la liste des multiples, est une procédure coûteuse (temps et fiabilité) dès lors qu'il y a beaucoup de termes ou de multiples à considérer. Il faut donc accroître la quantité de termes potentiels, en augmentant la quantité de billes à partager, si l'on veut favoriser le recours à la division posée.
L'addition itérée, tout comme les soustractions successives ou la liste des multiples, est une procédure coûteuse (temps et fiabilité) dès lors qu'il y a beaucoup de termes ou de multiples à considérer. Il faut donc accroître la quantité de termes potentiels, en augmentant la quantité de billes à partager, si l'on veut favoriser le recours à la division posée.
3. Trois compétences ou capacités nécessaires à la réalisation d'une division posée
Pour effectuer une division posée, il faut :
Pour effectuer une division posée, il faut :
- connaître les tables de multiplication (faits numériques) ;
- savoir poser et effectuer une soustraction (pour obtenir les restes intermédiaires) ;
- connaître le système de numération (connaître les unités de numération et leurs liens) ;
- savoir décomposer un nombre selon différentes unités de numération ;
- savoir comparer des nombres entiers (comparaison entre dividendes et diviseur).
Remarque
Les trois premières réponses semblent être attendues, mais toutes les réponses parmi celles données sont valides.