Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (5 points)
Dans cet exercice, des affirmations sont proposées. Pour chacune d'entre elles, dire si elle est vraie ou si elle est fausse. Justifier la réponse.
Une réponse exacte mais non justifiée ne rapporte aucun point.
Une réponse fausse n'enlève pas de point.
Une réponse exacte mais non justifiée ne rapporte aucun point.
Une réponse fausse n'enlève pas de point.
1. La figure ci-dessous représente trois carrés construits sur les trois côtés d'un triangle rectangle. Dans chacun des carrés est indiquée son aire.
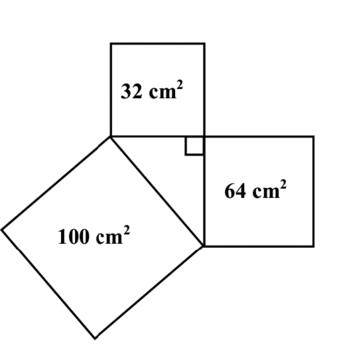 |
Affirmation 1 : « La construction à l'échelle de cette figure est possible. »
2. Affirmation 2 : « Si un nombre est multiple de 6 et de 9, alors il est aussi multiple de 54. »
3. On considère deux nombres dont la somme est 400.
Affirmation 3 : « Si l'on augmente de 3 chacun de ces deux nombres alors leur produit augmente de 1209. »
Affirmation 3 : « Si l'on augmente de 3 chacun de ces deux nombres alors leur produit augmente de 1209. »
4. En période de sécheresse, un agriculteur a des réserves pour alimenter ses 8 vaches pendant 20 jours. Il accepte de prendre en charge 2 vaches de plus pour rendre service à son voisin.
Affirmation 4 : « Avec ces mêmes réserves, il pourra nourrir toutes les vaches pendant 18 jours. »
Affirmation 4 : « Avec ces mêmes réserves, il pourra nourrir toutes les vaches pendant 18 jours. »
5.
On considère un solide constitué d'un empilement de cubes identiques.
On voit ci-contre les vues de droite, de face et de dessus.
On voit ci-contre les vues de droite, de face et de dessus.
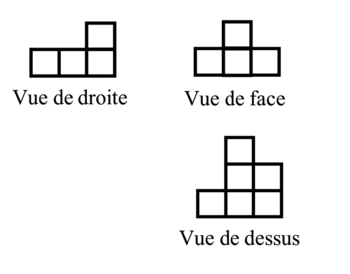 |
Affirmation 5 : « On peut construire un tel solide à l'aide d'un empilement de 7 cubes. »
6. Affirmation 6 : « En insérant de différentes manières exactement deux parenthèses (une ouvrante et une fermante) dans l'écriture 8 × 7 + 3 × 5, on peut obtenir tous les nombres de la liste suivante : 71 ; 176 ; 283 ; 295 ; 400. »
Exercice 2 (5 points)
Soit ABC un triangle isocèle, rectangle en A, tel que AB = 1 m.
On cherche à inscrire dans ce triangle un rectangle ayant une aire maximale.
Dans tout ce problème, l'unité de longueur est le mètre.
On cherche à inscrire dans ce triangle un rectangle ayant une aire maximale.
Dans tout ce problème, l'unité de longueur est le mètre.
Partie A :
Dans cette partie, on inscrit le rectangle AFED comme sur la figure ci-contre.
- F est un point du segment [AC] ;
- D est un point du segment [AB] ;
- E est un point du segment [BC].
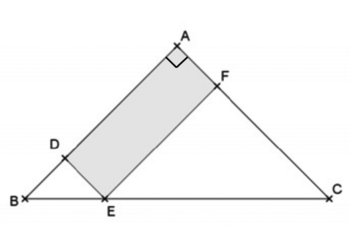 |
On pose AD = x et on considère la fonction f qui, à tout nombre x compris entre 0 et 1, associe l'aire du rectangle ADEF.
1. Montrer que : f(x) = −x2 + x.
2.
À l'aide d'une feuille de calcul, on a construit un tableau de valeurs de la fonction f.
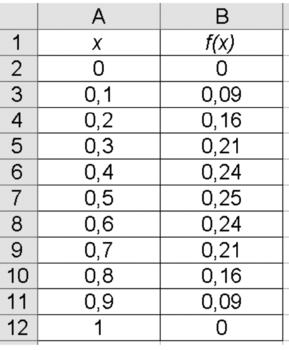 |
a) Quelle formule a-t-on pu entrer dans la cellule B2, puis recopier jusqu'en B12, pour générer les images par f ?
b) Dans cette question, on admet l'existence d'un maximum pour la fonction f. Peut-on affirmer, à l'aide du tableau, que le maximum de la fonction f est atteint en 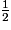 ?
?
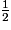 ?
?3. a) Démontrer que : f(x) = 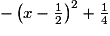
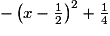
b) En déduire l'aire maximale recherchée.
c) Le rectangle d'aire maximale est-il un carré ?
Partie B :
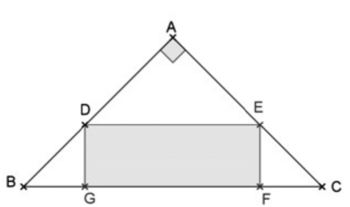
Dans cette partie, on inscrit le rectangle DEFG comme sur la figure ci-contre.
- D est un point du segment [AB] ;
- E est un point du segment [AC] ;
- G et F sont deux points du segment [BC].
 |
1. Dans quel intervalle I se trouve le nombre x ?
Dans la suite de l'exercice, on considère la fonction g qui, à tout nombre x dans l'intervalle I, associe l'aire du rectangle DEFG.
2. Exprimer g(x) en fonction de x.
3.
La représentation graphique de g est donnée ci-dessous :
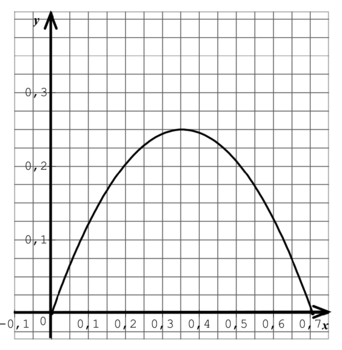 |
a) D'après le graphique, où placer le point G pour inscrire un rectangle d'aire 0,2 m2 ?
b) Par lecture graphique, déterminer l'aire maximale recherchée au centième près.
c) Pour cette aire, le quadrilatère DEFG est-il un carré ?
Exercice 3 (2 points)
Soit n un nombre entier naturel non nul et An le nombre entier naturel dont l'écriture décimale ne contient que le chiffre 1 répété n fois : An = 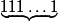
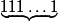
1. Pour quelles valeurs de n le nombre An est-il divisible par 11 ? Justifier.
2. Pour quelles valeurs de n le nombre An est-il divisible par 33 ? Justifier.
Corrigé
Corrigé
Exercice 1 (5 points)
Dans cet exercice, il est demandé au candidat d'indiquer, en justifiant, si des affirmations sont vraies ou fausses. Certaines de ces affirmations sont contextualisées ; il faut donc bien prendre le temps de lire attentivement les indications fournies.
Pour justifier qu'une affirmation est fausse, on peut, selon les cas : résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.
Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
Pour justifier qu'une affirmation est fausse, on peut, selon les cas : résoudre l'exercice et trouver un résultat autre que celui qui est annoncé, fournir un contre-exemple, démontrer que la proposition est fausse en prouvant un résultat incompatible avec celui proposé.
Pour prouver qu'une proposition est vraie, on peut résoudre l'exercice et trouver le résultat annoncé ou démontrer la vérité générale de la proposition, en utilisant des propriétés connues.
1. Affirmation 1 : La construction à l'échelle de cette figure est possible.
Cette question est extrêmement mal posée (et oui, cela arrive ! malheureusement…). En effet, il s'agissait de se positionner (sans que cela ne soit explicitement formulé) sur la présence ou non d'un angle droit dans le triangle représenté sur le dessin. Or, le fait même de mettre en question la présence de cet angle droit va à l'encontre des fondements de la géométrie, qui veulent que, si le dessin ne donne pas à voir – c'est-à-dire qu'une preuve ne peut être faite par la seule observation d'un dessin– il donne à savoir : le codage d'un angle droit doit donc être considéré comme une vérité (même si notre perception visuelle est autre). Par ailleurs, c'est la règle même de l'exercice qui est remise en question, puisque le triangle est prétendu rectangle dans la description du contexte, et que cette description ne doit pas être mise en question habituellement : le candidat doit, le contexte étant donné et indiscutable, se prononcer sur l'affirmation que l'on lui soumet. Il est à souhaiter que les candidats n'aient pas été trop « perturbés » par l'énoncé… Nous proposons une solution qui passe par la reformulation de l'affirmation.
Cette question est extrêmement mal posée (et oui, cela arrive ! malheureusement…). En effet, il s'agissait de se positionner (sans que cela ne soit explicitement formulé) sur la présence ou non d'un angle droit dans le triangle représenté sur le dessin. Or, le fait même de mettre en question la présence de cet angle droit va à l'encontre des fondements de la géométrie, qui veulent que, si le dessin ne donne pas à voir – c'est-à-dire qu'une preuve ne peut être faite par la seule observation d'un dessin– il donne à savoir : le codage d'un angle droit doit donc être considéré comme une vérité (même si notre perception visuelle est autre). Par ailleurs, c'est la règle même de l'exercice qui est remise en question, puisque le triangle est prétendu rectangle dans la description du contexte, et que cette description ne doit pas être mise en question habituellement : le candidat doit, le contexte étant donné et indiscutable, se prononcer sur l'affirmation que l'on lui soumet. Il est à souhaiter que les candidats n'aient pas été trop « perturbés » par l'énoncé… Nous proposons une solution qui passe par la reformulation de l'affirmation.
Se prononcer sur le fait que la figure soit constructible à l'échelle revient (sic) à se prononcer sur le fait que le triangle soit, ou non, rectangle.
Le carré de la longueur du plus grand côté est : 100.
La somme des carrés des longueurs des deux autres côtés est : 64 + 32 = 96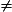 100.
100.
D'après la contraposée du théorème de Pythagore, on en déduit que le triangle n'est pas rectangle.
L'affirmation 1 est fausse.
Remarque : Lorsqu'une propriété dit que : « si P, alors Q », la contraposée dit que : « si non Q, alors non P ».
Le carré de la longueur du plus grand côté est : 100.
La somme des carrés des longueurs des deux autres côtés est : 64 + 32 = 96
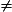 100.
100.D'après la contraposée du théorème de Pythagore, on en déduit que le triangle n'est pas rectangle.
L'affirmation 1 est fausse.
Remarque : Lorsqu'une propriété dit que : « si P, alors Q », la contraposée dit que : « si non Q, alors non P ».
2. Affirmation 2 : Si un nombre est multiple de 6 et de 9, alors il est aussi multiple de 54.
Remarque : On sait que tout multiple de p et q est multiple de pq lorsque p et q sont premiers entre eux, ce qui n'est pas le cas ici…
Remarque : On sait que tout multiple de p et q est multiple de pq lorsque p et q sont premiers entre eux, ce qui n'est pas le cas ici…
1ère méthode : réponse théorique générale
Tout multiple de 6 et 9 est aussi multiple du ppcm de 9 et 6. Comme 6 = 2 × 3 et 9 = 3 × 3, ppcm(6 ; 9) = 2 × 3 × 3 = 18 >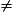 54. Il y a des multiples de 18 qui ne sont pas multiples de 54.
54. Il y a des multiples de 18 qui ne sont pas multiples de 54.
Tout multiple de 6 et 9 est aussi multiple du ppcm de 9 et 6. Comme 6 = 2 × 3 et 9 = 3 × 3, ppcm(6 ; 9) = 2 × 3 × 3 = 18 >
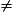 54. Il y a des multiples de 18 qui ne sont pas multiples de 54.
54. Il y a des multiples de 18 qui ne sont pas multiples de 54.2e méthode : contre-exemple
18 (ou 36) est un multiple de 6 et de 9, mais n'est pas un multiple de 54.
L'affirmation 2 est fausse.
18 (ou 36) est un multiple de 6 et de 9, mais n'est pas un multiple de 54.
L'affirmation 2 est fausse.
3. Affirmation 3 : Si on augmente de 3 chacun des deux nombres alors leur produit augmente de 1209.
Soient n et p les deux nombres considérés. On sait que : n + p = 400.
Alors : (n + 3)(p + 3) = np + 3p + 3n + 9 = np + 3(n + p) + 9 = np + 3 × 400 + 9 = np + 1209.
L'affirmation 3 est vraie.
Soient n et p les deux nombres considérés. On sait que : n + p = 400.
Alors : (n + 3)(p + 3) = np + 3p + 3n + 9 = np + 3(n + p) + 9 = np + 3 × 400 + 9 = np + 1209.
L'affirmation 3 est vraie.
4. Affirmation 4 : Avec les mêmes réserves, l'agriculteur pourra nourrir toutes les vaches pendant 18 jours.
Il s'agit d'un problème de double proportionnalité : la quantité de fourrage est proportionnelle au nombre de vaches (à durée constante) et à la durée (à nombre de vaches constant). Comme toujours dans le cas de la proportionnalité, les procédures sont multiples. Nous en proposons une ici.
Calcul du nombre de rations nécessaires dans les deux cas.
On prend comme référence la ration quotidienne d'une vache.
Si l'agriculteur peut nourrir 8 vaches pendant 20 jours, c'est qu'il dispose de 8 × 20 = 160 rations de fourrage.
Pour nourrir 10 vaches pendant 18 jours, il faut 10 × 18 = 180 rations de fourrage. Le fourrage en stock ne suffit donc pas.
On conclut : l'affirmation 4 est fausse.
Il s'agit d'un problème de double proportionnalité : la quantité de fourrage est proportionnelle au nombre de vaches (à durée constante) et à la durée (à nombre de vaches constant). Comme toujours dans le cas de la proportionnalité, les procédures sont multiples. Nous en proposons une ici.
Calcul du nombre de rations nécessaires dans les deux cas.
On prend comme référence la ration quotidienne d'une vache.
Si l'agriculteur peut nourrir 8 vaches pendant 20 jours, c'est qu'il dispose de 8 × 20 = 160 rations de fourrage.
Pour nourrir 10 vaches pendant 18 jours, il faut 10 × 18 = 180 rations de fourrage. Le fourrage en stock ne suffit donc pas.
On conclut : l'affirmation 4 est fausse.
5.
Affirmation 5 : On peut construire le solide à l'aide d'un empilement de 7 cubes.
On observe que le solide comporte deux étages et que tout cube de l'étage supérieur doit reposer sur un cube à l'étage inférieur.
La vue de dessus permet d'affirmer que l'on utilise 6 cubes à l'étage inférieur.
La vue de droite permet de dire qu'il y a au moins un cube à l'étage supérieur, à la troisième rangée à partir de l'avant.
La vue de dessus montre qu'il n'y a qu'un seul cube à la troisième rangée à partir de l'avant, à l'étage inférieur ; donc il ne peut y avoir qu'un seul cube à la troisième rangée, à l'étage supérieur.
On observe que le solide comporte deux étages et que tout cube de l'étage supérieur doit reposer sur un cube à l'étage inférieur.
La vue de dessus permet d'affirmer que l'on utilise 6 cubes à l'étage inférieur.
La vue de droite permet de dire qu'il y a au moins un cube à l'étage supérieur, à la troisième rangée à partir de l'avant.
La vue de dessus montre qu'il n'y a qu'un seul cube à la troisième rangée à partir de l'avant, à l'étage inférieur ; donc il ne peut y avoir qu'un seul cube à la troisième rangée, à l'étage supérieur.
Par conséquent, le solide est réalisé avec 7 (= 6 + 1) cubes.
Nous donnons ci-dessous une représentation en perspective de l'édifice.
Nous donnons ci-dessous une représentation en perspective de l'édifice.
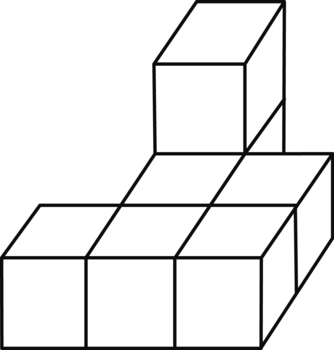 |
Remarque : La vue de face n'est pas nécessaire à la résolution de l'exercice, les vues de dessus et de droite suffisent.
L'affirmation 5 est vraie.
L'affirmation 5 est vraie.
6. Affirmation 6 : En insérant de différentes manières exactement deux parenthèses dans l'écriture 8 × 7 + 3 × 5 on peut obtenir tous les nombres de la liste suivante : 71 ; 176 ; 283 ; 295 ; 400.
On passe en revue, de façon systématique, toutes les positions possibles pour les parenthèses… certains résultats sont redondants à cause des priorités opératoires, qui agissent comme des parenthèses non écrites.
(8 × 7) + 3 × 5 = 71
(8 × 7 + 3) × 5 = 295
(8 × 7 + 3 × 5) = 71
8 × (7 + 3 × 5) = 176
8 × (7 + 3) × 5 = 400
8 × 7 + (3 × 5) = 71
Nous avons effectué les calculs pour toutes les positions possibles des parenthèses, sans obtenir la valeur 283.
L'affirmation 6 est fausse.
On passe en revue, de façon systématique, toutes les positions possibles pour les parenthèses… certains résultats sont redondants à cause des priorités opératoires, qui agissent comme des parenthèses non écrites.
(8 × 7) + 3 × 5 = 71
(8 × 7 + 3) × 5 = 295
(8 × 7 + 3 × 5) = 71
8 × (7 + 3 × 5) = 176
8 × (7 + 3) × 5 = 400
8 × 7 + (3 × 5) = 71
Nous avons effectué les calculs pour toutes les positions possibles des parenthèses, sans obtenir la valeur 283.
L'affirmation 6 est fausse.
Exercice 2 (5 points)
Partie A :
1.
Aire f du rectangle AFED
f(x) = AD × DE
On sait que : AD = x. Par ailleurs, comme ABC est rectangle isocèle en A, on a :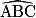 = 45°. Comme D
= 45°. Comme D  [AB] et E
[AB] et E  [BC], on a donc :
[BC], on a donc : 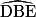 = 45°. De plus
= 45°. De plus  = 90°, le triangle DBE est donc rectangle isocèle en D. On en déduit que : DE = DB = (AB − AD) = 1 − x.
= 90°, le triangle DBE est donc rectangle isocèle en D. On en déduit que : DE = DB = (AB − AD) = 1 − x.
Finalement, f(x) = AD × DE = x(1 − x) = −x2 + x.
On sait que : AD = x. Par ailleurs, comme ABC est rectangle isocèle en A, on a :
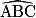 = 45°. Comme D
= 45°. Comme D  [AB] et E
[AB] et E  [BC], on a donc :
[BC], on a donc : 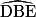 = 45°. De plus
= 45°. De plus  = 90°, le triangle DBE est donc rectangle isocèle en D. On en déduit que : DE = DB = (AB − AD) = 1 − x.
= 90°, le triangle DBE est donc rectangle isocèle en D. On en déduit que : DE = DB = (AB − AD) = 1 − x.Finalement, f(x) = AD × DE = x(1 − x) = −x2 + x.
2. a) Formule pour la cellule B2
On peut taper : « B2=−A2*A2+A2 » ou : « B2=−A2(accent circonflexe)2+A2 ».
On peut taper : « B2=−A2*A2+A2 » ou : « B2=−A2(accent circonflexe)2+A2 ».
b) Maximum pour f
La lecture seule du tableau ne permet pas de conclure.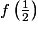 est la valeur maximale parmi les valeurs présentes dans le tableau, mais on ne sait pas quelles sont les valeurs prises entre les valeurs fournies par le tableau.
est la valeur maximale parmi les valeurs présentes dans le tableau, mais on ne sait pas quelles sont les valeurs prises entre les valeurs fournies par le tableau.
La lecture seule du tableau ne permet pas de conclure.
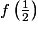 est la valeur maximale parmi les valeurs présentes dans le tableau, mais on ne sait pas quelles sont les valeurs prises entre les valeurs fournies par le tableau.
est la valeur maximale parmi les valeurs présentes dans le tableau, mais on ne sait pas quelles sont les valeurs prises entre les valeurs fournies par le tableau.3. a) Montrons que : f(x) = 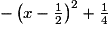 .
.
Lorsqu'il s'agit de démontrer une égalité, on part de la forme la plus factorisée pour essayer d'obtenir, par développement, la forme simplifiée. Si les deux membres de l'égalité sont complexes, on les simplifie séparément pour obtenir la même forme simplifiée.
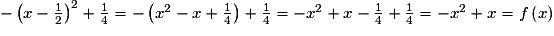 d'après 1.
d'après 1.
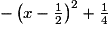 .
.Lorsqu'il s'agit de démontrer une égalité, on part de la forme la plus factorisée pour essayer d'obtenir, par développement, la forme simplifiée. Si les deux membres de l'égalité sont complexes, on les simplifie séparément pour obtenir la même forme simplifiée.
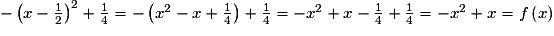 d'après 1.
d'après 1.b) On en déduit l'aire maximale.
On observe que l'expression :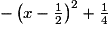 est constituée d'un terme négatif :
est constituée d'un terme négatif : 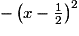 , variable, et d'un terme constant et positif :
, variable, et d'un terme constant et positif : 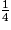 . Cette expression atteint donc sa valeur maximale lorsque le terme négatif est maximal, c'est-à-dire ici, égal à zéro.
. Cette expression atteint donc sa valeur maximale lorsque le terme négatif est maximal, c'est-à-dire ici, égal à zéro.
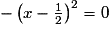 si et seulement si x =
si et seulement si x = 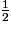 . On a alors :
. On a alors : 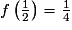 .
.
L'aire maximale est donc 0,25 m2 ; elle est atteinte pour x = 0,5 m.
On observe que l'expression :
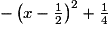 est constituée d'un terme négatif :
est constituée d'un terme négatif : 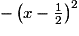 , variable, et d'un terme constant et positif :
, variable, et d'un terme constant et positif : 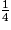 . Cette expression atteint donc sa valeur maximale lorsque le terme négatif est maximal, c'est-à-dire ici, égal à zéro.
. Cette expression atteint donc sa valeur maximale lorsque le terme négatif est maximal, c'est-à-dire ici, égal à zéro.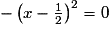 si et seulement si x =
si et seulement si x = 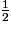 . On a alors :
. On a alors : 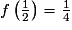 .
.L'aire maximale est donc 0,25 m2 ; elle est atteinte pour x = 0,5 m.
c) Nature du rectangle d'aire maximale
Lorsque x = AD = 0,5 on a DE = (AB − AD) = 1 − 0,5 = 0,5.
Le rectangle ADEF a donc deux côtés consécutifs de même longueur, c'est donc un carré.
Lorsque x = AD = 0,5 on a DE = (AB − AD) = 1 − 0,5 = 0,5.
Le rectangle ADEF a donc deux côtés consécutifs de même longueur, c'est donc un carré.
Partie B :
1.
Intervalle de définition de x
Comme G  [BC] et que x = BG, on a : 0
[BC] et que x = BG, on a : 0  x
x  BG. Or BG est l'hypoténuse du triangle ABC, rectangle et isocèle en A et de côté AB = 1. On a donc BC =
BG. Or BG est l'hypoténuse du triangle ABC, rectangle et isocèle en A et de côté AB = 1. On a donc BC = 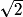 (ce résultat peut être établi à l'aide du théorème de Pythagore, s'il n'est pas mémorisé).
(ce résultat peut être établi à l'aide du théorème de Pythagore, s'il n'est pas mémorisé).
x se trouve donc dans l'intervalle I = [0 ;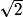 ].
].
 [BC] et que x = BG, on a : 0
[BC] et que x = BG, on a : 0  x
x  BG. Or BG est l'hypoténuse du triangle ABC, rectangle et isocèle en A et de côté AB = 1. On a donc BC =
BG. Or BG est l'hypoténuse du triangle ABC, rectangle et isocèle en A et de côté AB = 1. On a donc BC = 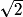 (ce résultat peut être établi à l'aide du théorème de Pythagore, s'il n'est pas mémorisé).
(ce résultat peut être établi à l'aide du théorème de Pythagore, s'il n'est pas mémorisé).x se trouve donc dans l'intervalle I = [0 ;
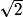 ].
].2.
Expression de g(x)
1ère méthode
L'aire du rectangle DEFG est donnée par la formule : g(x) = DE × DG.
Il s'agit d'exprimer DE et DG en fonction de x.
Par un raisonnement analogue à celui mené en A. 1., on montre que le triangle BGD est rectangle et isocèle en G. Par conséquent, DG = BG = x.
Par ailleurs, comme les droites (DE) et (BC) sont parallèles et que les droites (BD) et (EC) sont sécantes en A, on a, d'après le théorème de Thalès :
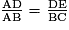 (1).
(1).
Or, AD = AB − BD car D [AB], AB = 1 et BC =
[AB], AB = 1 et BC = 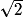 .
.
De plus, dans le riangle BGD, rectangle en G, on a, d'après le théorème de Pythagore : BG2 + GD2 = BD2 d'où : BD2 = 2x2 et BD =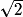 x.
x.
Finalement, (1) s'écrit :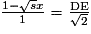 et donc DE =
et donc DE = 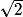 − 2x.
− 2x.
On peut à présent écrire : g(x) = DE × DG = (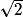 − 2x) × x.
− 2x) × x.
L'aire du rectangle DEFG est donnée par la formule : g(x) = DE × DG.
Il s'agit d'exprimer DE et DG en fonction de x.
Par un raisonnement analogue à celui mené en A. 1., on montre que le triangle BGD est rectangle et isocèle en G. Par conséquent, DG = BG = x.
Par ailleurs, comme les droites (DE) et (BC) sont parallèles et que les droites (BD) et (EC) sont sécantes en A, on a, d'après le théorème de Thalès :
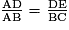 (1).
(1).Or, AD = AB − BD car D
 [AB], AB = 1 et BC =
[AB], AB = 1 et BC = 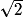 .
.De plus, dans le riangle BGD, rectangle en G, on a, d'après le théorème de Pythagore : BG2 + GD2 = BD2 d'où : BD2 = 2x2 et BD =
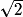 x.
x.Finalement, (1) s'écrit :
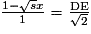 et donc DE =
et donc DE = 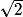 − 2x.
− 2x.On peut à présent écrire : g(x) = DE × DG = (
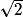 − 2x) × x.
− 2x) × x.2e méthode
L'aire du rectangle peut s'écrire :
g(x) = AABC − AADE − ABGD − AEFC =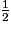 × (AB × AC − AD × AE − BG × GD − FE × FC)
× (AB × AC − AD × AE − BG × GD − FE × FC)
Par un raisonnement analogue à celui mené en A. 1., on montre que les triangles BGD (resp. EFC) sont rectangles et isocèles en G (resp. en F). Par conséquent, DG = BG = x et FE = FC = x.
Les triangles BGD et EFC étant isométriques (superposables), on a aussi : BD = EC, d'où l'on déduit que AD = AE car AD = AB − BD = AC − EC.
De plus, dans le triangle BGD, rectangle en G, on a, d'après le théorème de Pythagore : BG2 + GD2 = BD2 d'où : BD2 = 2x2 et BD =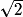 x.
x.
Doù AD = AE = 1−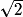 x.
x.
Finalement, g(x) =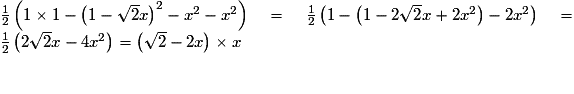 .
.
L'aire du rectangle peut s'écrire :
g(x) = AABC − AADE − ABGD − AEFC =
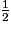 × (AB × AC − AD × AE − BG × GD − FE × FC)
× (AB × AC − AD × AE − BG × GD − FE × FC)Par un raisonnement analogue à celui mené en A. 1., on montre que les triangles BGD (resp. EFC) sont rectangles et isocèles en G (resp. en F). Par conséquent, DG = BG = x et FE = FC = x.
Les triangles BGD et EFC étant isométriques (superposables), on a aussi : BD = EC, d'où l'on déduit que AD = AE car AD = AB − BD = AC − EC.
De plus, dans le triangle BGD, rectangle en G, on a, d'après le théorème de Pythagore : BG2 + GD2 = BD2 d'où : BD2 = 2x2 et BD =
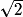 x.
x.Doù AD = AE = 1−
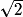 x.
x.Finalement, g(x) =
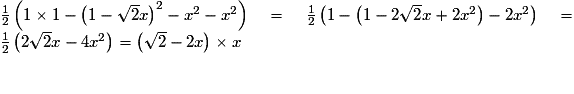 .
.3. a) Sur le graphique, on lit que y = 0,2 pour x = 0,2 ou x = 0,51. Ces deux solutions sont compatibles avec les données du problème. Les positions de G telles que BG = 0,2 ou BG = 0,5 correspondent à des rectangles GDEF d'aire 0,2 m2.
b)
Par lecture graphique, on a : Airemax = 0,25 m2.
c) DEFG est un carré lorsque DG = DE, c'est-à-dire lorsque x = 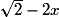 , soit : x =
, soit : x = 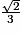 .
.
Or g(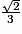 ) = −2
) = −2 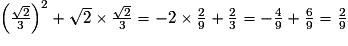
<0,25
L'aire n'est donc pas maximale lorsque DEFG est un carré.
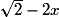 , soit : x =
, soit : x = 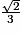 .
.Or g(
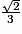 ) = −2
) = −2 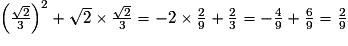
<0,25
L'aire n'est donc pas maximale lorsque DEFG est un carré.
Exercice 3 (2 points)
La résolution de l'exercice repose sur la connaissance (supposée) de la part des candidats des critères de divisibilité par 11 et 3.
1. Valeurs de n pour lesquelles An est divisible par 11
An est divisible par 11 si et seulement si la différence D entre la somme de ses chiffres de rangs pairs et la somme de ses chiffres de rangs impairs est divisible par 11.
Ici, tous les chiffres sont égaux à 1 ; on voit donc qu'il y a deux cas de figure possibles :
An est divisible par 11 si et seulement si la différence D entre la somme de ses chiffres de rangs pairs et la somme de ses chiffres de rangs impairs est divisible par 11.
Ici, tous les chiffres sont égaux à 1 ; on voit donc qu'il y a deux cas de figure possibles :
- soit n est pair et il y a autant de chiffres de rangs pairs que de chiffres de rangs impairs, et alors D = 0 qui est divisible par 11 ;
- soit n est impair et il y a un chiffre de rang impair de plus que de chiffres de rangs pairs, et alors D = 1, qui n'est pas divisible par 11.
2. Valeurs de n pour lesquelles An est divisible par 33
33 = 3 × 11 et 3 et 11 sont premiers entre eux ; par conséquent, An est divisible par 33 si et seulement si An est divisible par 11 et par 3.
Nous avons vu ci-dessus que An est divisible par 11 si et seulement si n est pair ; pour que An soit de plus divisible par 3, il faut et il suffit que la somme de ses chiffres soit divisible par 3. La somme des chiffres de An est : n.
Conclusion : An est divisible par 33 si et seulement si n est pair et divisible par 3 (autrement dit : n est multiple de 6).
33 = 3 × 11 et 3 et 11 sont premiers entre eux ; par conséquent, An est divisible par 33 si et seulement si An est divisible par 11 et par 3.
Nous avons vu ci-dessus que An est divisible par 11 si et seulement si n est pair ; pour que An soit de plus divisible par 3, il faut et il suffit que la somme de ses chiffres soit divisible par 3. La somme des chiffres de An est : n.
Conclusion : An est divisible par 33 si et seulement si n est pair et divisible par 3 (autrement dit : n est multiple de 6).
