Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (5 points)
Dans cet exercice, six affirmations sont proposées. Pour chacune, préciser si elle est vraie ou fausse, et justifier la réponse.
Une réponse exacte mais non justifiée ne rapporte aucun point.
1. Dans une salle, 9 personnes sont assises, leur moyenne d'âge est de 25 ans. Dans une autre salle, 11 personnes sont réunies, leur moyenne d'âge est de 45 ans. On rassemble les deux groupes de personnes.
Affirmation 1 : « la moyenne d'âge du groupe ainsi constitué est de 35 ans ».
Affirmation 1 : « la moyenne d'âge du groupe ainsi constitué est de 35 ans ».
2. Maxime possède 3 pantalons (un rouge, un bleu et un noir) et 4 tee-shirts (un rouge, un bleu, un jaune et un vert). Il choisit au hasard un pantalon puis un tee-shirt. (On admet que les choix sont équiprobables.)
Affirmation 2 : « la probabilité qu'il soit habillé d'une seule couleur est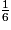 ».
».
Affirmation 2 : « la probabilité qu'il soit habillé d'une seule couleur est
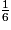 ».
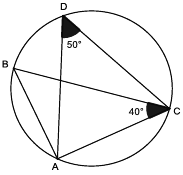
».3. Affirmation 3 : « le triangle ABC représenté ci-contre est rectangle en A ».
 |
4. Affirmation 4 : « la section d'un cylindre de rayon 5 cm et de hauteur 8 cm par un plan parallèle à son axe peut être un carré ».
5. Une cuve a deux robinets de vidange A et B.
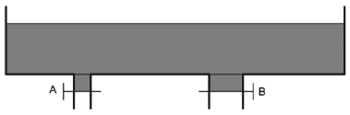 |
Si on ouvre seulement le robinet A, la cuve pleine se vide en 7 heures.
Si on ouvre seulement le robinet B, la cuve pleine se vide en 3 heures.
On ouvre les deux robinets A et B en même temps.
Affirmation 5 : « la cuve pleine se vide en 2 heures et 6 minutes ».
Si on ouvre seulement le robinet B, la cuve pleine se vide en 3 heures.
On ouvre les deux robinets A et B en même temps.
Affirmation 5 : « la cuve pleine se vide en 2 heures et 6 minutes ».
6. On considère la carafe sphérique représentée ci-dessous.
On s'intéresse au volume de liquide V contenu dans la carafe pour une hauteur h de remplissage.
On s'intéresse au volume de liquide V contenu dans la carafe pour une hauteur h de remplissage.
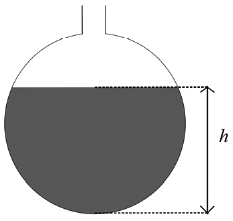 |
Affirmation 6 : « le graphique ci-contre représente V en fonction de h ».
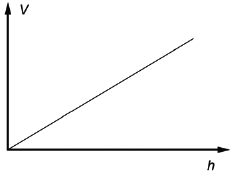 |
Exercice 2 (4 points)
Les questions 2. et 3. sont indépendantes.
1. Soit ABCD un carré de centre M. On admet l'existence des points E, F, G et H tels que :
Dans la suite de l'exercice, la longueur AB est quelconque.
- E est le point de la demi-droite [MC) tel que BDE est un triangle équilatéral ;
- F est le point symétrique du point M par rapport au point C ;
- G est le point tel que MDGE est un rectangle ;
- H est le point tel que MDHF est un rectangle.
Dans la suite de l'exercice, la longueur AB est quelconque.
2. a) Justifier que l'aire du rectangle MDGE est égale à l'aire du triangle BDE.
2. b) Justifier que l'aire du rectangle MDHF est égale à l'aire du carré ABCD.
2. c) En déduire que l'aire du carré ABCD est supérieure à l'aire du triangle BDE.
3.
On pose AB = c.
3. a) Exprimer l'aire du triangle BDE en fonction de c.
3. b) Retrouver le résultat de la question 2. c).
4. Déterminer le point P de la demi-droite [MC) tel que l'aire du triangle BDP soit égale à l'aire du carré ABCD.
Exercice 3 (3 points)
Un critère de divisibilité par 4 est le suivant : « soit n un nombre entier naturel ayant au moins deux chiffres. n est divisible par 4 si et seulement si le nombre composé de ses deux derniers chiffres est divisible par 4 ».
1. Le nombre 123 412 893 135 552 est-il divisible par 4 ?
2.
L'objet de cette question est de démontrer le critère.
On considère un nombre entier naturel n ayant au moins deux chiffres.
On considère un nombre entier naturel n ayant au moins deux chiffres.
2. a) Justifier que l'on peut écrire n sous la forme n = 100q + r, où q et r sont des nombres entiers naturels et 0  r < 100.
r < 100.
 r < 100.
r < 100.2. b) Démontrer que si r est divisible par 4, alors n est divisible par 4.
2. c) Démontrer que si n est divisible par 4, alors r est divisible par 4.
2. d) En déduire une démonstration du critère de divisibilité par 4.
3. a) Quel peut être un critère de divisibilité par 8 pour les nombres entiers naturels ayant au moins trois chiffres ? Justifier brièvement.
3. b) Le nombre 123 412 893 135 552 est-il divisible par 8 ?
4. a) En généralisant, quel critère de divisibilité concernant les nombres entiers naturels ayant au moins p chiffres (p  1) peut-on formuler ? Démontrer.
1) peut-on formuler ? Démontrer.
 1) peut-on formuler ? Démontrer.
1) peut-on formuler ? Démontrer.4. b) Quelle est la plus grande puissance de 2 qui divise le nombre 123 412 893 135 552 ?
Corrigé
Corrigé
Exercice 1
Dans la plupart des exercices de type « vrai ou faux », les justifications prennent deux formes :
- dans le cas où la proposition est fausse, il suffit de fournir un contre-exemple ;
- dans le cas où la proposition est vraie, il faut argumenter en invoquant des propriétés connues.
1. Propriété : La moyenne d'une série statistique (x1,x2,…xn) s'obtient en effectuant le quotient :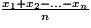 .
.
Dans la première salle, il y a 9 personnes, dont la moyenne d'âge est 25 ans. Le total des âges de ces 9 personnes est donc : 25 × 9 = 225 ans.
Dans la deuxième salle, il y a 11 personnes, dont la moyenne d'âge est 45 ans. Le total des âges de ces 11 personnes est donc : 45 × 11 = 495 ans.
En rassemblant tout le monde, on obtient un groupe de 20 personnes, dont le total des âges est : 495 + 225 = 720 ans.
La moyenne d'âge du groupe est alors :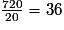 ans.
ans.
L'affirmation 1 est fausse.
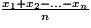 .
.Dans la première salle, il y a 9 personnes, dont la moyenne d'âge est 25 ans. Le total des âges de ces 9 personnes est donc : 25 × 9 = 225 ans.
Dans la deuxième salle, il y a 11 personnes, dont la moyenne d'âge est 45 ans. Le total des âges de ces 11 personnes est donc : 45 × 11 = 495 ans.
En rassemblant tout le monde, on obtient un groupe de 20 personnes, dont le total des âges est : 495 + 225 = 720 ans.
La moyenne d'âge du groupe est alors :
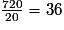 ans.
ans.L'affirmation 1 est fausse.
2. Propriété : Lorsque des issues sont équiprobables, la probabilité d'un événement est égale au quotient : (nombre d'issues favorables à l'événement considéré)/(nombre total d'issues possibles lors de l'expérience).
Avec 3 pantalons et 4 tee-shirts, on peut produire 2 × 4 = 12 tenues différentes.
Parmi ces douze tenues, il y en a deux qui sont unicolores, à savoir les combinaisons :
« T-shirt rouge - pantalon rouge » et « T-shirt bleu - pantalon bleu ».
La probabilité d'être habillé d'une seule couleur est donc :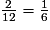 .
.
L'affirmation 2 est vraie.
Avec 3 pantalons et 4 tee-shirts, on peut produire 2 × 4 = 12 tenues différentes.
Parmi ces douze tenues, il y en a deux qui sont unicolores, à savoir les combinaisons :
« T-shirt rouge - pantalon rouge » et « T-shirt bleu - pantalon bleu ».
La probabilité d'être habillé d'une seule couleur est donc :
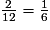 .
.L'affirmation 2 est vraie.
3. Propriété : Dans un cercle, la mesure d'un angle au centre est égale au double de la mesure de tout angle inscrit interceptant le même arc.
Conséquence : Deux angles inscrits dans un cercle, qui interceptent le même arc, ont la même mesure.
Les points A, B, C et D sont cocycliques (ils sont sur le même cercle) et les angles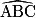 et
et 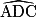 interceptent le même arc 'AC. D'après la propriété évoquée ci-dessus, on en déduit que les angles
interceptent le même arc 'AC. D'après la propriété évoquée ci-dessus, on en déduit que les angles 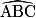 et
et 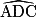 sont égaux et donc que :
sont égaux et donc que : 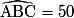 °.
°.
La somme des mesures des angles du triangle ABC vaut 180°. Comme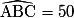 ° et
° et 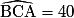 °, on en déduit que :
°, on en déduit que :
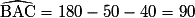 °.
°.
L'affirmation 3 est vraie.
Conséquence : Deux angles inscrits dans un cercle, qui interceptent le même arc, ont la même mesure.
Les points A, B, C et D sont cocycliques (ils sont sur le même cercle) et les angles
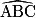 et
et 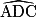 interceptent le même arc 'AC. D'après la propriété évoquée ci-dessus, on en déduit que les angles
interceptent le même arc 'AC. D'après la propriété évoquée ci-dessus, on en déduit que les angles 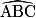 et
et 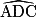 sont égaux et donc que :
sont égaux et donc que : 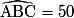 °.
°.La somme des mesures des angles du triangle ABC vaut 180°. Comme
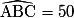 ° et
° et 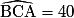 °, on en déduit que :
°, on en déduit que :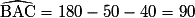 °.
°.L'affirmation 3 est vraie.
 |
4. Propriété : La section d'un cylindre de rayon R et de hauteur h par un plan parallèle à son axe est un rectangle de dimensions : h et l, avec 0  l
l  R.
R.
La section du cylindre considéré sera donc un rectangle dont une dimension est : 8 cm et dont l'autre dimension est inférieure ou égale à 10 cm. Les deux dimensions peuvent donc être égales et la section peut être un carré de côté 8 cm.
L'affirmation 4 est vraie.
 l
l  R.
R.La section du cylindre considéré sera donc un rectangle dont une dimension est : 8 cm et dont l'autre dimension est inférieure ou égale à 10 cm. Les deux dimensions peuvent donc être égales et la section peut être un carré de côté 8 cm.
L'affirmation 4 est vraie.
5. Il s'agit dans un premier temps d'un problème de proportionnalité, puis de conversion d'unités de mesure de la durée.
En une heure, le robinet A permet de vider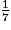 de la cuve et dans le même temps (une heure), le robinet B permet de vider
de la cuve et dans le même temps (une heure), le robinet B permet de vider 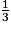 de la cuve.
de la cuve.
Lorsque l'on ouvre les deux robinets, on pourra vider en une heure :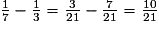 de la cuve.
de la cuve.
Si en une heure on vide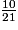 de la cuve, on mettra
de la cuve, on mettra 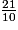 d'heure à vider la cuve entière.
d'heure à vider la cuve entière.
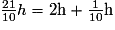 et
et 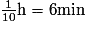 car 1 h = 60 min.
car 1 h = 60 min.
La durée de vidage est donc : 2 h 6 min.
L'affirmation 5 est vraie.
En une heure, le robinet A permet de vider
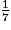 de la cuve et dans le même temps (une heure), le robinet B permet de vider
de la cuve et dans le même temps (une heure), le robinet B permet de vider 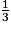 de la cuve.
de la cuve.Lorsque l'on ouvre les deux robinets, on pourra vider en une heure :
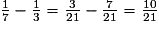 de la cuve.
de la cuve.Si en une heure on vide
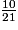 de la cuve, on mettra
de la cuve, on mettra 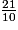 d'heure à vider la cuve entière.
d'heure à vider la cuve entière.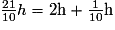 et
et 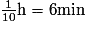 car 1 h = 60 min.
car 1 h = 60 min.La durée de vidage est donc : 2 h 6 min.
L'affirmation 5 est vraie.
6. Le graphique proposé est une droite passant par l'origine, ce qui signifie que V est proportionnel à h. Or le volume de liquide contenu dans une carafe sphérique n'est pas proportionnel à la hauteur de remplissage : 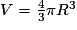 R étant le rayon de la sphère.
R étant le rayon de la sphère.
Remarque : à défaut de connaître la formule du volume d'une sphère, les seuls arguments pouvant être invoqués par le candidat sont « de bon sens » : le niveau d'eau « monte plus vite » dans un récipient sphérique, selon que l'on complète le remplissage à partir du fond (ou très près du haut) ou autour de la mi-hauteur du récipient…
L'affirmation 6 est donc fausse.
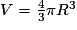 R étant le rayon de la sphère.
R étant le rayon de la sphère.Remarque : à défaut de connaître la formule du volume d'une sphère, les seuls arguments pouvant être invoqués par le candidat sont « de bon sens » : le niveau d'eau « monte plus vite » dans un récipient sphérique, selon que l'on complète le remplissage à partir du fond (ou très près du haut) ou autour de la mi-hauteur du récipient…
L'affirmation 6 est donc fausse.
Exercice 2
1.
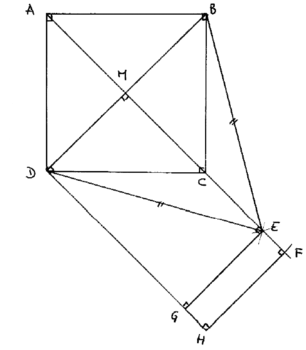 |
BE = ED = BD
AB = BC = CD = DA = 6 cm
AB = BC = CD = DA = 6 cm
2. Les formules d'aires à connaître ici sont :
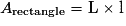 où L et l sont respectivement la longueur et la largeur du rectangle ;
où L et l sont respectivement la longueur et la largeur du rectangle ;
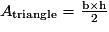 où b est la longueur d'une base (d'un côté) du triangle et h la hauteur relative à cette base.
où b est la longueur d'une base (d'un côté) du triangle et h la hauteur relative à cette base.
Il est donc possible d'écrire trois formules d'aire pour chaque triangle, selon que l'on considère l'un ou l'autre ou encore le troisième de ses côtés comme base. Les données de l'énoncé poussent habituellement à privilégier l'une des trois formules…
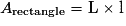 où L et l sont respectivement la longueur et la largeur du rectangle ;
où L et l sont respectivement la longueur et la largeur du rectangle ;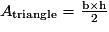 où b est la longueur d'une base (d'un côté) du triangle et h la hauteur relative à cette base.
où b est la longueur d'une base (d'un côté) du triangle et h la hauteur relative à cette base.Il est donc possible d'écrire trois formules d'aire pour chaque triangle, selon que l'on considère l'un ou l'autre ou encore le troisième de ses côtés comme base. Les données de l'énoncé poussent habituellement à privilégier l'une des trois formules…
2. a) 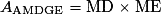 car MDGE est un rectangle.
car MDGE est un rectangle.
Par ailleurs, on sait que M est le milieu du segment [BD] car M est le centre du carré ABCD. (EM) est donc la médiane issue de E dans le triangle BDE. Or le triangle BDE est équilatéral, donc la médiane (EM) est aussi la hauteur issue de E. La base correspondant à cette hauteur est : [BD].
On a donc :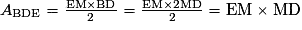 .
.
L'aire du triangle BDE est donc égale à l'aire du rectangle MDGE.
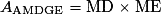 car MDGE est un rectangle.
car MDGE est un rectangle.Par ailleurs, on sait que M est le milieu du segment [BD] car M est le centre du carré ABCD. (EM) est donc la médiane issue de E dans le triangle BDE. Or le triangle BDE est équilatéral, donc la médiane (EM) est aussi la hauteur issue de E. La base correspondant à cette hauteur est : [BD].
On a donc :
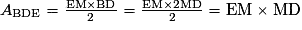 .
.L'aire du triangle BDE est donc égale à l'aire du rectangle MDGE.
2. b) 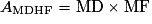 .
.
Or F est le symétrique de M par rapport à C, C est donc le milieu de [MF] et MF = 2MC.
D'où, finalement :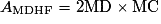 .
.
M est le centre du carré ABCD, les triangles AMB, BMC, CMD et DMA sont donc superposables et rectangles en M. On en déduit que :
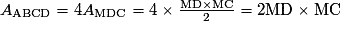 .
.
L'aire du rectangle MDHF est donc égale à l'aire du carré ABCD.
Remarque : on pouvait également calculer l'aire du carré ABCD de façon plus classique en donnant : AABCD = AB2.
Or MD et MC sont des demi-diagonales du carré ABCD, d'où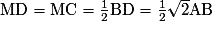 .
.
On en déduit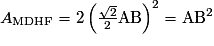 , d'où le résultat.
, d'où le résultat.
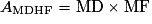 .
.Or F est le symétrique de M par rapport à C, C est donc le milieu de [MF] et MF = 2MC.
D'où, finalement :
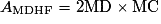 .
.M est le centre du carré ABCD, les triangles AMB, BMC, CMD et DMA sont donc superposables et rectangles en M. On en déduit que :
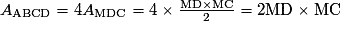 .
.L'aire du rectangle MDHF est donc égale à l'aire du carré ABCD.
Remarque : on pouvait également calculer l'aire du carré ABCD de façon plus classique en donnant : AABCD = AB2.
Or MD et MC sont des demi-diagonales du carré ABCD, d'où
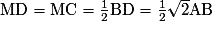 .
.On en déduit
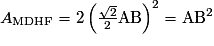 , d'où le résultat.
, d'où le résultat.2. c) Pour montrer que l'aire du carré ABCD est supérieure à l'aire du triangle BDE, il suffit de montrer que l'aire du rectangle MDHF est supérieure à l'aire du rectangle MDGE, d'après les questions 2 a) et 2 b).
Les rectangles MDHF et MDGE ont un côté commun : MD. Pour comparer leurs aires, il suffit donc de comparer les longueurs ME et MF.
Le triangle DME est rectangle en M. On en déduit que : DE > ME. (1)
Or MF = 2MC (car F est le symétrique de M par rapport à C) ;
= AC (car M est le milieu de [AC]) ;
= DB (car DB et AC sont les diagonales du carré ABCD et sont donc de même longueur) ;
= DE (car le triangle BDE est équilatéral).
On déduit de (1) que : MF > ME et donc que le rectangle MDHF a une aire supérieure à celle du rectangle MDGE.
Conclusion : l'aire du carré ABCD est supérieure à l'aire du triangle BDE.
Les rectangles MDHF et MDGE ont un côté commun : MD. Pour comparer leurs aires, il suffit donc de comparer les longueurs ME et MF.
Le triangle DME est rectangle en M. On en déduit que : DE > ME. (1)
Or MF = 2MC (car F est le symétrique de M par rapport à C) ;
= AC (car M est le milieu de [AC]) ;
= DB (car DB et AC sont les diagonales du carré ABCD et sont donc de même longueur) ;
= DE (car le triangle BDE est équilatéral).
On déduit de (1) que : MF > ME et donc que le rectangle MDHF a une aire supérieure à celle du rectangle MDGE.
Conclusion : l'aire du carré ABCD est supérieure à l'aire du triangle BDE.
3. Soit AB = c.
3. a) Exprimons ABDE en fonction de c.
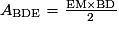 et
et 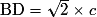 , car BD est une diagonale du carré ABCD, de côté c.
, car BD est une diagonale du carré ABCD, de côté c.
Calculons EM.
Dans le triangle MED, rectangle en M, on a, d'après le théorème de Pythagore :
DM2 + ME2 = DE2. Or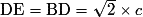 et
et 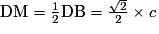 .
.
On en déduit que :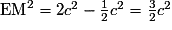 et
et 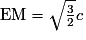 .
.
Finalement,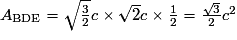 .
.
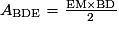 et
et 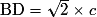 , car BD est une diagonale du carré ABCD, de côté c.
, car BD est une diagonale du carré ABCD, de côté c.Calculons EM.
Dans le triangle MED, rectangle en M, on a, d'après le théorème de Pythagore :
DM2 + ME2 = DE2. Or
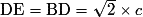 et
et 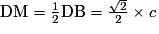 .
.On en déduit que :
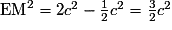 et
et 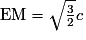 .
.Finalement,
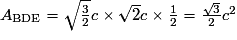 .
.3. b) 3 < 4 donc 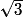 < 2 et
< 2 et 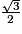 < 1.
< 1.
Par conséquent,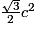 < c2 et donc l'aire du triangle BDE est inférieure à celle du carré ABCD, ce qui a déjà été prouvé à la question 2 c).
< c2 et donc l'aire du triangle BDE est inférieure à celle du carré ABCD, ce qui a déjà été prouvé à la question 2 c).
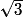 < 2 et
< 2 et 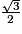 < 1.
< 1.Par conséquent,
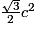 < c2 et donc l'aire du triangle BDE est inférieure à celle du carré ABCD, ce qui a déjà été prouvé à la question 2 c).
< c2 et donc l'aire du triangle BDE est inférieure à celle du carré ABCD, ce qui a déjà été prouvé à la question 2 c).4. Considérons un point P quelconque sur la demi-droite [MC). Comme M est le milieu de [BD] et comme la demi-droite [MC) est perpendiculaire à la droite (DB), la droite (MP) est la hauteur issue de P dans le triangle BDP.
Par conséquent, l'aire du triangle BPD est égale à :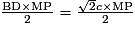 .
.
Pour que cette aire soit égale à l'aire du carré ABCD, soit c2, il faut que : MP =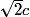 = AC = 2MC, ce qui revient à dire que P et F doivent être confondus.
= AC = 2MC, ce qui revient à dire que P et F doivent être confondus.
Conclusion : F est le point de la demi-droite [MC) tel que l'aire du triangle BDF soit égale à celle du carré ABCD.
Par conséquent, l'aire du triangle BPD est égale à :
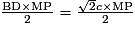 .
.Pour que cette aire soit égale à l'aire du carré ABCD, soit c2, il faut que : MP =
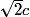 = AC = 2MC, ce qui revient à dire que P et F doivent être confondus.
= AC = 2MC, ce qui revient à dire que P et F doivent être confondus.Conclusion : F est le point de la demi-droite [MC) tel que l'aire du triangle BDF soit égale à celle du carré ABCD.
Exercice 3
1. 52 = 13 × 4 donc 52 est divisible par 4. On en déduit que 123 412 893 135 552 est divisible par 4.
2. a) La division euclidienne de n par 100 permet d'écrire que : n = 100q + r avec q entier naturel et 0  r < 100.
r < 100.
La démonstration des questions b) et c) repose sur la propriété suivante : « lorsque deux nombres sont divisibles par un même entier, alors leur somme et leur différence est également divisible par cet entier ».
 r < 100.
r < 100.La démonstration des questions b) et c) repose sur la propriété suivante : « lorsque deux nombres sont divisibles par un même entier, alors leur somme et leur différence est également divisible par cet entier ».
2. b) 100q = 4 × 25q est divisible par 4. Par conséquent, si r est divisible par 4, alors 100q + r, c'est-à-dire n, l'est.
2. c) Si n est divisible par 4, alors r = n − 100q l'est d'après la propriété ci-dessus.
2. d) La démonstration du critère de divisibilité par 4 découle de ce qui précède (questions b) et c)) après avoir remarqué que r est le nombre composé des deux derniers chiffres de n.
3. a) Tout nombre n peut s'écrire 1000q + r avec q entier naturel et r entier tel que 0  r < 1000.
r < 1000.
1000 = 8 × 25. On établit donc, par un raisonnement analogue à celui qui précède, que n est divisible par 8 si et seulement r l'est. Si n est un nombre d'au moins trois chiffres, alors r est le nombre composé de ses trois derniers chiffres. Le critère de divisibilité par 8 est donc le suivant : « soit n un nombre entier naturel ayant au moins trois chiffres, n est divisible par 8 si et seulement si le nombre composé de ses trois derniers chiffres l'est. »
 r < 1000.
r < 1000.1000 = 8 × 25. On établit donc, par un raisonnement analogue à celui qui précède, que n est divisible par 8 si et seulement r l'est. Si n est un nombre d'au moins trois chiffres, alors r est le nombre composé de ses trois derniers chiffres. Le critère de divisibilité par 8 est donc le suivant : « soit n un nombre entier naturel ayant au moins trois chiffres, n est divisible par 8 si et seulement si le nombre composé de ses trois derniers chiffres l'est. »
3. b) 552 = 69 × 8. On en déduit que 123 412 893 135 552 est divisible par 8.
4. a) Un entier naturel n ayant au moins p chiffres est divisible par 2p si et seulement si le nombre composé de ses p derniers chiffres est divisible par 2p. Démontrons-le.
Soit n un entier naturel ayant au moins p chiffres. La division euclidienne de n par 10p permet d'écrire que : n = 10p × q + r avec q entier naturel et r entier naturel tel que : 0 r < 10p.
r < 10p.
10p = 2p × 5p donc 10p × q est toujours divisible par 2p. Par conséquent, n est divisible par 2p si et seulement si r l'est.
r étant le reste dans la division euclidienne de n par 2p, r est le nombre composé des p derniers chiffres de n.
Remarque : la formulation des critères de divisibilité de cet exercice exige que l'on tolère d'écrire des nombres r dont le(s) chiffre(s) le plus à gauche soi(en)t 0.
Soit n un entier naturel ayant au moins p chiffres. La division euclidienne de n par 10p permet d'écrire que : n = 10p × q + r avec q entier naturel et r entier naturel tel que : 0
 r < 10p.
r < 10p.10p = 2p × 5p donc 10p × q est toujours divisible par 2p. Par conséquent, n est divisible par 2p si et seulement si r l'est.
r étant le reste dans la division euclidienne de n par 2p, r est le nombre composé des p derniers chiffres de n.
Remarque : la formulation des critères de divisibilité de cet exercice exige que l'on tolère d'écrire des nombres r dont le(s) chiffre(s) le plus à gauche soi(en)t 0.
4. b) 3 135 552 = 24 496 × 128 + 64 et 135 552 = 2 118 × 64.
123 412 893 135 552 est donc divisible par 64 (= 26), mais pas par 128 (= 27).
26 est la plus grande puissance de 2 qui divise 123 412 893 135 552.
123 412 893 135 552 est donc divisible par 64 (= 26), mais pas par 128 (= 27).
26 est la plus grande puissance de 2 qui divise 123 412 893 135 552.
