Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
Dans cet exercice, six affirmations sont proposées. Pour chacune, dire si elle est vraie ou fausse, puis justifier la réponse. Une réponse exacte mais non justifiée ne rapporte aucun point.
1. Un cycliste parcourt 100 km. Pendant les premiers 50 kilomètres, il roule à 25 km/h de moyenne puis, fatigué, à 15 km/h pendant les 50 derniers kilomètres.
Affirmation 1 : sa vitesse moyenne sur l'ensemble du parcours est 20 km/h.
Affirmation 1 : sa vitesse moyenne sur l'ensemble du parcours est 20 km/h.
2. Affirmation 2 : tout nombre entier de trois chiffres dont les chiffres des centaines, dizaines et unités sont les mêmes est divisible par 37.
3. Affirmation 3 : deux nombres entiers impairs sont premiers entre eux.
4. Affirmation 4 : l'inverse de 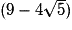 est
est 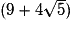 .
.
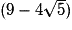 est
est 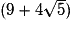 .
.5.
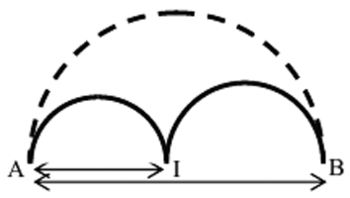
La figure ci-dessous est composée de trois demi-cercles.
Affirmation 5 : la longueur du chemin en trait plein est égale à celle du chemin en pointillés.
Affirmation 5 : la longueur du chemin en trait plein est égale à celle du chemin en pointillés.
 |
6. Dans un laboratoire, on cultive des bactéries. La population de bactéries augmente de 20 % par heure.
Affirmation 6 : la population de bactéries sera multipliée par 2 au bout de 5 heures.
Affirmation 6 : la population de bactéries sera multipliée par 2 au bout de 5 heures.
Exercice 2 (3 points)
On étudie la fonction f qui, à la vitesse v d'un véhicule (exprimée en mètre par seconde) associe la distance de freinage (exprimée en mètre).
Cette fonction est définie par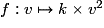 , où k est un coefficient qui dépend notamment de l'état de la route.
, où k est un coefficient qui dépend notamment de l'état de la route.
Cette fonction est définie par
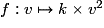 , où k est un coefficient qui dépend notamment de l'état de la route.
, où k est un coefficient qui dépend notamment de l'état de la route.Partie 1
Dans des conditions « normales », lorsque la route est sèche, le coefficient k est égal à 0,08.
1. On utilise un tableur pour créer le tableau de valeurs ci-après :
 |
a) Donner une formule qui, entrée dans la cellule B2 (puis recopiée vers la droite), permet de compléter la ligne 2.
b) On veut qu'en modifiant la valeur de k en B3, les distances soient recalculées automatiquement. La formule proposée au a) satisfait-elle cette nouvelle contrainte ? Si oui, pourquoi ? Si non, en proposer une autre qui convient.
2. a) Calculer la distance de freinage sur route sèche pour une vitesse de 72 km/h.
2. b) À partir de quelle vitesse (arrondie à l'unité, en km/h), la distance de freinage sur route sèche est-elle supérieure à 45 mètres ?
Partie 2
Sur une route mouillée, le coefficient k est différent de 0,08.
Après avoir modifié la valeur de k dans la feuille de calcul précédente, on a construit la représentation graphique qui donne la distance de freinage sur route mouillée en fonction de la vitesse.
Après avoir modifié la valeur de k dans la feuille de calcul précédente, on a construit la représentation graphique qui donne la distance de freinage sur route mouillée en fonction de la vitesse.
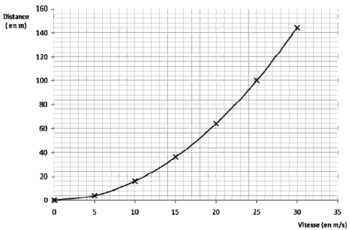 |
1. En utilisant cette représentation graphique, estimer la valeur du coefficient k sur route mouillée.
2. Où se situerait la représentation graphique donnant la distance de freinage sur route sèche en fonction de la vitesse, par rapport à la représentation graphique tracée ? Justifier la réponse par le calcul.
Problème (5 points)
Un polygone régulier est un polygone convexe inscrit dans un cercle et dont tous les côtés ont la même longueur.
Partie A
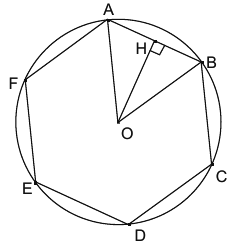
On considère un hexagone régulier ABCDEF inscrit dans un cercle de centre O et de rayon r (voir figure ci-dessous).
H est le pied de la hauteur issue de O, dans le triangle AOB.
H est le pied de la hauteur issue de O, dans le triangle AOB.
 |
Montrer que l'aire de l'hexagone ABCDEF est égale à 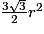 .
.
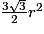 .
.Partie B
Dans cette partie, on pourra utiliser le résultat de la partie A.
On considère un écrou hexagonal en laiton référencé M10. Cette référence signifie que le diamètre de la base du cylindre central est de 10 mm.
La hauteur de l'écrou est égale à 8 mm et la distance entre deux sommets diamétralement opposés de l'hexagone est égale à 18,9 mm (voir schémas ci-après).
On considère un écrou hexagonal en laiton référencé M10. Cette référence signifie que le diamètre de la base du cylindre central est de 10 mm.
La hauteur de l'écrou est égale à 8 mm et la distance entre deux sommets diamétralement opposés de l'hexagone est égale à 18,9 mm (voir schémas ci-après).
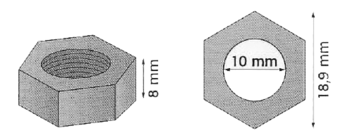 |
Les représentations ne sont pas à l'échelle. L'hexagone est régulier.
On ne prendra pas en compte l'épaisseur du filetage.
On ne prendra pas en compte l'épaisseur du filetage.
1. Déterminer le volume exact de l'écrou, et en donner l'arrondi au millimètre-cube.
2. Sachant que la masse volumique du laiton est 8 400 kg/m3, calculer la masse de l'écrou, arrondie au gramme.
Partie C
RSTUV est un pentagone régulier inscrit dans un cercle de centre O et de rayon r.
1. H est le pied de la hauteur issue de O dans le triangle ROS. Déterminer la longueur OH en fonction de r.
2. Calculer l'aire du pentagone RSTUV en fonction de r.
Corrigé
Corrigé
Exercice 1
Dans la plupart des exercices de type « vrai ou faux », les justifications prennent deux formes :
- dans le cas où la proposition est fausse, il suffit de fournir un contre-exemple ;
- dans le cas où la proposition est vraie, il faut argumenter en invoquant des propriétés connues.
1. Propriété : la vitesse moyenne v d'un objet est donnée par la formule : 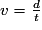 où d est la distance parcourue et t la durée du parcours.
où d est la distance parcourue et t la durée du parcours.
Le cycliste parcourt 100 km, donc d = 100.
Il parcourt les 50 premiers kilomètres en 2h, puisque sa vitesse est alors de 25 km/h.
Les 50 km suivants sont parcourus à la vitesse de 15 km/h ; le parcours dure donc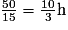 .
.
La vitesse moyenne sur l'ensemble du parcours est donc :
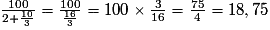 km/h.
km/h.
L'affirmation 1 est fausse.
Remarque : l'affirmation proposée confronte la réflexion à une représentation erronée assez commune, selon laquelle la vitesse moyenne sur un parcours aller-retour, par exemple, est la moyenne de la vitesse à l'aller et de la vitesse au retour.
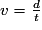 où d est la distance parcourue et t la durée du parcours.
où d est la distance parcourue et t la durée du parcours.Le cycliste parcourt 100 km, donc d = 100.
Il parcourt les 50 premiers kilomètres en 2h, puisque sa vitesse est alors de 25 km/h.
Les 50 km suivants sont parcourus à la vitesse de 15 km/h ; le parcours dure donc
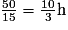 .
.La vitesse moyenne sur l'ensemble du parcours est donc :
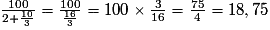 km/h.
km/h.L'affirmation 1 est fausse.
Remarque : l'affirmation proposée confronte la réflexion à une représentation erronée assez commune, selon laquelle la vitesse moyenne sur un parcours aller-retour, par exemple, est la moyenne de la vitesse à l'aller et de la vitesse au retour.
2. Remarque : cet exercice, comme souvent lorsqu'il s'agit de numération, demande à écrire un nombre sous sa forme canonique, puis à en déduire sa décomposition canonique.
Un nombre entier N à trois chiffres dont les chiffres des centaines, dizaines et unités sont les mêmes peut s'écrire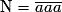 avec 0 < a
avec 0 < a  9. On en déduit :
9. On en déduit :
N = 100a + 10a + a = 111a = 37 × aa. N est donc multiple de 37.
L'affirmation 2 est vraie.
Un nombre entier N à trois chiffres dont les chiffres des centaines, dizaines et unités sont les mêmes peut s'écrire
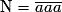 avec 0 < a
avec 0 < a  9. On en déduit :
9. On en déduit :N = 100a + 10a + a = 111a = 37 × aa. N est donc multiple de 37.
L'affirmation 2 est vraie.
3. Rappel : deux nombres sont dits premiers entre eux s'ils n'ont pas de diviseur commun.
7 et 21 sont tous deux impairs mais ne sont pas premiers entre eux, puisque 21 est multiple de 7.
L'affirmation 3 est fausse.
7 et 21 sont tous deux impairs mais ne sont pas premiers entre eux, puisque 21 est multiple de 7.
L'affirmation 3 est fausse.
4. Rappel : deux nombres sont dits inverses l'un de l'autre si leur produit est égal à 1.
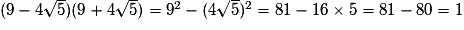
L'affirmation 4 est vraie.
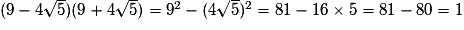
L'affirmation 4 est vraie.
5. Rappel : le périmètre d'un cercle de diamètre d est πd. Le demi-périmètre de ce même cercle est donc : πd/2.
Soit x la longueur AI et y la longueur IB. Le trait plein est constitué d'un demi-cercle de diamètre x suivi d'un demi-cercle de diamètre y.
La longueur de ce chemin est :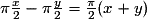 .
.
Le trait en pointillé est un demi-cercle de diamètre x + y. Sa longueur est :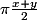 .
.
Les deux chemins ont la même longueur.
L'affirmation 5 est vraie.
Soit x la longueur AI et y la longueur IB. Le trait plein est constitué d'un demi-cercle de diamètre x suivi d'un demi-cercle de diamètre y.
La longueur de ce chemin est :
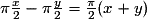 .
.Le trait en pointillé est un demi-cercle de diamètre x + y. Sa longueur est :
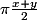 .
.Les deux chemins ont la même longueur.
L'affirmation 5 est vraie.
 |
6. Une augmentation de 20 % par heure correspond à une multiplication du nombre de bactéries par 1,2 toutes les heures. Au bout de 5 heures, le nombre initial de bactéries a donc été multiplié par (1,2)5 = 2,48832 et non pas 2.
L'affirmation 6 est donc fausse.
L'affirmation 6 est donc fausse.
Exercice 2
Partie 1
1. La fonction qui associe à la vitesse v d'un véhicule sa distance de freinage est : f(v) = 0,08v.
1. a) La formule à entrer dans la cellule B2 afin de compléter la ligne 2 par recopiage vers la droite est : « =0,08*B1*B1 » ou : « $B$3*B1*B1 ».
1. b) La première formule proposée ne permet pas le recalcul automatique des distances de freinage en ligne 2 en cas de modification du coefficient ; en revanche, la deuxième formule le permet, puisque ce n'est pas la valeur 0,08 qui est entrée pour le coefficient, mais la valeur prise par la cellule B3. Cette cellule n'est pas modifiée par le recopiage à droite, puisque le numéro de la ligne (resp. de la colonne) est précédé du signe $.
2. a) Une lecture attentive de l'énoncé doit permettre de s'assurer que les mesures de grandeurs sont exprimées dans des unités compatibles. Ici, la fonction f fournit la distance de freinage en mètres, en fonction d'une vitesse exprimée en mètres par secondes. C'est dans cette unité-quotient qu'il faut exprimer la vitesse considérée, avant de calculer la distance de freinage correspondante.
72 km/h = 72 000 m/h = 72 000 m/3 600 s = 20 m/s.
Si v = 20 m/s, alors f(v) = 0,08 × 202 = 32 m.
72 km/h = 72 000 m/h = 72 000 m/3 600 s = 20 m/s.
Si v = 20 m/s, alors f(v) = 0,08 × 202 = 32 m.
2. b) f(v) > 45 équivaut à : 0,08v2 > 45, soit : v2 > 562,5 d'où v > 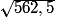 car v est positive.
car v est positive.
Or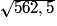 m/s =
m/s = 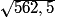 × 3 600 m/h =
× 3 600 m/h =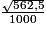 × 3 600 km/h
× 3 600 km/h 85 km/h.
85 km/h.
La distance de freinage sur route sèche est supérieure à 45 mètres pour une vitesse supérieure à 85 km/h.
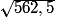 car v est positive.
car v est positive.Or
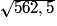 m/s =
m/s = 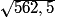 × 3 600 m/h =
× 3 600 m/h =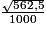 × 3 600 km/h
× 3 600 km/h 85 km/h.
85 km/h.La distance de freinage sur route sèche est supérieure à 45 mètres pour une vitesse supérieure à 85 km/h.
Partie 2
1. Soit k le coefficient cherché.
Sur le graphique, on lit que f(30) = 144, c'est-à-dire que k302 = 144.
On en déduit que k =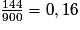 .
.
Sur le graphique, on lit que f(30) = 144, c'est-à-dire que k302 = 144.
On en déduit que k =
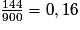 .
.2. Comme 0,08 < 0,16 la représentation graphique de la distance de freinage sur route sèche en fonction de la vitesse serait une courbe située en-dessous de celle proposée : à vitesse constante, la distance de freinage est moindre sur route sèche que sur route mouillée. Une justification calculatoire étant demandée, on peut proposer le tableau suivant, dans lequel les valeurs de la première et de la deuxième ligne sont prélevées sur le graphique, et celles de la troisième ligne sont obtenues par le calcul en utilisant la formule de la première partie :
| vitesse en m/s | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
| distance de freinage sur route mouillée (en m) | 0 | 5 | 16 | 36 | 64 | 100 | 144 |
| distance de freinage sur route sèche (en m) | 0 | 2 | 8 | 18 | 32 | 50 | 72 |
Problème
Partie A
Remarque : l'énoncé fournit une définition d'un polygone régulier qui n'est peut-être pas celle que vous connaissez : il faut se baser sur cette définition et en déduire les propriétés à mobiliser pour l'exercice…
 |
L'hexagone régulier ABCDEF est inscrit dans un cercle de centre O et de rayon r, on en déduit que : OA = OB = OC = OD = OE = OF = r (1) et que :
AB = BC = CD = DE = EF = FA (2).
On déduit des égalités (1) et (2) que les triangles AOB, BOC, COD, DOE, EOF, FOA sont isométriques (superposables). Ces triangles, qui sont par hypothèse isocèles, sont en fait équilatéraux, puisque :
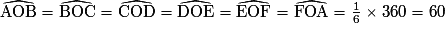 °
°
Calculons à présent l'aire de l'hexagone.
On a, d'après ce qui précède : AABCDEF = 6AAOB. Or AAOB =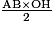 .
.
Le triangle AOB étant équilatéral, la hauteur (OH) est également la médiatrice du côté [AB], donc H est le milieu de [AB]. D'après le théorème de Pythagore dans le triangle AHO, rectangle en H, on a : AH2 + HO2 = AO2 d'où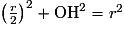 et donc :
et donc : 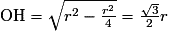 .
.
On en déduit :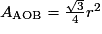 et :
et :
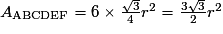 .
.
AB = BC = CD = DE = EF = FA (2).
On déduit des égalités (1) et (2) que les triangles AOB, BOC, COD, DOE, EOF, FOA sont isométriques (superposables). Ces triangles, qui sont par hypothèse isocèles, sont en fait équilatéraux, puisque :
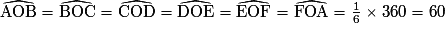 °
°Calculons à présent l'aire de l'hexagone.
On a, d'après ce qui précède : AABCDEF = 6AAOB. Or AAOB =
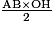 .
.Le triangle AOB étant équilatéral, la hauteur (OH) est également la médiatrice du côté [AB], donc H est le milieu de [AB]. D'après le théorème de Pythagore dans le triangle AHO, rectangle en H, on a : AH2 + HO2 = AO2 d'où
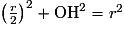 et donc :
et donc : 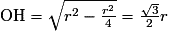 .
.On en déduit :
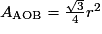 et :
et :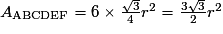 .
.Partie B
1. L'écrou a la forme d'un prisme droit de hauteur 8 mm et de base un hexagone régulier de rayon 9,45 mm, auquel on a retiré un cylindre de hauteur 8 mm et dont la base a un rayon de 5 mm. Les formules de volume du prisme droit et du cylindre sont les suivantes :
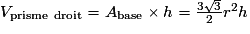 d'après la partie A, r étant le rayon du cercle circonscrit à la base hexagonale du prisme et h sa hauteur ;
d'après la partie A, r étant le rayon du cercle circonscrit à la base hexagonale du prisme et h sa hauteur ;
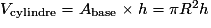 où h est la hauteur du cylindre et R le rayon de sa base.
où h est la hauteur du cylindre et R le rayon de sa base.
On a donc :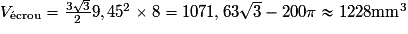
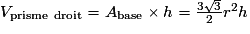 d'après la partie A, r étant le rayon du cercle circonscrit à la base hexagonale du prisme et h sa hauteur ;
d'après la partie A, r étant le rayon du cercle circonscrit à la base hexagonale du prisme et h sa hauteur ;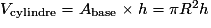 où h est la hauteur du cylindre et R le rayon de sa base.
où h est la hauteur du cylindre et R le rayon de sa base.On a donc :
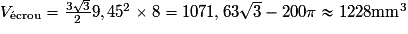
2. La masse volumique du laiton est de 8 400 kg/m3, ce qui correspond à 8 400 000 g/m3, soit 0,0084 g/mm3. On obtient la masse de l'écrou en multipliant son volume par la masse volumique ; la masse de l'écrou est donc d'environ 10 g.
Partie C
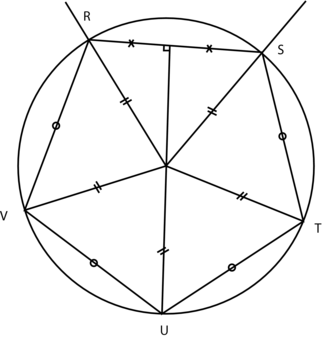 |
1. Les triangles ROS, SOT, TOU, UOV et VOR sont isométriques car RS = ST = TU = UV = VR et OR = OS = OT = OU = OV. Ces triangles sont également isocèles, mais pas équilatéraux, contrairement à la situation de la partie A, car  °.
°.
Le triangle ROS étant isocèle en O, la hauteur (OH) est également la bissectrice de l'angle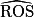 donc
donc 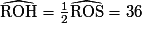 °.
°.
Dans le triangle ROH, rectangle en H, on a :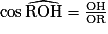 ;
;
d'où OH = r × cos36° car OR = r et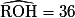 °.
°.
 °.
°.Le triangle ROS étant isocèle en O, la hauteur (OH) est également la bissectrice de l'angle
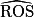 donc
donc 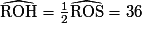 °.
°.Dans le triangle ROH, rectangle en H, on a :
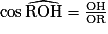 ;
;d'où OH = r × cos36° car OR = r et
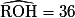 °.
°.2. L'aire du pentagone RSTUV est égale à cinq fois l'aire du triangle ROS.
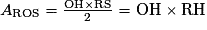 car H est le milieu du côté [RS], le triangle ROS étant isocèle en O.
car H est le milieu du côté [RS], le triangle ROS étant isocèle en O.
Calculons RH. Dans le triangle ROH, rectangle en H, on a :
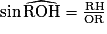 d'où RH = r × sin36°.
d'où RH = r × sin36°.
On en déduit que : AROS = r × cos36° × r × sin36° = r2cos36°sin36°.
Finalement, ARSTUV = 5cos36°sin36°r2.
Remarque : cette dernière formule est « simplifiable » en :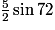 °r2, mais les formules permettant le passage à cette écriture sont hors programme du CRPE.
°r2, mais les formules permettant le passage à cette écriture sont hors programme du CRPE.
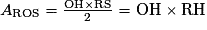 car H est le milieu du côté [RS], le triangle ROS étant isocèle en O.
car H est le milieu du côté [RS], le triangle ROS étant isocèle en O.Calculons RH. Dans le triangle ROH, rectangle en H, on a :
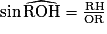 d'où RH = r × sin36°.
d'où RH = r × sin36°.On en déduit que : AROS = r × cos36° × r × sin36° = r2cos36°sin36°.
Finalement, ARSTUV = 5cos36°sin36°r2.
Remarque : cette dernière formule est « simplifiable » en :
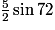 °r2, mais les formules permettant le passage à cette écriture sont hors programme du CRPE.
°r2, mais les formules permettant le passage à cette écriture sont hors programme du CRPE.