Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
Toutes les réponses seront justifiées.
1) Donner les restes des divisions par 6 et par 3 de chacune des trois sommes suivantes :
5 + 7 + 9
15 + 17 + 19
1 527 + 1 529 + 1 531
5 + 7 + 9
15 + 17 + 19
1 527 + 1 529 + 1 531
2)
Plus généralement :
a. Donner le reste de la division par 6 de la somme de trois nombres impairs consécutifs.
b. Donner le reste de la division par 3 de la somme de trois nombres impairs consécutifs.
3) Trouver trois nombres impairs consécutifs dont la somme est 12 027.
4) On cherche un nombre p tel que la somme de p nombres entiers impairs consécutifs soit toujours un multiple de 5. Déterminer la plus petite valeur possible de p.
Question complémentaire (4 points)
Cet exercice s'appuie sur les documents proposés dans les annexes 1 et 2 :
- Annexe 1 : une situation inspirée d'une activité – Partages inéquitables – proposée dans l'ouvrage ERMEL Apprentissages numériques et résolution de problèmes, CP, Éd. Hatier.
- Annexe 2 : les travaux d'un élève (Hubert).
1) Citer deux objectifs que peut viser un enseignant qui propose cette activité à ses élèves. Justifier.
2) Indiquer deux éléments de cette situation qui peuvent avoir une influence sur les procédures mises en œuvre par les élèves.
3) Quel est le rôle de la première phase ?
4) Décrire deux procédures différentes que peuvent utiliser les élèves pour réussir la tâche demandée au cours de la deuxième phase.
5) Analyser la procédure élaborée par Hubert.
Exercice 2 (4 points)
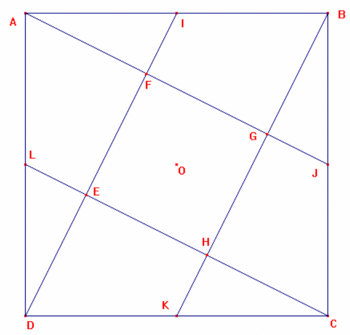 |
ABCD est un carré de centre O, et I, J, K et L sont les milieux de chacun de ses côtés. Le segment [AJ] coupe les segments [DI] et [BK] en F et G respectivement ; le segment [CL] coupe les segments [BK] et [DI] en H et E respectivement.
On désigne par a la longueur des côtés du carré ABCD.
On désigne par a la longueur des côtés du carré ABCD.
1) Démontrer que le quadrilatère BKDI est un parallélogramme. Calculer en fonction de a la longueur de ses côtés.
2)
On admet que le quadrilatère EFGH est un carré (on ne demande pas de le démontrer).
a. Montrer que : 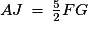 .
.
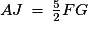 .
.b. En déduire le rapport 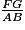 , puis le rapport des aires des deux carrés.
, puis le rapport des aires des deux carrés.
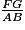 , puis le rapport des aires des deux carrés.
, puis le rapport des aires des deux carrés.3)
a. On appelle M le milieu du segment [FG]. Démontrer que les trois points E, M et B sont alignés.
b. On veut construire un carré PQRS à l'intérieur du carré EFGH, par le même procédé qui a permis de construire le carré EFGH à l'intérieur du carré ABCD.
Expliquer pourquoi cette construction peut être réalisée à l'aide uniquement d'une règle non graduée (sans compas ni équerre).
Expliquer pourquoi cette construction peut être réalisée à l'aide uniquement d'une règle non graduée (sans compas ni équerre).
c. Calculer en fonction de a la longueur du côté du carré PQRS.
Exercice 3 (4 points)
On s'intéresse à la fabrication d'emballages ayant la forme d'un parallélépipède rectangle, appelés « bricks ».
On néglige l'épaisseur de la matière utilisée pour ces emballages.
On néglige l'épaisseur de la matière utilisée pour ces emballages.
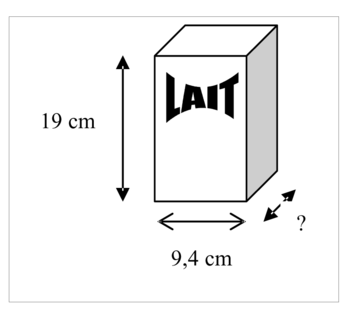 |
1) Une des faces rectangulaires d'un brick de 1 litre de lait a pour dimensions 19 cm et 9,4 cm.
Calculer la troisième dimension du brick et en donner une valeur approchée par excès au millimètre près.
Calculer la troisième dimension du brick et en donner une valeur approchée par excès au millimètre près.
2)
a. La hauteur d'un brick à base carrée de 1 litre de jus d'orange mesure 20 cm.
Calculer la longueur du côté du carré. En donner une valeur approchée par excès au millimètre près.
Calculer la longueur du côté du carré. En donner une valeur approchée par excès au millimètre près.
b. On souhaite modifier la hauteur du brick précédent pour que, en conservant la même base, il contienne 20 % de jus d'orange en plus.
Déterminer la nouvelle hauteur.
Déterminer la nouvelle hauteur.
3) On considère les bricks de volume 1 dm3 dont les mesures en centimètre des arêtes sont des entiers supérieurs à 3.
Déterminer toutes les possibilités. Justifier.
Déterminer toutes les possibilités. Justifier.
4) Dessiner deux patrons différents d'un même parallélépipède rectangle, dont les trois dimensions sont distinctes, en indiquant clairement par un codage les côtés de même longueur.
Question complémentaire (4 points)
Un enseignant de CM2 analyse les documents pédagogiques reproduits dans les annexes 3 et 4.1) Dans l'annexe 3, préciser en quoi la situation proposée contribue à l'élaboration du langage géométrique à connaître à ce niveau.
2)
Dans l'annexe 4, l'activité demande à l'élève de chercher d'autres patrons du cube.
a. En utilisant l'annexe 5, indiquer les compétences visées par cette activité. Expliciter votre réponse.
b. Pour faire cette activité, il est suggéré aux élèves de manipuler « six faces cartonnées ».
L'annexe 5 précise que « le recours à des matériels variés permet d'insister sur des aspects différents d'un solide ». Indiquer l'intérêt pédagogique d'une construction d'un cube à partir de « tiges ».
L'annexe 5 précise que « le recours à des matériels variés permet d'insister sur des aspects différents d'un solide ». Indiquer l'intérêt pédagogique d'une construction d'un cube à partir de « tiges ».
Annexe 1
Les partages inéquitables
Première phase : résolution d'un problème avec du matériel
Les enfants sont répartis en groupes.Matériel
- Pour chaque groupe, on donne un couvercle de boîte à chaussures contenant des objets (bâtonnets de glace) : 16, 19 et 27 selon les groupes.
- Des boîtes (pots de yaourt) : 4, 5 ou 7.
« Il va falloir mettre les objets dans les boîtes. Il doit y avoir 3, 4 ou 5 objets par boîte. Pas moins de 3, pas plus de 5. Tous les objets doivent être utilisés. »
Les élèves travaillent en groupes avec pour tâche de remplir les boîtes. Chaque groupe est ensuite amené à présenter son résultat, c'est-à-dire ce qu'il a obtenu et comment il l'a obtenu. On vérifie ensuite l'exactitude de chaque répartition.
Deuxième phase : résolution du problème sans matériel
On applique toujours la consigne précédente.
Dans cette étape, les objets ainsi que les boîtes ne sont plus présents. Chaque enfant dispose d'une feuille de recherche. Le maître y indique dans les cadres réservés, le nombre de boîtes et le nombre de bâtonnets.
Les répartitions suivantes sont proposées :
Dans cette étape, les objets ainsi que les boîtes ne sont plus présents. Chaque enfant dispose d'une feuille de recherche. Le maître y indique dans les cadres réservés, le nombre de boîtes et le nombre de bâtonnets.
Les répartitions suivantes sont proposées :
- 13 bâtonnets à répartir dans 4 boîtes ;
- 18 bâtonnets à répartir dans 4 boîtes ;
- 23 bâtonnets à répartir dans 6 boîtes ;
- 26 bâtonnets à répartir dans 6 boîtes ;
- 31 bâtonnets à répartir dans 7 boîtes.
 |
Cette phase de recherche est suivie d'une mise en commun.
Annexe 2
 |
Annexe 3
Travaux géométriques au cycle 3
Situation 3 : le solide à retrouver
Présentation de la situationC'est un jeu de portrait. Les élèves posent des questions afin d'obtenir des renseignements qui doivent leur permettre de trouver un solide choisi parmi une collection de solides réels.
Compétence visée
Décrire un polyèdre.
Objectifs
Placer les élèves dans une situation où ils doivent :
- élaborer des questions relatives aux propriétés géométriques d'objets à trois dimensions et interpréter les réponses fournies pour retrouver un polyèdre choisi à l'avance ;
- élaborer un langage adapté au domaine des polyèdres.
Matériel :
Un lot de solides.
Situation :
Les élèves sont répartis par groupes de quatre. L'enseignant a choisi un solide.
Il communique son choix à un groupe, le groupe R. Les autres groupes vont poser des questions à tour de rôle au groupe R afin de retrouver le solide choisi. Les questions ne peuvent porter que sur les formes des objets ou sur les éléments géométriques qui constituent ceux-ci (elles ne peuvent être relatives ni à une couleur, ni à la place qu'occupe l'objet choisi dans le lot).
Les réponses du groupe R sont fermées, elles ne peuvent être que « oui », « non » ou « on ne peut pas répondre ».
 |
D'après « Travaux géométriques au cycle 3 » (CRDP du Nord-Pas-de-Calais).
Annexe 4
Cherche d'autres patrons du cube.
Découpe le patron en suivant les traits pleins et plie-le selon les traits pointillés.
Pour trouver d'autres patrons du cube, tu peux manipuler 6 faces cartonnées et faire des essais ; puis les dessiner au fur et à mesure.
Découpe le patron en suivant les traits pleins et plie-le selon les traits pointillés.
Pour trouver d'autres patrons du cube, tu peux manipuler 6 faces cartonnées et faire des essais ; puis les dessiner au fur et à mesure.
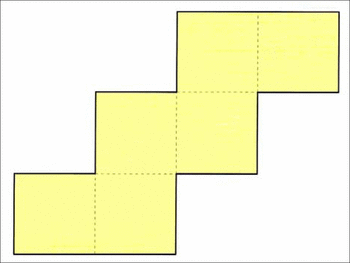 |
D'après « Math + », Éd. Sed, CM2.
Annexe 5
Solides : cube, parallélépipède rectangle
| Compétences | Commentaires |
|---|---|
| Percevoir un solide, en donner le nom. Vérifier certaines propriétés relatives aux faces ou arêtes d'un solide à l'aide des instruments. | Les compétences sont relatives à une liste limitée de solides, mais les activités qui permettent de construire ces compétences peuvent concerner d'autres solides (prisme, pyramide, sphère, cylindre, cône). L'identification se fait parmi d'autres solides ou parmi des représentations planes de solides (vues, patrons). |
| Décrire un solide en vue de l'identifier dans un lot de solides ou de le faire reproduire sans équivoque. | Le travail sur la perspective cavalière relève du collège : seules des activités relatives à la lecture de telles représentations sont envisagées au cycle 3 (reconnaissance de certains solides ou mise en correspondance du solide réel avec une représentation en perspective). |
| Construire un solide. | La construction est réalisée à partir d'éléments simples (faces rectangulaires ou triangulaires), en assemblant des solides simples ou en utilisant des patrons. Le recours à des matériels variés permet d'insister sur des aspects différents d'un solide (carton pour les faces, tiges pour les arêtes) et d'envisager, par exemple, la reproduction d'un solide construit à partir de ses arêtes (tiges) à l'aide de ses faces (carton). |
| Reconnaître, construire ou compléter un patron de cube, de parallélépipède rectangle. Utiliser à bon escient le vocabulaire suivant : cube, parallélépipède rectangle ; sommet, arête, face. | Pour les solides, les activités où s'établissent des relations entre espace et plan sont privilégiées. Par exemple, la description d'un solide conduit à prendre des empreintes des faces, à s'interroger sur la nature de ces faces ; la nécessité d'en construire un autre identique amène à l'élaboration d'un patron du solide, puis à son remontage. D'autres solides que le cube ou le parallélépipède rectangle peuvent donner lieu à la réalisation de patrons. |
Extrait des documents d'application des programmes pour le cycle 3.
Corrigé
Corrigé
Exercice 1 (4 points)
1)
5 + 7 + 9 = 21
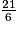 = 3 reste 3
= 3 reste 3
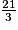 = 7 reste 0
= 7 reste 0
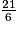 = 3 reste 3
= 3 reste 3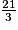 = 7 reste 0
= 7 reste 015 + 17 + 19 = 51
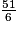 = 8 reste 3
= 8 reste 3
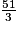 = 17 reste 0
= 17 reste 0
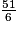 = 8 reste 3
= 8 reste 3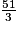 = 17 reste 0
= 17 reste 01 527 + 1 529 + 1 531 = 4 587
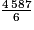 = 764 reste 3
= 764 reste 3
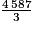 = 1 529 reste 0
= 1 529 reste 0
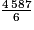 = 764 reste 3
= 764 reste 3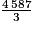 = 1 529 reste 0
= 1 529 reste 02)
a. Soient trois nombres entiers impairs consécutifs x, x + 2 et x + 4.
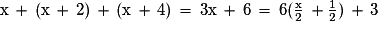 .
.
Donc cette somme n'est pas un multiple de 6 et le reste de la division de cette somme par 6 est 3.
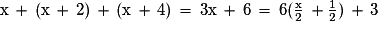 .
.Donc cette somme n'est pas un multiple de 6 et le reste de la division de cette somme par 6 est 3.
b. Soient trois nombres entiers impairs consécutifs x, x + 2 et x + 4.
x + (x + 2) + (x + 4) = 3x + 6 = 3(x + 2).
Cette somme est un multiple de 3, donc le reste de la division de cette somme par 3 est nul.
x + (x + 2) + (x + 4) = 3x + 6 = 3(x + 2).
Cette somme est un multiple de 3, donc le reste de la division de cette somme par 3 est nul.
3) Soient trois nombres entiers impairs consécutifs x, x + 2 et x + 4.
On résout l'équation : x + (x + 2) + (x + 4) = 12 027.
3x + 6 = 12 027
3x = 12 021
x = 4 007.
Donc les trois nombres entiers impairs consécutifs sont 4 007, 4 009 et 4 011.
On résout l'équation : x + (x + 2) + (x + 4) = 12 027.
3x + 6 = 12 027
3x = 12 021
x = 4 007.
Donc les trois nombres entiers impairs consécutifs sont 4 007, 4 009 et 4 011.
4) Soient les nombres entiers impairs consécutifs x, x + 2, x + 4, …
Pour que leur somme soit un multiple de 5, il est nécessaire que le nombre de termes en « x » soit un multiple de 5, donc il faut au minimum compter 5x.
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) = 5x + 10 = 5(x + 2) et 5(x + 2) est un multiple de 5.
Donc la somme de 5 nombres entiers impairs consécutifs est un multiple de 5.
Soit p = 5.
Pour que leur somme soit un multiple de 5, il est nécessaire que le nombre de termes en « x » soit un multiple de 5, donc il faut au minimum compter 5x.
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) = 5x + 10 = 5(x + 2) et 5(x + 2) est un multiple de 5.
Donc la somme de 5 nombres entiers impairs consécutifs est un multiple de 5.
Soit p = 5.
Question complémentaire (4 points)
1) Un des objectifs de l'enseignant est de mettre les élèves devant une situation de partage à réaliser avec des contraintes de quantité (nombre total de bâtonnets et de boîtes) et de répartition (« pas moins de », « pas plus de »).
Il peut aussi travailler sur le vocabulaire et la compréhension de « pas moins de » et « pas plus de », formulations qui posent souvent des problèmes aux élèves.
Il peut aussi travailler sur le vocabulaire et la compréhension de « pas moins de » et « pas plus de », formulations qui posent souvent des problèmes aux élèves.
2) Le fait de faire travailler les élèves en groupes sur une situation de partage va les amener à reproduire une activité vécue en cours de récréation, non pas avec des billes ou des bonbons, mais avec des bâtonnets. Chacun dans le groupe peut prendre une boîte et un des élèves peut faire la distribution des bâtonnets.
Par ailleurs, le fait d'avoir choisi des nombres très proches, « pas moins de 3 » et « pas plus de 5 », forcera les élèves à faire très attention à cette distribution.
Par ailleurs, le fait d'avoir choisi des nombres très proches, « pas moins de 3 » et « pas plus de 5 », forcera les élèves à faire très attention à cette distribution.
3) La première phase de l'activité se déroule en groupes et avec du matériel concret. Elle vise à motiver les élèves et à les aider à tous rentrer dans l'activité. Comme il est difficile d'intégrer toutes les consignes de l'exercice, l'enseignant mise sur le fait que le groupe facilitera la résolution du problème : si un élève a oublié ou mal lu une contrainte, un autre membre du groupe pourra s'en rendre compte.
4) Il est difficile d'intégrer toutes les contraintes en même temps. Les élèves vont choisir de partir :
- soit de la contrainte « pas moins de trois bâtonnets dans chaque boîte », en mettant au départ trois bâtonnets dans chaque boîte, puis en complétant pour avoir le nombre total de bâtonnets demandé sans dépasser cinq bâtonnets par boîte ;
- soit de la contrainte « pas plus de cinq bâtonnets par boîte », en mettant le maximum de cinq bâtonnets dans les premières boîtes, puis en en retirant si les dernières boîtes ne contiennent pas assez de bâtonnets pour répondre à la consigne « plus de trois ».
5) Hubert doit mettre 31 bâtonnets dans 7 boîtes, et d'après la consigne, il doit y avoir 3, 4 ou 5 bâtonnets par boîte. Il choisit de mettre dans chacune des six premières boîtes le maximum de bâtonnets, soit 5 ; puis dans la dernière boîte, il met 1 bâtonnet pour arriver au total de 31. C'est sa première addition. Ensuite, il réajuste, enlève des bâtonnets dans 3 boîtes pour obtenir 31 sans dépasser 5 bâtonnets par boîte.
Exercice 2 (4 points)
1) IB = DK = 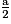 .
.
De plus, AID et BKC sont deux triangles rectangles isométriques, donc DI = BK = longueur de l'hypoténuse du triangle AID. Or « un quadrilatère, non croisé, qui a ses côtés opposés de même longueur est un parallélogramme ». Donc BKDI est un parallélogramme.
Longueur des côtés de BKDI :
IB = DK =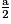 .
.
Calcul de ID :
On applique le théorème de Pythagore dans le triangle AID, rectangle en A :
ID2 = AI2 + AD2
ID2 =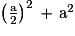
ID2 =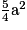
donc ID =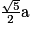 .
.
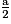 .
.De plus, AID et BKC sont deux triangles rectangles isométriques, donc DI = BK = longueur de l'hypoténuse du triangle AID. Or « un quadrilatère, non croisé, qui a ses côtés opposés de même longueur est un parallélogramme ». Donc BKDI est un parallélogramme.
Longueur des côtés de BKDI :
IB = DK =
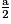 .
.Calcul de ID :
On applique le théorème de Pythagore dans le triangle AID, rectangle en A :
ID2 = AI2 + AD2
ID2 =
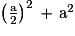
ID2 =
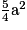
donc ID =
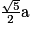 .
.2)
a. On applique le théorème de Thalés dans le triangle ABG avec (IF) // (GB) car BKDI est un parallélogramme. On a 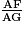 =
= 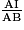 =
= 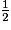 , donc AF =
, donc AF = 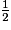 AG, et A, F, G sont alignés, donc AF = FG.
AG, et A, F, G sont alignés, donc AF = FG.
Par ailleurs, dans le triangle BCK, on applique le théorème de Thalés avec (GJ) // (HC) car FGHE étant un carré, (AJ) // (LC) : on a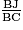 =
= 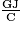 =
= 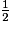 .
.
Donc GJ =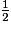 HC =
HC = 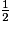 FG.
FG.
Finalement, AJ = 2 × FG +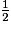 FG, soit AJ =
FG, soit AJ = 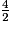 FG +
FG + 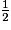 FG =
FG = 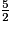 FG.
FG.
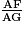 =
= 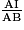 =
= 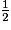 , donc AF =
, donc AF = 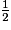 AG, et A, F, G sont alignés, donc AF = FG.
AG, et A, F, G sont alignés, donc AF = FG.Par ailleurs, dans le triangle BCK, on applique le théorème de Thalés avec (GJ) // (HC) car FGHE étant un carré, (AJ) // (LC) : on a
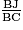 =
= 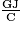 =
= 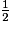 .
.Donc GJ =
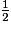 HC =
HC = 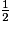 FG.
FG.Finalement, AJ = 2 × FG +
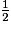 FG, soit AJ =
FG, soit AJ = 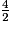 FG +
FG + 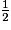 FG =
FG = 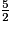 FG.
FG.b. 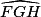 est un angle droit car EFGH est un carré. Donc
est un angle droit car EFGH est un carré. Donc 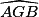 est aussi un angle droit. On applique le théorème de Pythagore dans le triangle AGB rectangle en G.
est aussi un angle droit. On applique le théorème de Pythagore dans le triangle AGB rectangle en G.
On a AG2 + GB2 = AB2.
Or AF = FG = GB.
Donc (2FG)2 + FG2 = AB2
5 FG2 = AB2
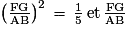 > 0.
> 0.
Donc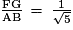
et .
.
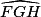 est un angle droit car EFGH est un carré. Donc
est un angle droit car EFGH est un carré. Donc 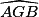 est aussi un angle droit. On applique le théorème de Pythagore dans le triangle AGB rectangle en G.
est aussi un angle droit. On applique le théorème de Pythagore dans le triangle AGB rectangle en G.On a AG2 + GB2 = AB2.
Or AF = FG = GB.
Donc (2FG)2 + FG2 = AB2
5 FG2 = AB2
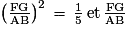 > 0.
> 0.Donc
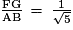
et
 .
.3)
a. Dans le triangle EBH, G est le milieu de [BH] et (GM) // (EH), car M  [FG] et (FG) // (EH), EFGH étant un carré. Donc M est le milieu de [EB]. Donc E, M et B sont des points alignés.
[FG] et (FG) // (EH), EFGH étant un carré. Donc M est le milieu de [EB]. Donc E, M et B sont des points alignés.
 [FG] et (FG) // (EH), EFGH étant un carré. Donc M est le milieu de [EB]. Donc E, M et B sont des points alignés.
[FG] et (FG) // (EH), EFGH étant un carré. Donc M est le milieu de [EB]. Donc E, M et B sont des points alignés.b. On n'a pas besoin de placer le milieu de [FG] (et donc de prendre une règle graduée) car on sait d'après 3)a. qu'il sera aligné avec les points E et B. Il suffit de tracer (EB).
De la même façon, il suffit de tracer les droites (FC), (HA) et (DG) et on obtient le carré PQRS sans utiliser ni équerre ni règle graduée, une règle non graduée suffit.
De la même façon, il suffit de tracer les droites (FC), (HA) et (DG) et on obtient le carré PQRS sans utiliser ni équerre ni règle graduée, une règle non graduée suffit.
c. On construit un carré PQRS à l'intérieur du carré EFGH par le même procédé de construction que pour le carré EFGH dans le carré ABCD, donc par analogie :
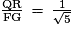 , soit
, soit 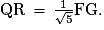
Or d'après 2)b.,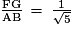 , avec AB = a, donc FG =
, avec AB = a, donc FG = 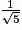 a.
a.
Donc QR =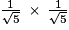 a.
a.
Soit QR =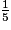 a.
a.
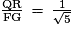 , soit
, soit 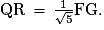
Or d'après 2)b.,
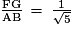 , avec AB = a, donc FG =
, avec AB = a, donc FG = 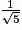 a.
a.Donc QR =
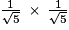 a.
a.Soit QR =
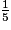 a.
a.Exercice 3 (4 points)
1) 1 L = 1 dm3 = 1 000 cm3.
Volume du pavé droit = profondeur × largeur × hauteur.
1 000 = profondeur × 9,4 × 19.
Donc profondeur =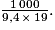
Soit profondeur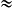 5,6 cm (valeur par excès au millimètre près).
5,6 cm (valeur par excès au millimètre près).
Volume du pavé droit = profondeur × largeur × hauteur.
1 000 = profondeur × 9,4 × 19.
Donc profondeur =
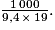
Soit profondeur
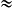 5,6 cm (valeur par excès au millimètre près).
5,6 cm (valeur par excès au millimètre près).2)
a. Volume = côté × côté × hauteur
1 000 = côté2 × 20.
Donc côté2 = 50.
Soit côté =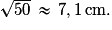 (valeur par excès au millimètre près).
(valeur par excès au millimètre près).
1 000 = côté2 × 20.
Donc côté2 = 50.
Soit côté =
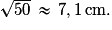 (valeur par excès au millimètre près).
(valeur par excès au millimètre près).b. Nouveau volume = (1 + 20 %) × 1 000 = 1 200 cm3.
Nouvelle hauteur =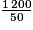 = 24 cm.
= 24 cm.
En conservant la même base, un brick qui contient 20 % de jus d'orange en plus a une hauteur de 24 cm.
Nouvelle hauteur =
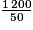 = 24 cm.
= 24 cm.En conservant la même base, un brick qui contient 20 % de jus d'orange en plus a une hauteur de 24 cm.
3) Volume = 1 dm3 = 1 000 cm3.
1 000 est un multiple de 2, 4, 5, 10, 20, 25, 40, 50, 100, 250, 500.
Les mesures des arêtes cherchées sont des entiers supérieurs à 3, donc les seules possibilités sont les suivantes :
1 000 = 4 × 25 × 10
1 000 = 10 × 10 × 10
1 000 = 4 × 5 × 50
1 000 = 5 × 20 × 10
1 000 = 5 × 40 × 5.
1 000 est un multiple de 2, 4, 5, 10, 20, 25, 40, 50, 100, 250, 500.
Les mesures des arêtes cherchées sont des entiers supérieurs à 3, donc les seules possibilités sont les suivantes :
1 000 = 4 × 25 × 10
1 000 = 10 × 10 × 10
1 000 = 4 × 5 × 50
1 000 = 5 × 20 × 10
1 000 = 5 × 40 × 5.
4)
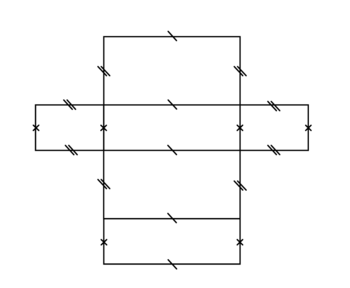 |
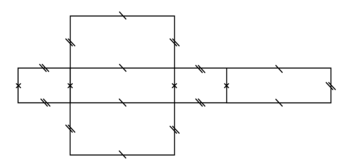 |
Question complémentaire (4 points)
1) La situation proposée a pour but de travailler sur les noms des divers solides. Ce jeu de portrait oblige les élèves à utiliser le vocabulaire varié et précis de la géométrie pour se faire comprendre de leurs camarades. Ils vont devoir utiliser les mots « arêtes », « faces », « sommets » de la géométrie dans l'espace, mais aussi réinvestir le vocabulaire de la géométrie plane nécessaire à la description des faces de ces solides.
2)
a. Les compétences visées sont :
- la perception d'un solide, ici un cube. En effet, le document propose le patron d'un cube, avec les pointillés apparents. Il est demandé de le découper et de le plier. Il s'agit ainsi d'aider l'élève à se représenter un cube et à en avoir une meilleure image mentale ;
- la construction d'un patron, et plus précisément d'un 2e patron de ce même cube avec 6 faces cartonnées. Le but est ici de réfléchir sur les propriétés et la nature de ces faces, mais aussi d'assimiler qu'il n'existe pas qu'un seul patron pour un cube donné.
b. L'intérêt pédagogique de la construction d'un cube à partir de « tiges » au lieu de carton est de travailler sur les arêtes au lieu des faces :
- qu'est-ce qu'une arête (Les élèves utilisent souvent à la place le mot « côté », réservé à la géométrie plane) ;
- quelles sont les propriétés des arêtes d'un cube.
