Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (3 points)
On justifiera toutes les réponses.
1) Peut-on trouver trois nombres entiers naturels consécutifs dont la somme est 207 ?
Si oui, lesquels ?
Si oui, lesquels ?
2) Peut-on trouver trois nombres entiers naturels consécutifs dont la somme est 329 ?
Si oui, lesquels ?
Si oui, lesquels ?
3) Caractériser les entiers naturels qui sont la somme de trois entiers consécutifs.
4) Déterminer toutes les valeurs possibles de d (avec 0  d
d  9) pour que le nombre dont l'écriture est
9) pour que le nombre dont l'écriture est 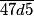 , en base 10, soit la somme de trois entiers naturels consécutifs.
, en base 10, soit la somme de trois entiers naturels consécutifs.
 d
d  9) pour que le nombre dont l'écriture est
9) pour que le nombre dont l'écriture est 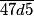 , en base 10, soit la somme de trois entiers naturels consécutifs.
, en base 10, soit la somme de trois entiers naturels consécutifs.Question complémentaire (5 points)
1) Un enseignant a demandé à ses élèves de cycle 3 d'écrire trois nombres entiers qui se suivent. Tous les élèves ont su répondre à cette question. L'enseignant leur a ensuite posé l'exercice suivant :
Je pense à trois nombres entiers qui se suivent. Lorsque je les additionne, je trouve 51. Quels sont ces nombres ?
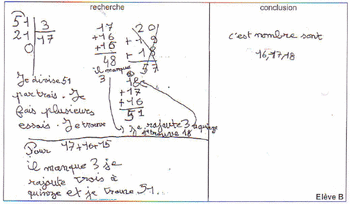
L'annexe comporte trois productions d'élèves. Décrire les procédures utilisées par les élèves, repérer et analyser les erreurs.
Je pense à trois nombres entiers qui se suivent. Lorsque je les additionne, je trouve 51. Quels sont ces nombres ?
L'annexe comporte trois productions d'élèves. Décrire les procédures utilisées par les élèves, repérer et analyser les erreurs.
2) Après une phase collective de mise en commun des productions d'élèves, l'enseignant répète la même consigne avec les nombres 72, 54 et 91, et en autorisant la calculatrice. Citer deux objectifs qui peuvent être visés par le professeur.
3)
L'enseignant demande ensuite aux élèves de chercher, avec l'aide de la calculatrice, pour chacun des nombres 51, 72, 54, 91, si on peut l'écrire comme le produit d'un nombre entier par 3.
a. Quel est l'objectif de cette dernière activité ?
b. Justifier l'emploi de la calculatrice.
Exercice 2 (2 points)
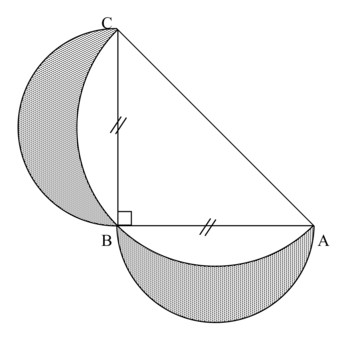
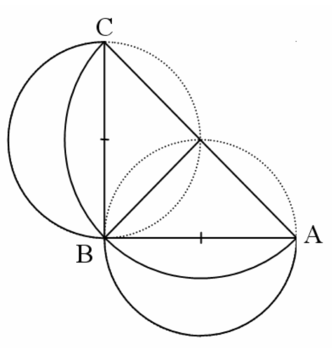
La figure ci-dessous est composée :
- d'un triangle isocèle ABC, rectangle en B,
- de trois demi-cercles ayant ses côtés pour diamètres.
1) À l'aide de la règle et du compas, reproduire cette figure (laisser apparents les traits de construction).
2) Sachant que AC = 7 cm, calculer l'aire totale des surfaces grisées (au mm2 près).
 |
Exercice 3 (4 points)
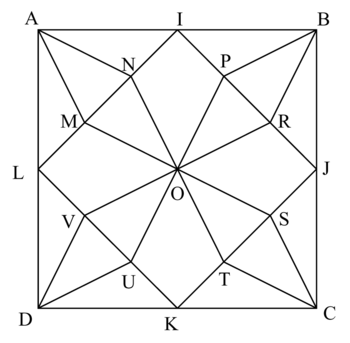
On donne les informations suivantes à propos de la figure ci-dessous :
- ABCD est un carré de 6 cm de côté ;
- les points I, J, K, L sont les milieux respectifs des côtés [AB], [BC], [CD], [DA] ;
- les points M et N appartiennent au segment [IL] et sont tels que les longueurs LM, MN, NI sont égales ;
- les points P, R, S, T, U, V sont placés de manière analogue sur les segments [IJ], [JK], [KL] ;
- le point O est le centre du carré ABCD.
 |
1)
Sans justifier les réponses :
a. citer les axes de symétrie de cette figure,
b. nommer l'image du triangle DUK par la symétrie de centre O.
2)
En justifiant les réponses :
a. déterminer la nature du triangle AIL,
b. calculer la longueur LM. Vérifier qu'on peut écrire le résultat sous la forme 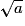 cm, où a est un nombre entier,
cm, où a est un nombre entier,
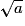 cm, où a est un nombre entier,
cm, où a est un nombre entier,c. déterminer la nature du quadrilatère IJKL.
3) On envisage de tracer la figure sur un quadrillage dont les côtés des carreaux mesurent 1 cm. Cela faciliterait-il le placement des points M et N sur le segment [LI] ? Pourquoi ?
4) Montrer que l'aire du carré ABCD est le double de l'aire du quadrilatère IJKL.
5) Les aires des triangles ALM, AMN, ANI sont-elles égales ? Justifier.
Question complémentaire (3 points)
1) Quand on demande à des élèves de reproduire la figure précédente sur quadrillage, on peut utiliser différents papiers quadrillés : le papier millimétré, le papier à petits carreaux (côté d'un carreau 5 mm), le papier à grands carreaux (côté d'un carreau 8 mm).
Indiquer, pour chacun de ces types de quadrillage, en quoi il facilite ou non la tâche de l'élève.
Indiquer, pour chacun de ces types de quadrillage, en quoi il facilite ou non la tâche de l'élève.
2) Des prérequis seraient nécessaires si on demandait à des élèves d'effectuer le tracé de cette figure sans quadrillage. En citer trois.
3) Donner une procédure permettant à un élève de cycle 3 de justifier que l'aire du carré ABCD est égale au double de l'aire du quadrilatère IJKL.
Exercice 4 (3 points)
Dans la figure ci-après se trouvent deux graduations régulières d'une même droite, l'une au-dessus (appelée ici « graduation supérieure »), l'autre en dessous (appelée ici « graduation inférieure »).
Par exemple, le nombre 2 de la graduation supérieure correspond au nombre 14 de la graduation inférieure.
Par exemple, le nombre 2 de la graduation supérieure correspond au nombre 14 de la graduation inférieure.
 |
1) Quel est le nombre de la graduation inférieure correspondant au nombre 12 sur la graduation supérieure ?
Pour les questions suivantes, les réponses seront justifiées.
2) Quel est le nombre de la graduation inférieure correspondant au nombre 2007 sur la graduation supérieure ?
3) Quel est le nombre de la graduation supérieure correspondant au nombre 0 sur la graduation inférieure ?
4) On appelle x un nombre de la graduation supérieure et y le nombre correspondant sur la graduation inférieure. La correspondance entre x et y est donnée par l'égalité x = ay + b. Déterminer a et b.
Annexe
 |
 |
 |
Corrigé
Corrigé
Exercice 1 (3 points)
1) Soient x, x + 1, x + 2, trois nombres entiers consécutifs dont la somme est égale à 207.
On résout l'équation : x + (x + 1) + (x + 2) = 207.
3x + 3 = 207, donc 3(x + 1) = 207, soit x + 1 =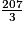 = 69.
= 69.
Les trois nombres entiers consécutifs sont 68, 69 et 70.
On résout l'équation : x + (x + 1) + (x + 2) = 207.
3x + 3 = 207, donc 3(x + 1) = 207, soit x + 1 =
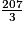 = 69.
= 69.Les trois nombres entiers consécutifs sont 68, 69 et 70.
2) On résout l'équation x + (x + 1) + (x + 2) = 329.
3x + 3 = 329, donc 3(x + 1) = 329, soit x + 1 =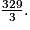
329 n'est pas divisible par 3, donc x + 1 n'est pas un nombre entier. Donc il est impossible de trouver trois nombres entiers consécutifs dont la somme est égale à 329.
3x + 3 = 329, donc 3(x + 1) = 329, soit x + 1 =
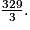
329 n'est pas divisible par 3, donc x + 1 n'est pas un nombre entier. Donc il est impossible de trouver trois nombres entiers consécutifs dont la somme est égale à 329.
3) D'après 1), 207 est la somme de trois nombres entiers consécutifs, car 207 est divisible par 3.
D'après 2), 329 n'est pas la somme de trois nombres entiers consécutifs, car 329 n'est pas divisible par 3.
Caractérisation : un entier n est la somme de trois nombres entiers consécutifs si n est un multiple de 3.
D'après 2), 329 n'est pas la somme de trois nombres entiers consécutifs, car 329 n'est pas divisible par 3.
Caractérisation : un entier n est la somme de trois nombres entiers consécutifs si n est un multiple de 3.
4) 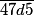 est la somme de trois entiers consécutifs si
est la somme de trois entiers consécutifs si 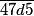 est un multiple de 3, d'après 3).
est un multiple de 3, d'après 3).
Or un nombre est multiple de 3 si la somme de ses chiffres est dans la table de 3.
4 + 7 + d + 5 = 16 + d, et 16 + d est multiple de 3 si d = 2 ou d = 5 ou d = 8.
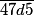 est la somme de trois entiers consécutifs si
est la somme de trois entiers consécutifs si 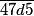 est un multiple de 3, d'après 3).
est un multiple de 3, d'après 3).Or un nombre est multiple de 3 si la somme de ses chiffres est dans la table de 3.
4 + 7 + d + 5 = 16 + d, et 16 + d est multiple de 3 si d = 2 ou d = 5 ou d = 8.
Question complémentaire (5 points)
1) L'élève A procède à tâtons, par tests successifs. Il sait ce qu'on appelle « entiers consécutifs », en choisit trois et pose l'addition des trois nombres choisis. Comme la somme obtenue est trop élevée, il en choisit trois autres, plus petits que les précédents. Leur somme n'étant toujours pas égale à 51, il augmente ensuite de 1 en 1 les trois nombres jusqu'à trouver la bonne réponse.
L'élève B divise 51 par 3 pour obtenir une idée de l'ordre de grandeur de ces trois nombres. Il obtient 17, qu'il choisit comme nombre entier consécutif le plus grand. Il fait la somme de 17 et des deux nombres entiers précédents afin de vérifier s'il obtient une somme de 51. Comme ce n'est pas le cas, il choisit alors 17 comme nombre entier du milieu et trouve alors la bonne réponse.
L'élève C sait ce qu'on appelle « entiers consécutifs », il procède comme l'élève A par tests successifs, mais de façon désordonnée. Par ailleurs, il commet une erreur de retenue quand il pose l'addition de 16, 17 et 18, et donc ne trouve pas de réponse.
L'élève B divise 51 par 3 pour obtenir une idée de l'ordre de grandeur de ces trois nombres. Il obtient 17, qu'il choisit comme nombre entier consécutif le plus grand. Il fait la somme de 17 et des deux nombres entiers précédents afin de vérifier s'il obtient une somme de 51. Comme ce n'est pas le cas, il choisit alors 17 comme nombre entier du milieu et trouve alors la bonne réponse.
L'élève C sait ce qu'on appelle « entiers consécutifs », il procède comme l'élève A par tests successifs, mais de façon désordonnée. Par ailleurs, il commet une erreur de retenue quand il pose l'addition de 16, 17 et 18, et donc ne trouve pas de réponse.
2) La mise en commun a dégagé la pertinence de la méthode de l'élève B. Autoriser la calculatrice permet à tous les élèves d'utiliser cette méthode sur plusieurs nombres en gagnant du temps, en évitant des fautes de calcul comme pour l'élève C. Le but de l'activité est que les élèves se concentrent sur cette méthode et non de vérifier s'ils savent poser des additions et des divisions d'entiers.
Par ailleurs, utiliser la calculatrice dans une 2e phase de l'activité permet de remotiver des élèves qui ne trouvaient pas la réponse avec 51 à cause d'une mauvaise technique opératoire mais qui avaient pourtant compris la consigne.
Par ailleurs, utiliser la calculatrice dans une 2e phase de l'activité permet de remotiver des élèves qui ne trouvaient pas la réponse avec 51 à cause d'une mauvaise technique opératoire mais qui avaient pourtant compris la consigne.
3)
a. L'objectif de cette activité est de montrer que 51, 72 et 54 sont des multiples de 3 et que 91 n'est pas un multiple de 3 puisqu'en divisant 91 par 3, on n'obtient pas un nombre entier.
b. Utiliser la calculatrice permet d'éviter les erreurs de calcul en posant les divisions de 51 par 3, de 72 par 3, etc. Erreurs qui ne permettraient pas à l'élève de caractériser les nombres entiers qui sont la somme de trois entiers consécutifs.
Exercice 2 (2 points)
1)
 |
2) Aire d'un disque = π × rayon2.
A1 = Aire du demi-disque de diamètre [AC] =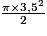 = 6,125π.
= 6,125π.
ABC est un triangle rectangle en B. On applique le théorème de Pythagore : AC2 = AB2 + BC2.
Or ABC est isocèle en B, donc AB = BC, donc AC2 = 2AB2, soit AB2 =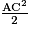 =
= 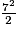 =
= 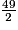 .
.
A2 = Aire du triangle ABC =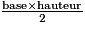 =
= 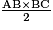 =
= 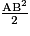 =
= 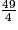 .
.
A3 = Aire des deux demi-disques de diamètre [AB] =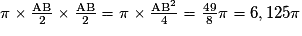 .
.
Aire totale des surfaces grisées = A3 − (A1 − A2) = 6,125π − (6,125π − 12,25) = 12,25 cm2.
A1 = Aire du demi-disque de diamètre [AC] =
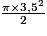 = 6,125π.
= 6,125π.ABC est un triangle rectangle en B. On applique le théorème de Pythagore : AC2 = AB2 + BC2.
Or ABC est isocèle en B, donc AB = BC, donc AC2 = 2AB2, soit AB2 =
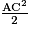 =
= 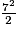 =
= 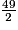 .
.A2 = Aire du triangle ABC =
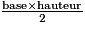 =
= 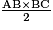 =
= 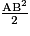 =
= 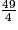 .
.A3 = Aire des deux demi-disques de diamètre [AB] =
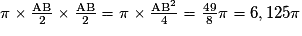 .
.Aire totale des surfaces grisées = A3 − (A1 − A2) = 6,125π − (6,125π − 12,25) = 12,25 cm2.
Exercice 3 (4 points)
1)
a. Les axes de symétrie de cette figure sont les droites (IK), (LJ), (DB) et (AC).
b. L'image du triangle DUK par la symétrie de centre O est le triangle BPI.
2)
a. ABCD est un carré, donc 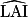 = 90°, c'est-à-dire AIL est rectangle en A.
= 90°, c'est-à-dire AIL est rectangle en A.
ABCD est un carré, donc AB = AD = 6 cm.
I est le milieu de [AB], donc AI =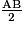 = 3 cm et L est le milieu de [AD], donc AL =
= 3 cm et L est le milieu de [AD], donc AL = 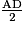 = 3 cm.
= 3 cm.
Donc AIL est isocèle en A.
AIL est donc isocèle rectangle en A.
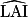 = 90°, c'est-à-dire AIL est rectangle en A.
= 90°, c'est-à-dire AIL est rectangle en A.ABCD est un carré, donc AB = AD = 6 cm.
I est le milieu de [AB], donc AI =
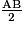 = 3 cm et L est le milieu de [AD], donc AL =
= 3 cm et L est le milieu de [AD], donc AL = 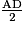 = 3 cm.
= 3 cm.Donc AIL est isocèle en A.
AIL est donc isocèle rectangle en A.
b. AIL est rectangle en A. D'après le théorème de Pythagore, on a IL2 = AL2 + AI2 = 32 + 32 = 18, donc IL = 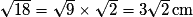 .
.
LM =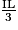 , donc IL =
, donc IL = 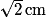 .
.
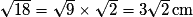 .
.LM =
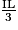 , donc IL =
, donc IL = 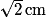 .
.c. IL = 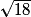 , d'après 2) b. De la même façon, on applique le théorème de Pythagore dans les triangles rectangles IBJ, JCK et KDL. On trouve IL = JK = LK = IL =
, d'après 2) b. De la même façon, on applique le théorème de Pythagore dans les triangles rectangles IBJ, JCK et KDL. On trouve IL = JK = LK = IL = 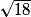 , donc IJKL est un losange.
, donc IJKL est un losange.
De plus,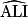 = 45°, car AIL est isocèle rectangle en A et
= 45°, car AIL est isocèle rectangle en A et 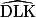 = 45°.
= 45°.
Donc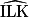 = 180° − (45 + 45) = 90°.
= 180° − (45 + 45) = 90°.
IJKL est un losange qui a un angle droit, donc IJKL est un carré.
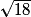 , d'après 2) b. De la même façon, on applique le théorème de Pythagore dans les triangles rectangles IBJ, JCK et KDL. On trouve IL = JK = LK = IL =
, d'après 2) b. De la même façon, on applique le théorème de Pythagore dans les triangles rectangles IBJ, JCK et KDL. On trouve IL = JK = LK = IL = 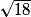 , donc IJKL est un losange.
, donc IJKL est un losange.De plus,
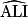 = 45°, car AIL est isocèle rectangle en A et
= 45°, car AIL est isocèle rectangle en A et 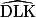 = 45°.
= 45°.Donc
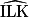 = 180° − (45 + 45) = 90°.
= 180° − (45 + 45) = 90°.IJKL est un losange qui a un angle droit, donc IJKL est un carré.
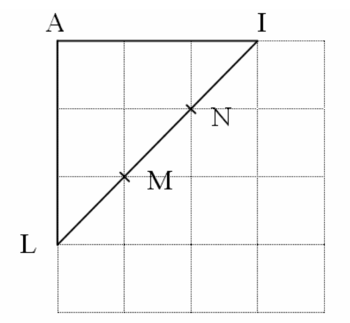
3) En utilisant un quadrillage dont les côtés des carreaux mesurent 1 cm, on observe ci-dessous qu'il est alors facile de diviser le segment [LI] en trois segments de même longueur.
On a LM = MN = NI = diagonale d'un carreau.
On a LM = MN = NI = diagonale d'un carreau.
 |
4) Aire de ABCD = côté × côté = 6 × 6 = 36 cm2.
Aire de IJKL = côté × côté =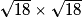 = 18 cm2.
= 18 cm2.
Donc Aire de ABCD = 2 × Aire de IJKL.
Aire de IJKL = côté × côté =
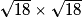 = 18 cm2.
= 18 cm2.Donc Aire de ABCD = 2 × Aire de IJKL.
5) AL = AI, AM = AN et LM = NI, donc ALM et ANI sont des triangles isométriques, donc Aire de ALM = Aire ANI.
Par ailleurs, montrons que les aires des triangles AMN et ALM sont aussi égales.
Soit H le pied de la hauteur du triangle AIL issue de A.
Aire du triangle ALM =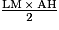
Aire du triangle AMN =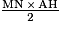
Or LM = MN, donc Aire de ALM = Aire de AMN.
On en déduit que Aire de ALM = Aire de AMN = Aire de ANI.
Par ailleurs, montrons que les aires des triangles AMN et ALM sont aussi égales.
Soit H le pied de la hauteur du triangle AIL issue de A.
Aire du triangle ALM =
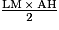
Aire du triangle AMN =
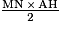
Or LM = MN, donc Aire de ALM = Aire de AMN.
On en déduit que Aire de ALM = Aire de AMN = Aire de ANI.
Question complémentaire (3 points)
1) Utiliser le papier à petits carreaux permet de placer très facilement, en s'aidant des carreaux, les points M et N sans avoir à mesurer LI ni à diviser la longueur par 3. Il en est de même pour les points P, R, S, T, U et V.
Par contre, le papier millimétré ainsi que le papier à grands carreaux ne permettent pas de placer ces points de façon précise car l'élève va devoir mesurer la longueur LI et la diviser par 3, et donc placer M de façon approximative.
Par contre, le papier millimétré ainsi que le papier à grands carreaux ne permettent pas de placer ces points de façon précise car l'élève va devoir mesurer la longueur LI et la diviser par 3, et donc placer M de façon approximative.
2) Si on demandait à des élèves d'effectuer le tracé de cette figure sans quadrillage, les prérequis suivants seraient nécessaires :
- savoir manier l'équerre et la règle ;
- savoir prendre le milieu d'un segment ;
- savoir reporter une longueur avec le compas ;
- savoir poser la division d'un nombre décimal par un entier.
3) Pour justifier que l'aire de ABCD est égale au double de l'aire de IJKL, on peut proposer à un élève de cycle 3 de repérer dans ABCD tous les triangles d'aire égale à celle du triangle ALM (les colorier d'une couleur) ainsi que tous ceux d'aire égale à AMN (les colorier d'une autre couleur). Ensuite, on compte tous les triangles de la même couleur et on trouve :
Aire ABCD = 16 × Aire ALM + 8 × Aire AMN,
Aire IJKL = 8 × Aire ALM + 4 × Aire AMN,
donc Aire ABCD = 2 × Aire IJKL.
Aire ABCD = 16 × Aire ALM + 8 × Aire AMN,
Aire IJKL = 8 × Aire ALM + 4 × Aire AMN,
donc Aire ABCD = 2 × Aire IJKL.
Exercice 4 (3 points)
1) Le nombre de la graduation inférieure correspondant au nombre 12 sur la graduation supérieure est 18.
La droite est graduée de 1 en 1 sur la partie supérieure alors que la partie inférieure est graduée de 0,4 en 0,4, car 1 unité correspond à 5 graduations.
Sur la graduation supérieure, 10 + 2 = 12.
La droite est graduée de 1 en 1 sur la partie supérieure alors que la partie inférieure est graduée de 0,4 en 0,4, car 1 unité correspond à 5 graduations.
Sur la graduation supérieure, 10 + 2 = 12.
2) Le nombre de la graduation inférieure correspondant au nombre 2007 sur la graduation supérieure est 816, car le 0 de la graduation supérieure correspond à 13,2 sur la graduation inférieure et 13,2 + 2007 × 0,4 = 816.
3) Le nombre de la graduation supérieure correspondant au nombre 0 sur la graduation inférieure est − 33, car 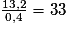 .
.
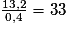 .
.4) On résout le système 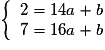 .
.
On soustrait la 2e équation à la 1re, on trouve 5 = 2a, soit a =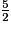 = 2,5.
= 2,5.
On remplace a par 2,5 dans la 1re équation : 2 = 14 × 2,5 + b, soit b = 2 − 14 × 2,5 = − 33
On a l'égalité x = 2,5y − 33.
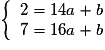 .
.On soustrait la 2e équation à la 1re, on trouve 5 = 2a, soit a =
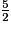 = 2,5.
= 2,5.On remplace a par 2,5 dans la 1re équation : 2 = 14 × 2,5 + b, soit b = 2 − 14 × 2,5 = − 33
On a l'égalité x = 2,5y − 33.
