Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
1) Convertir les durées suivantes en secondes :
a. deux tiers d'heure.
b. 1,2 heure.
2) Convertir les durées suivantes en heures, minutes et secondes :
a. 5 532 secondes.
b. 1,87 heure.
3) Quelle durée faut-il à la grande aiguille d'une montre pour parcourir un angle de 54° ?
4) Depuis sa position initiale à midi pile, la petite aiguille d'une montre a parcouru un angle de 68°. Quelle est la nouvelle heure indiquée ?
5) Arnaud part de Paris à 23h00 pour Rio de Janeiro. Son avion se pose à Houston à 03h00 (heure locale) pour une escale d'une heure. Le vol entre Houston et Rio de Janeiro dure 10 heures.
Houston est à l'ouest de Paris et il y a 7 heures de décalage horaire entre ces deux villes.
Rio de Janeiro est à l'est de Houston et il y a 3 heures de décalage horaire entre ces deux villes.
Houston est à l'ouest de Paris et il y a 7 heures de décalage horaire entre ces deux villes.
Rio de Janeiro est à l'est de Houston et il y a 3 heures de décalage horaire entre ces deux villes.
a. Quelle est la durée du vol entre Paris et Houston ?
b. À quelle heure (heure locale) Arnaud arrive-t-il à Rio de Janeiro ?
Question complémentaire (4 points)
L'énoncé de problème suivant a été proposé à des élèves dont la production est en annexe 1.
« Je suis parti à neuf heures moins dix ; je suis arrivé à 10h40. Quelle a été la durée de mon parcours ? Explique comment tu as trouvé. »
1) Indiquer le cycle et le niveau de classe auxquels cet énoncé peut être proposé.
2) Quelles raisons didactiques ont pu motiver le choix des heures et de leurs expressions retenu dans l'énoncé ?
3) Pour chacune des productions d'élèves reproduites dans l'annexe 1, décrire la procédure utilisée et analyser les erreurs éventuellement commises en formulant des hypothèses sur leurs origines.
4) Quels supports et/ ou outils peuvent aider à la résolution de cet exercice ?
Exercice 2 (4 points)
1) Pour cette question, tracer sur la copie une figure ressemblant à celle de l'annexe 2.
Il ne s'agit pas de reproduire exactement cette figure mais d'en respecter la forme et la disposition.
Construire à la règle et au compas les symétriques A', B' et C' des points A, B et C par rapport à la droite (OI) en laissant apparents les traits de construction.
Construire à la règle et au compas les symétriques A'', B'' et C'' des points A', B' et C' par rapport à la droite (OJ) en laissant apparents les traits de construction.
Il ne s'agit pas de reproduire exactement cette figure mais d'en respecter la forme et la disposition.
Construire à la règle et au compas les symétriques A', B' et C' des points A, B et C par rapport à la droite (OI) en laissant apparents les traits de construction.
Construire à la règle et au compas les symétriques A'', B'' et C'' des points A', B' et C' par rapport à la droite (OJ) en laissant apparents les traits de construction.
2) À partir de l'observation de la figure obtenue, donner un argument montrant qu'il n'existe pas de symétrie axiale qui transforme les trois points A, B et C en A'', B'' et C''.
3) Montrer que l'angle 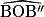 vaut le double de l'angle
vaut le double de l'angle 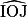 .
.
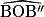 vaut le double de l'angle
vaut le double de l'angle 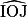 .
.4) Quelle est la transformation du plan qui transforme le triangle ABC en A''B''C'' ? Justifier la réponse.
Question complémentaire (4 points)
Les documents des annexes 3, 4 et 5 sont extraits de « Donner du sens aux mathématiques : tome 1 », M. Fénichel, M. Pauvert, N. Pfaff, Bordas Pédagogie, 2004.
1) Questions concernant la séance 1 (Voir annexe 3 et annexe 4)
L'objectif de la séance 1 est une approche perceptive de la symétrie par rapport à une droite.
a. Dans quel cycle cette séance peut-elle être proposée ?
b. Dans la phase 2, pourquoi les élèves « ne disposent-ils d'aucun matériel » ?
c. Dans la phase 3, il est indiqué que « cette mise en commun doit faire apparaître des arguments pour dire à quelle condition on obtient un papillon ». Selon vous, quels arguments le maître souhaite-t-il mettre en valeur ?
d. Dans la phase 4, comment les élèves peuvent-ils valider les réponses obtenues après la mise en commun ?
2) Questions concernant la séance 2 (Voir annexe 3 et annexe 5)
L'objectif de la séance 2 est d'apprendre à identifier le symétrique d'une figure donnée en utilisant un papier translucide.
Dans une première phase, le maître laisse les élèves travailler de manière individuelle sur la situation donnée.
a. En quoi cette situation peut-elle montrer les limites des arguments utilisés lors de la séance 1 pour reconnaître les figures symétriques ?
b. Donner une procédure de validation adaptée à cette situation.
Exercice 3 (4 points)
1) Écrire l'égalité caractéristique traduisant la division euclidienne de 1001 par 11.
2) Soit mcdu un nombre à 4 chiffres écrit en base dix. Vérifier que mcdu = 1001 × m + 99 × c + 11 × d − m + c − d + u.
3) a. À partir de la question précédente, énoncer et démontrer un critère de divisibilité par 11 pour les nombres inférieurs à 9999 (condition nécessaire et suffisante).
b. Utiliser ce critère pour trouver trois nombres de quatre chiffres multiples de 11 ayant 38 centaines.
4) a. Montrer que le critère de la question précédente s'applique aussi aux nombres à 6 chiffres qu'on notera abmcdu.
b. Utiliser alors ce critère pour déterminer si le nombre 1,2452 × 1011 est divisible par 11. Justifier la réponse.
Annexes
Annexe 1 : Productions d'élèves
 |
Annexe 2
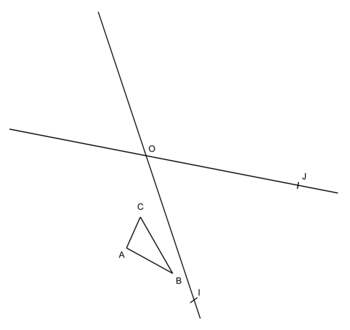 |
Annexe 3 : Les papillons (extrait de description de séances successives)
Séance 1 (Voir « les papillons : annexe 4 »).
Phase 1 : Des photos et des représentations de papillons sont affichées au mur. Les élèves sont invités à décrire pour un papillon les ressemblances, les différences (travail collectif).
Phase 2 : Chaque élève reçoit deux feuilles photocopiées sur lesquelles sont représentées six moitiés de papillons.
Les élèves ne disposent d'aucun matériel.
Sur une feuille, six moitiés gauches de papillons sont numérotées de 1 à 6.
Sur l'autre feuille, six moitiés droites de papillons sont identifiées par des lettres allant de A à F.
La tâche des élèves est d'associer les deux moitiés formant un papillon (travail individuel).
Pour cela les élèves inscrivent, dans un tableau, la lettre correspondant à chaque numéro.
Les élèves ne disposent d'aucun matériel.
Sur une feuille, six moitiés gauches de papillons sont numérotées de 1 à 6.
Sur l'autre feuille, six moitiés droites de papillons sont identifiées par des lettres allant de A à F.
La tâche des élèves est d'associer les deux moitiés formant un papillon (travail individuel).
Pour cela les élèves inscrivent, dans un tableau, la lettre correspondant à chaque numéro.
| Numéro correspondant à la moitié gauche du papillon | Lettre correspondant à la moitié droite du papillon |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 |
Phase 3 : Mise en commun.
Les résultats trouvés sont proposés à la discussion. Il s'agit non pas de faire ressortir la bonne réponse, mais de mettre en évidence, s'il y a lieu, les contradictions entre élèves.
Cette mise en commun doit faire apparaître des arguments pour dire à quelle condition on obtient un papillon.
Les résultats trouvés sont proposés à la discussion. Il s'agit non pas de faire ressortir la bonne réponse, mais de mettre en évidence, s'il y a lieu, les contradictions entre élèves.
Cette mise en commun doit faire apparaître des arguments pour dire à quelle condition on obtient un papillon.
Phase 4 : phase de validation.
Phase 5 : phase d'institutionnalisation. Le maître fait ressortir les éléments importants de la séance et les dicte aux élèves.
Séance 2
Matériel (par élève) :
- une paire de ciseaux ;
- une feuille de papier assez fin sur laquelle sont représentées une moitié gauche de papillon et six moitiés droites de papillon.
La tâche des élèves est de déterminer, parmi les six moitiés droites, celle qui correspond à la moitié gauche du papillon (travail individuel).
Annexe 4 : Les papillons (séance 1)
 |
Annexe 5 : Les papillons (séance 2)
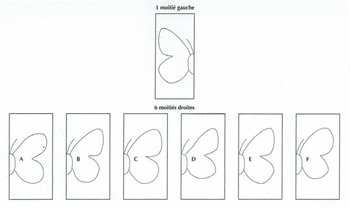 |
Corrigé
Corrigé
Exercice 1 (4 points)
1) a. 1 heure = 3 600 secondes.
2/3 d'heure = 3 600 x 2/3 = 2 400 secondes.
2/3 d'heure = 3 600 x 2/3 = 2 400 secondes.
1) b. 1, 2 heure = 1 heure + 1/5 d'heure.
En convertissant en secondes :
1 heure = 3 600 s ; 1/5 d'heure = 3 600 / 5 = 720 s ;
1,2 heure = 4 320 secondes.
En convertissant en secondes :
1 heure = 3 600 s ; 1/5 d'heure = 3 600 / 5 = 720 s ;
1,2 heure = 4 320 secondes.
2) a. Si on considère que 1 heure = 3 600 secondes, on sait que 5 532 secondes correspondront à une durée comprise entre 1 et 2 heures.
On peut donc dire que 5 532 s = 1 heure et (5 552 − 3 600) secondes, soient 1 heure et 1 932 secondes.
Sachant que 1 minute = 60 secondes, 1 932 ÷ 60 = 32,2 minutes, soient 32 minutes et 1/5 de minute, ou encore, si on considère que 1 minute = 60 secondes, 32 minutes et 12 secondes.
5 532 secondes = 1 heure, 32 minutes et 12 secondes.
On peut donc dire que 5 532 s = 1 heure et (5 552 − 3 600) secondes, soient 1 heure et 1 932 secondes.
Sachant que 1 minute = 60 secondes, 1 932 ÷ 60 = 32,2 minutes, soient 32 minutes et 1/5 de minute, ou encore, si on considère que 1 minute = 60 secondes, 32 minutes et 12 secondes.
5 532 secondes = 1 heure, 32 minutes et 12 secondes.
2) b. 1,87 heure = 1 heure + 1 heure × 0,87.
En effectuant les conversions précédentes :
0,87 × 60 = 52,2 minutes, soient 52 minutes et 1/5 de minute ou encore 52 minutes et 12 secondes ;
1,87 heure = 1 heure 52 minutes et 12 secondes.
En effectuant les conversions précédentes :
0,87 × 60 = 52,2 minutes, soient 52 minutes et 1/5 de minute ou encore 52 minutes et 12 secondes ;
1,87 heure = 1 heure 52 minutes et 12 secondes.
La difficulté de cet exercice est de prendre en compte le système sexagésimal correspondant aux mesures des durées et le système décimal proposé dans le sujet ou obtenu après division par 60.
3) Le tour d'horloge correspond à 360° pour une durée de 60 minutes, lorsqu'il s'agit de la grande aiguille.
Il s'agit d'une situation de proportionnalité.
360° équivaut à 60 minutes ;
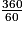 équivaut à 1 minute ;
équivaut à 1 minute ;
6° équivaut à 1 minute ;
6 × 9 = 54 équivaut à 9 minutes.
Il s'agit d'une situation de proportionnalité.
360° équivaut à 60 minutes ;
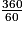 équivaut à 1 minute ;
équivaut à 1 minute ;6° équivaut à 1 minute ;
6 × 9 = 54 équivaut à 9 minutes.
4) La durée effectuée pour un tour de 360° est maintenant de 12 heures, puisqu'il s'agit de la petite aiguille.
360° équivaut à 12 heures ;
1° équivaut à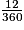 ;
;
68° équivaut à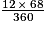 ;
;
soit 2,26 heures ou, en effectuant la démarche précédente, 2 heures et 1/4 d'heure soit 2 heures 15 minutes.
La nouvelle heure indiquée est donc 14 heures 15.
360° équivaut à 12 heures ;
1° équivaut à
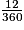 ;
;68° équivaut à
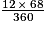 ;
;soit 2,26 heures ou, en effectuant la démarche précédente, 2 heures et 1/4 d'heure soit 2 heures 15 minutes.
La nouvelle heure indiquée est donc 14 heures 15.
5) Au départ d'Arnaud, il est 23 heures à Paris, 16 heures à Houston (7 heures de moins) et 19 heures à Rio (3 heures de plus qu'à Houston ou 4 heures de moins qu'à Paris).
À l'arrivée à Houston, il est 3 heures à Houston, 10 heures à Paris et 6 heures à Rio.
Une heure après l'escale, quand Arnaud repart de Houston, il est 4 heures à Houston, 11 heures à Paris et 7 heures à Rio.
À l'arrivée à Rio, au bout de 10 heures de vol, il est 14 heures à Houston, 21 heures à Paris et 17 heures à Rio. Écrivons ces informations dans un tableau :
À l'arrivée à Houston, il est 3 heures à Houston, 10 heures à Paris et 6 heures à Rio.
Une heure après l'escale, quand Arnaud repart de Houston, il est 4 heures à Houston, 11 heures à Paris et 7 heures à Rio.
À l'arrivée à Rio, au bout de 10 heures de vol, il est 14 heures à Houston, 21 heures à Paris et 17 heures à Rio. Écrivons ces informations dans un tableau :
| Paris | Houston | Rio | |
| Départ Paris | 23 heures | 16 heures | 19 heures |
| Arrivée Houston | 10 heures | 3 heures | 6 heures |
| Départ Houston | 11 heures | 4 heures | 7 heures |
| Arrivée Rio | 21 heures | 14 heures | 17 heures |
a. La durée entre Paris et Houston est le nombre d'heures qui séparent 23 heures de 10 heures ou 16 heures de 3 heures, soit 11 heures.
b. Arnaud arrive à 17 heures à Rio de Janeiro, heure locale.
Question complémentaire (4 points)
1) Cet énoncé peut être proposé au cycle 3, au CE2 ou CM1.
Auparavant, la lecture de l'heure est au programme (sans forcément les finesses du « moins 10 », on privilégiera alors les multiples de 5 ; parfois, on ne traitera que les heures, les demi-heures et les quarts d'heure) mais pas les calculs de durée.
Auparavant, la lecture de l'heure est au programme (sans forcément les finesses du « moins 10 », on privilégiera alors les multiples de 5 ; parfois, on ne traitera que les heures, les demi-heures et les quarts d'heure) mais pas les calculs de durée.
2) Les élèves sont invités à travailler avec les horaires de la journée pendant lesquels ils sont actifs. Ils sont plus faciles à visualiser, – la pendule fait apparaître les heures de 1 à 12 – plus proches de leur vie quotidienne. Par ailleurs, les nombres sont moins importants, la technique opératoire n'étant pas l'objectif de l'exercice.
Les élèves travaillent avec des expressions plutôt utilisées dans la vie courante (neuf heures moins dix plutôt que 8 heures 50) pour les inciter à faire le lien entre ces deux expressions, pour visualiser le principe de tour du cadran, souvent mal compris par des élèves possédant des montres à lecture digitale.
Les élèves travaillent avec des expressions plutôt utilisées dans la vie courante (neuf heures moins dix plutôt que 8 heures 50) pour les inciter à faire le lien entre ces deux expressions, pour visualiser le principe de tour du cadran, souvent mal compris par des élèves possédant des montres à lecture digitale.
3) Mélanie réussit l'exercice, ayant bien compris qu'il fallait prendre en compte les 10 minutes du « neuf heures moins dix » dans la durée à calculer. Kévin le pressent, mais éprouve le besoin d'ajouter les neuf heures à son addition, ce qui permet de penser qu'il ne distingue pas l'heure qu'il est (neuf heures moins dix) de la durée (neuf heures plus dix…minutes ? heures ?).
Sa procédure consiste à surcompter les durées pour aller de l'instant de départ à celui d'arrivée : il y a bien 10 minutes pour aller de neuf heures moins dix à 9 heures, puis une heure et 40 minutes pour aller de 9 heures à 10 heures 40.
Heureusement, le nombre de minutes n'excédait pas 60, la solution est donc trouvée. Toutefois, mathématiquement, il convient de convertir toutes les composantes de l'opération dans la même unité.
Sa procédure consiste à surcompter les durées pour aller de l'instant de départ à celui d'arrivée : il y a bien 10 minutes pour aller de neuf heures moins dix à 9 heures, puis une heure et 40 minutes pour aller de 9 heures à 10 heures 40.
Heureusement, le nombre de minutes n'excédait pas 60, la solution est donc trouvée. Toutefois, mathématiquement, il convient de convertir toutes les composantes de l'opération dans la même unité.
Thomas pose une opération logique, (heure d'arrivée − heure de départ) à ceci près qu'il se trompe dans l'écriture conventionnelle de neuf heures moins dix, qu'il transforme en 9 heures 50 au lieu de 8 heures 50. Comme Mélanie, les unités sont différentes, ce qui le gêne pour faire le calcul. Du coup, il considère le système comme décimal, 10 heures 40 étant assimilé à 1 040 et 9 heures 50 à 950. La différence entre ces deux nombres est bien 90 et la cohérence est respectée dans le choix de l'unité.
Sabrina n'a pas saisi la problématique, et, comme souvent dans ce cas, s'est emparée des données numériques pour les faire entrer dans un schéma connu. Le mot « parcours », a dû être associé à une mesure de longueur, ce qui explique l'unité choisie, le mètre.
Kévin, comme il a été dit plus tôt, a manifestement confondu lecture de l'heure et calcul de durée. Du coup, il ajoute toutes les données, aussi bien le 10 qui peut correspondre à la durée entre 9 heures moins dix et neuf heures, que le 9 ou le 10 de 9 heures moins dix ou dix heures 40. Son résultat final, 69, n'étant pas signifiant pour lui, il lui adjoint 9 heures, ce qui d'une part confirme sa confusion entre heure et durée, et d'autre part montre qu'il ne connaît pas le rapport entre minutes et heures puisque 69 aurait dû lui apparaître équivalent à 1 heure et 9 minutes.
4) Il existe (ou on peut fabriquer avec des attaches parisiennes) des pendules avec des aiguilles manipulables qui permettent de visualiser rapidement les durées. Par ailleurs, on peut marquer, sur ces pendules factices, les équivalences (9 heures moins 10 / 8 heures 50 ; 15 minutes / 1 quart d'heure …ainsi que 11heures / 23 heures). Sur des pendules « jetables » de ce style, on peut alors colorier les durées.
À défaut de tout cela, une horloge murale peut faire l'affaire, pour peu que l'on puisse faire bouger les aiguilles et matérialiser les durées sur une pendule tracée au tableau.
À défaut de tout cela, une horloge murale peut faire l'affaire, pour peu que l'on puisse faire bouger les aiguilles et matérialiser les durées sur une pendule tracée au tableau.
Exercice 2 (4 points)
1)
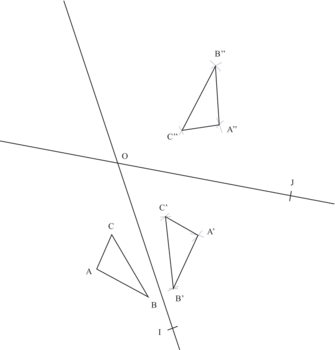 |
2) Les segments AA'', BB'' et CC'' ne sont pas parallèles. Il ne coupent donc pas perpendiculairement une unique droite. Il n'existe pas d'axe par rapport auquel une projection du triangle ABC puisse se réaliser.
3) Le triangle ABC est symétrique au triangle A'B'C' par rapport à la droite (OI).
Le triangle A'B'C' est symétrique au triangle A''B''C'' par rapport à la droite (OJ).
On peut donc écrire que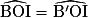 et que
et que 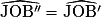 .
.
Le triangle A'B'C' est symétrique au triangle A''B''C'' par rapport à la droite (OJ).
On peut donc écrire que
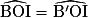 et que
et que 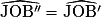 .
.Nous cherchons un rapport entre l'angle 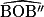 et l'angle
et l'angle 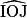 . Or,
. Or,
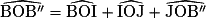
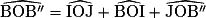
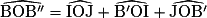
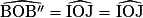
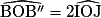
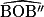 et l'angle
et l'angle 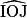 . Or,
. Or,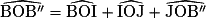
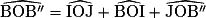
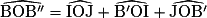
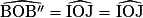
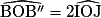
4) Le composé de deux symétries axiales d'axe D1 et D2 sécantes en O est une rotation de centre O. Dans cet exercice, les droites sécantes en O sont (OI) et (OJ).
L'angle de la rotation est alors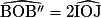
L'angle de la rotation est alors
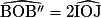
Question complémentaire (4 points)
1) a. Cette phase peut être présentée dès le cycle 2. La notion de symétrie axiale est au programme de ce cycle et cette séance ne requiert pas de compétences particulières en terme de manipulation d'outils.
1) b. Cette phase est préparatoire ; elle est d'abord fondée sur l'observation et non la manipulation qui pourra venir ensuite confirmer ou infirmer les remarques des élèves. C'est une démarche classique qui permet de faire émerger des représentations chez les élèves, puis de les entériner par la preuve.
1) c. Le maître cherche probablement à faire émerger la notion de « ressemblance », de conservation du nombre d'ailes, peut-être de miroir. Il cherche aussi à montrer que le papillon est « coupé » en deux parties superposables, que c'est une ligne droite qui matérialise cette coupure et que de chaque côté de la droite on trouve une moitié de papillon.
Une des difficultés au cycle 2 est de distinguer symétrie et translation et ici, le problème ne se pose pas. Par conséquent, les arguments restent peu nombreux, on travaillera essentiellement sur la forme, le nombre des ailes et la ligne qui sépare les deux moitiés.
1) d. Le maître peut d'abord leur demander comment ils valideraient leurs réponses. Il est probable que les élèves répondraient en proposant d'associer deux parties de papillons, ce qui participe à l'idée qu'il existe un axe commun aux deux parties. Cela faciliterait l'observation, mais ne saurait suffire : il faut que les moitiés de papillons soient parfaitement superposables. Pour le prouver, il faudrait que les moitiés aient été photocopiées sur du papier transparent, que les élèves puissent plier et comparer les formes, ou encore qu'ils utilisent un petit miroir pour comparer la forme obtenue dans le miroir et la moitié à établir.
Il semblerait que les élèves ne disposent de ce matériel que lors de la séance suivante. La validation se fait donc sur une observation argumentée.
2) a. Cette situation, où les élèves disposent au départ de tout ce qui aurait pu servir à valider les réponses de la séance précédente, manifeste que ce matériel était nécessaire. L'observation seule, subjective, n'est pas suffisante. C'est par la preuve et la manipulation que l'on peut vérifier les représentations.
2) b. La validation consiste à faire coïncider les axes de symétrie de la moitié gauche avec chaque moitié droite et de superposer les deux moitiés le long de cet axe unique.
Avant cela, les élèves peuvent même mettre les formes côte à côte pour s'assurer que les corps des papillons ont bien la même dimension verticale. Sur le papier transparent, ils pourront constater l'exacte réplique du « bon » papillon en superposant les moitiés.
Puisqu'il s'agit de forme et qu'il n'y a pas de décoration interne, ils peuvent aussi simplement découper la forme des moitiés de papillons et les superposer.
Puisqu'il s'agit de forme et qu'il n'y a pas de décoration interne, ils peuvent aussi simplement découper la forme des moitiés de papillons et les superposer.
Exercice 3 (4 points)
1) 1001 ÷ 11 = 91.
On peut donc écrire 1001 = 11 × 91.
On peut donc écrire 1001 = 11 × 91.
2) La décomposition canonique d'un nombre de 4 chiffres est la suivante :
mdcu = m × 1000 + c × 100 + d × 10 + u
On peut écrire m × 1000 = m × 1001 − m
c × 100 = c × 99 + c
d × 10 = d × 11 − d
mdcu = m × 1000 + c × 100 + d × 10 + u
On peut écrire m × 1000 = m × 1001 − m
c × 100 = c × 99 + c
d × 10 = d × 11 − d
mdcu peut alors s'écrire sous la forme :
m × 1001 − m + c × 99 + c + d × 11 − d + u
1001 × m + 99 × c + 11 × d − m + c − d + u
m × 1001 − m + c × 99 + c + d × 11 − d + u
1001 × m + 99 × c + 11 × d − m + c − d + u
3) a. Nous avons montré (question 1) que 1001 était un multiple de 11. Par ailleurs, 99 et 11 sont également multiples de 11.
En reprenant l'égalité de la question 2 :
mdcu = 1001 × m + 99 × c + 11 × d − m + c − d + u
mdcu = (11 × 91)m + (11 × 9)c + 11d − m + c − d + u
mdcu = 11(91m + 9c + d) − m + c − d + u
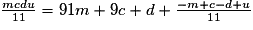
Pour que mdcu soit multiple de 11, il faut donc que − m + c − d + u soit nul ou soit égal à 11. (dans l'absolu, − m + c − d + u peut être n'importe quel multiple de 11, mais chaque lettre représentant 1 chiffre compris entre 0 et 9, on ne peut pas écrire de multiple de 11 supérieur à 11 dans ces conditions).
En reprenant l'égalité de la question 2 :
mdcu = 1001 × m + 99 × c + 11 × d − m + c − d + u
mdcu = (11 × 91)m + (11 × 9)c + 11d − m + c − d + u
mdcu = 11(91m + 9c + d) − m + c − d + u
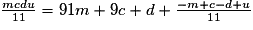
Pour que mdcu soit multiple de 11, il faut donc que − m + c − d + u soit nul ou soit égal à 11. (dans l'absolu, − m + c − d + u peut être n'importe quel multiple de 11, mais chaque lettre représentant 1 chiffre compris entre 0 et 9, on ne peut pas écrire de multiple de 11 supérieur à 11 dans ces conditions).
3) b. Considérons le nombre à 4 chiffres 38du.
Pour que ce nombre soit divisible par 11, il faut et il suffit que :
Plusieurs nombres sont alors possibles :
3894
3883
3839
Pour que ce nombre soit divisible par 11, il faut et il suffit que :
| −m + c − d + u = 0 | ou | −m + c − d + u = 11 |
| −3 + 8 − d + u = 0 | ou | −3 + 8 − d + u = 11 |
| 5 − d + u = 0 | ou | 5 − d + u = 11 |
| 5 = d − u | ou | u − d = 6 |
Plusieurs nombres sont alors possibles :
3894
3883
3839
4) a. Le critère précédent faisait apparaître, pour un nombre de 4 chiffres, que la décomposition canonique classique mdcu = m × 1000 + c × 100 + d × 10 + u pouvait s'écrire de la manière suivante : mdcu = 1001 × m + 99 × c + 11 × d − m + c − d + u, utilisant le principe suivant :
Selon le même principe, en alternant selon le rang,
xa − a avec x − 1 = 102n+1 et by + y avec y + 1 = 102n on obtient, pour un nombre de 6 chiffres :
abmdcu = 100001m + 9999c + 1001m + 99c + 11d − a + b − m + c − d + u.
| 1000m = 1001m − m | | 103m = (103 + 1)m − m |
| 100c = 99c + c | | 102c = (102 − 1)c + c |
| 10u = 11d − d | | 101 d = (101 + 1)d − d |
Selon le même principe, en alternant selon le rang,
xa − a avec x − 1 = 102n+1 et by + y avec y + 1 = 102n on obtient, pour un nombre de 6 chiffres :
abmdcu = 100001m + 9999c + 1001m + 99c + 11d − a + b − m + c − d + u.
100 001 est un multiple de 11 (100 001 = 11 × 9091).
Pour que abmcdu soit divisible par 11, il faut et il suffit que − a + b − m + c − d + u = 0 ou soit un multiple de 11 (11 ou 22). Du reste, ce critère s'applique bien à 100 001…
Pour que abmcdu soit divisible par 11, il faut et il suffit que − a + b − m + c − d + u = 0 ou soit un multiple de 11 (11 ou 22). Du reste, ce critère s'applique bien à 100 001…
4) b. 1,2452 x 1011 = 124 520 × 106
Si 124 520 est divisible par 11 alors 124 520 × 106 est divisible par 11 aussi.
Il suffit de montrer que 124 520 est divisible par 11, suivant le critère précédent.
Si 124 520 est divisible par 11 alors 124 520 × 106 est divisible par 11 aussi.
Il suffit de montrer que 124 520 est divisible par 11, suivant le critère précédent.
124 520 = 100 001 + 9 999 × 2 + 1 001 × 4 + 99 × 5 + 11× 2 − 1 + 2 − 4 + 5 − 2
Vérifions la dernière partie de la démarche :
−1 + 2 − 4 + 5 − 2 = 0
Le nombre 124 520 est divisible par 11, par conséquent, 124 520 × 106 est divisible par 11 et 1,2452 × 1011 est divisible par 11.
Vérifions la dernière partie de la démarche :
−1 + 2 − 4 + 5 − 2 = 0
Le nombre 124 520 est divisible par 11, par conséquent, 124 520 × 106 est divisible par 11 et 1,2452 × 1011 est divisible par 11.
