Dernier essai le
- Score :
/20
Sujet
Sujet
Le sujet est composé de cinq exercices indépendants : ci-dessous sont traités les exercices 1 et 2.
Exercice 1
Dans cette version adaptée du biathlon, les élèves ont à parcourir, en courant, 4 grands tours tracés avec des plots sur un stade comme dans la figure ci-dessous. À l'issue de chacun des 3 premiers tours, ils se présentent au pas de tir et lancent 3 balles sur des cibles. S'ils atteignent 3 fois leur cible, ils n'ont pas de pénalité et repartent pour le grand tour suivant. En revanche, pour chaque lancer manqué, ils doivent effectuer un petit tour avant de repartir sur le grand tour.
Pour chaque élève on mesure la durée mise pour faire un parcours complet (grands tours + lancers + petits tours de pénalité le cas échéant). L'objectif est de mettre le moins de temps possible pour effectuer le parcours complet.
Pour chaque élève on mesure la durée mise pour faire un parcours complet (grands tours + lancers + petits tours de pénalité le cas échéant). L'objectif est de mettre le moins de temps possible pour effectuer le parcours complet.
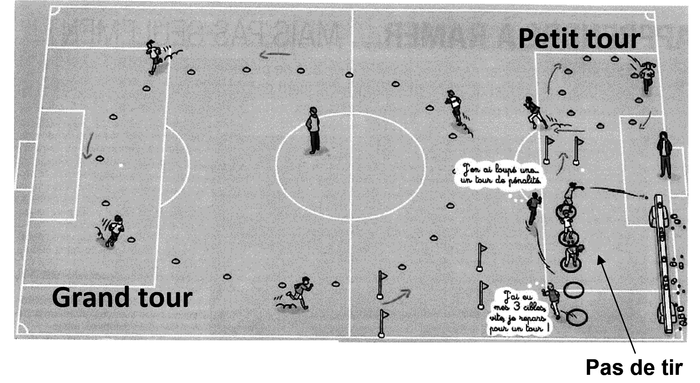 D'après www.revue-eps.com janvier-février-mars 2016 |
Partie 1
Dans cette partie, les élèves s'entraînent à la course sur le grand tour, sans effectuer de lancer de balles.
1. Pour un élève de CE1, la longueur du grand tour est de 250 m.
a. On considère un élève, qui effectue les 4 tours en 10 minutes. Quelle est sa vitesse moyenne de course, en mètre par minute ?
b. Un autre élève a couru les 4 tours à la vitesse moyenne de 150 m/min. Déterminer sa vitesse moyenne en kilomètre par heure.
2. Dans le tableau ci-dessous, les longueurs d'un grand tour pour des élèves de CM1 et de CM2 sont données, ainsi que les temps de course pour effectuer 4 grands tours, de deux élèves (un en CM1 et un en CM2).
| Élève | Longueur de 1 grand tour | Temps de course pour 4 grands tours |
| Élève de CM1 | 400 m | 9 minutes et 30 secondes |
| Élève de CM2 | 500 m | 11 minutes et 8 secondes |
Déterminer la vitesse moyenne (en mètre par minute, arrondie à l'unité) de chacun de ces deux élèves, lorsqu'ils ont réalisé les 4 grands tours.
Partie 2
Dans cette partie, des élèves de CE1 font l'épreuve de biathlon dans sa totalité :
Les 4 grands tours + les 3 épreuves de lancers de 3 balles + les éventuels tours de pénalité.
Les 4 grands tours + les 3 épreuves de lancers de 3 balles + les éventuels tours de pénalité.
On rappelle que pour un élève de CE1, la longueur du grand tour est de 250 m.
1. La longueur du tour de pénalité est de 20 m.
a. Sachant que le tour de pénalité forme un cercle, déterminer son rayon. Arrondir au centimètre.
b. Un élève de CE1, qui court à la vitesse moyenne de 150 m/min, prend le départ de l'épreuve. On suppose que pour effectuer 3 lancers, il passe, à chaque fois, 30 secondes sur le pas de tir.
Quelle sera la durée totale que met cet élève pour réaliser le parcours complet, s'il ne rate aucune cible au premier tour et qu'il rate une cible au 2e tour puis deux cibles au 3e tour ? Donner la réponse en minutes et secondes.
Quelle sera la durée totale que met cet élève pour réaliser le parcours complet, s'il ne rate aucune cible au premier tour et qu'il rate une cible au 2e tour puis deux cibles au 3e tour ? Donner la réponse en minutes et secondes.
2. Le professeur des écoles souhaite aider ses élèves à développer une stratégie pour améliorer leurs résultats. Il relève les performances d'un même élève de CE1 qui fait 3 fois l'épreuve de biathlon dans sa totalité en modifiant certains paramètres à chaque essai. Dans le tableau ci-dessous, Vmoy est la vitesse moyenne de cet élève sur les périodes de course (4 grands tours + éventuels tours de pénalités).
 |
a. La formule saisie en H3 puis recopiée vers le bas est
=1 000+(C3+E3+G3)*20.
Expliquer le terme (C3+E3+G3)*20 dans le contexte de l'exercice.
=1 000+(C3+E3+G3)*20.
Expliquer le terme (C3+E3+G3)*20 dans le contexte de l'exercice.
b. Donner une formule qui pourra être introduite dans la cellule J3, de telle sorte qu'elle puisse être recopiée vers le bas pour effectuer le calcul pour les autres essais.
c. Donner une formule qui pourra être introduite dans la case « durée totale » K3, de telle sorte qu'elle puisse être recopiée vers le bas pour effectuer le calcul pour les autres essais.
Après calculs, on obtient le tableau complet ci-dessous :
 |
d. Interpréter le tableau pour déterminer ce que l'élève a modifié entre l'essai 2 et l'essai 3.
e. Si on analyse les performances de l'élève aux essais 2 et 3, quelle hypothèse ce tableau permet-il de faire du point de vue des stratégies à adopter ?
Exercice 2
On dispose d'un dé cubique non truqué dont les faces opposées sont identiques : deux faces numérotées 0, deux faces numérotées 1 et deux faces numérotées 2.
1. On effectue deux lancers et on lit, à chaque lancer, le chiffre inscrit sur la face supérieure. Les deux lancers permettent d'obtenir un nombre décimal : le résultat du premier lancer donne le chiffre des unités et celui du second lancer le chiffre des dixièmes.
a. Donner la liste de tous les nombres que l'on peut obtenir.
b. Justifier que la probabilité d'obtenir 1,2 est égale à 1/9.
c. Quelle est la probabilité d'obtenir un nombre strictement inférieur à 1 ?
d. Quelle est la probabilité d'obtenir un nombre entier ?
e. Quelle est la probabilité d'obtenir un nombre décimal ?
2. Le tapis représenté ci-contre est constitué de 36 carrés de côté 10 cm.
Ces carrés définissent trois zones Z1, Z2 et Z3 repérées par des couleurs différentes.
Ces carrés définissent trois zones Z1, Z2 et Z3 repérées par des couleurs différentes.
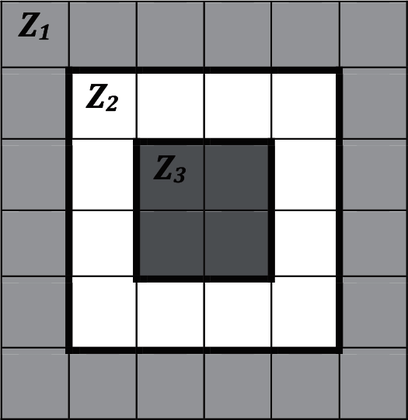 |
Avec le même dé que précédemment, on effectue un lancer sur ce tapis et on regarde la face supérieure. Si le dé tombe à cheval sur deux zones, on le relance. On admet que la probabilité que le dé tombe dans une zone est proportionnelle à l'aire de la zone.
a. Quelle est la probabilité que le dé tombe dans la zone Z2 ?
b. Quelle est la probabilité que le dé tombe en zone Z2 et donne le nombre 1 ?
c. Quelle est la probabilité que le dé tombe en zone Z2 et donne un nombre pair ?
Corrigé
Corrigé
Exercice 1
Partie 1
Course uniquement sur le grand tour.
1. CE1 : longueur du grand tour 250 m.
a. Il parcourt 4 tours en 10 minutes soit 4 × 250 m = 1000 m en 10 min soit en moyenne 100 m en 1 min, donc sa vitesse est de 100 m/min
b. Sa vitesse est de 150 m/min, donc il parcourt 150 m en moyenne en 1 min, donc 150 m × 60 en 60 min soit 9000 m/h = 9 km/h
Remarque : on pouvait aussi appliquer la formule 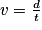
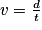
2. On sait que la vitesse moyenne est égale au quotient à la distance parcourue par le temps de parcours.
L'élève de CM1 parcourt 4 tours de 400 m en 9 min 30 s soit 1 600 m en 9,5 min, donc sa vitesse moyenne est de 1 600 : 9,5 m/min, soit environ 168 m/min.
L'élève de CM1 parcourt 4 tours de 400 m en 9 min 30 s soit 1 600 m en 9,5 min, donc sa vitesse moyenne est de 1 600 : 9,5 m/min, soit environ 168 m/min.
L'élève de CM2 parcourt 4 tours de 500 m en 11 min 8 s soit 2 000 m en (11+8/60) min, donc sa vitesse moyenne est de 1 600 : (11 + 8/60) m/min, soit environ 180 m/min.
Partie 2
1.
a. La longueur du tour de pénalité est de 20 m soit 2 000 cm. O, sait que la longueur l d'un cercle de rayon r est donnée par la formule 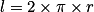 , donc
, donc
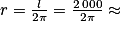 318 cm.
318 cm.
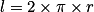 , donc
, donc 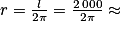 318 cm.
318 cm.b. L'élève court à la vitesse moyenne de 150 m/mi, donc il parcourt les 4 grands tours de 250 m et 3 tours de pénalité de 20 m, donc en tout 1060 m soit pendant 
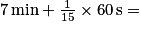 7 min 4 s
7 min 4 s
Comme il passe 30 s sur le pas de tir à chacun de ses lancers soit 90 s = 1 min 30 s en tout.
Sa durée totale est donc de 7 min 4 s + 1 min 30 s = 8 min 34 s.

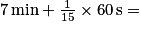 7 min 4 s
7 min 4 sComme il passe 30 s sur le pas de tir à chacun de ses lancers soit 90 s = 1 min 30 s en tout.
Sa durée totale est donc de 7 min 4 s + 1 min 30 s = 8 min 34 s.
2.
a. L'élève parcourt 4 grands tours, soit une distance de 4 × 250 m = 1 000 m d'où le 1 000 dans la formule ; il manque au premier essai C3 cibles, au deuxième essai E3 cibles et au troisième essai G3 cibles, donc parcourt C3 + E3 + G3 tours de pénalité de 20 m chacun soit une distance totale en mètres de 1 000 + (C3 + E3 + G3)* 20.
b. On cherche la vitesse moyenne de course, donc on divise la distance totale parcourue par le temps de cours exprimé en min.
On tape donc la formule = H3/(I3/60), puisque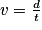 et qu'il faut convertir en minutes le temps exprimées en secondes.
et qu'il faut convertir en minutes le temps exprimées en secondes.
On tape donc la formule = H3/(I3/60), puisque
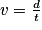 et qu'il faut convertir en minutes le temps exprimées en secondes.
et qu'il faut convertir en minutes le temps exprimées en secondes.c. La durée totale est la somme du temps de course et des sommes des durées au stand de tir : on pourra donc entrer la formule = (B3 + D3 + F3 + I3) / 60
d. On remarque dans ce deuxième tableau que les temps de courses sont différents du premier tableau. Entre l'essai 2 et l'essai 3, l'élève a considérablement raccourci sa durée au stand de tir, ce qui lui a fait rater plus de tirs et l'a obligé à faire des tours de pénalité, donc à parcourir une plus grande distance et finalement à augmenter la durée totale de son parcours.
e. L'objectif étant de réduire au maximum la durée totale de son parcours, mieux vaut prendre son temps pour lancer afin de ne pas rater de cible.
Exercice 2
1.
a. On peut obtenir les neuf nombres : 0 ; 0,1 ; 0,2 ; 1 ; 1,1 ; 1,2 ; 2 ; 2,1 ; 2,2.
b. Les deux lancers étant indépendants, la probabilité d'obtenir 1,2 est le produit des probabilités d'obtenir 1 au premier lancer (deux faces sur les 6 portent le chiffre 1) et 2 au deuxième lancer (deux faces sur les 6 portent le chiffre 1), soit :
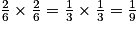
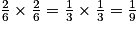
c. La probabilité d'obtenir un nombre strictement inférieur à 1 est la probabilité d'obtenir 0 ou 0,1 ou 0,2 soit 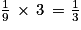
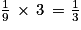
d. La probabilité d'obtenir un nombre entier est la probabilité d'obtenir 0 ou 1 ou 2, soit 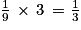
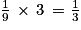
e. On est certain d'obtenir un nombre décimal (les nombres entiers étant des décimaux particuliers), donc la probabilité d'obtenir un nombre décimal est égale à 1.
2.
Calcul de l'aire des 3 zones :
Aire (Z1) = 20 x 102 cm2 = 2 000 cm2
Aire (Z2) = 12 x 102 cm2 = 1 200 cm2
Aire (Z3) = 4 x 102 cm2 = 400 cm2
L'aire du grand carré est égale à 36 × 102 cm2 = 3 600 cm2.
Aire (Z1) = 20 x 102 cm2 = 2 000 cm2
Aire (Z2) = 12 x 102 cm2 = 1 200 cm2
Aire (Z3) = 4 x 102 cm2 = 400 cm2
L'aire du grand carré est égale à 36 × 102 cm2 = 3 600 cm2.
a. La probabilité que le dé tombe dans la zone Z2 est de 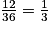
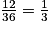
b. La probabilité que le dé tombe dans la zone Z2 et donne le nombre 1 (ces deux événements étant indépendants) est égale à 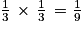
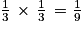
c. La probabilité que le dé tombe dans la zone Z2 et donne un nombre pair (donc soit 0, soit 2) est égale à 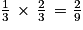
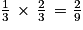
Document précédent
Sujet 2022 de mathématiques, groupement académique 2 — Exercices 1 et 2
