Dernier essai le
- Score :
/20
Sujet
Sujet
Première partie (13 points)
Dans cette partie, on cherche à optimiser la quantité de métal nécessaire à la fabrication de canettes de 33 centilitres (cL).
A. Canette « classique »
On modélise une « canette classique » par le cylindre de révolution représenté ci-dessous. Le volume d'un tel cylindre s'obtient en multipliant l'aire de sa base par sa hauteur.
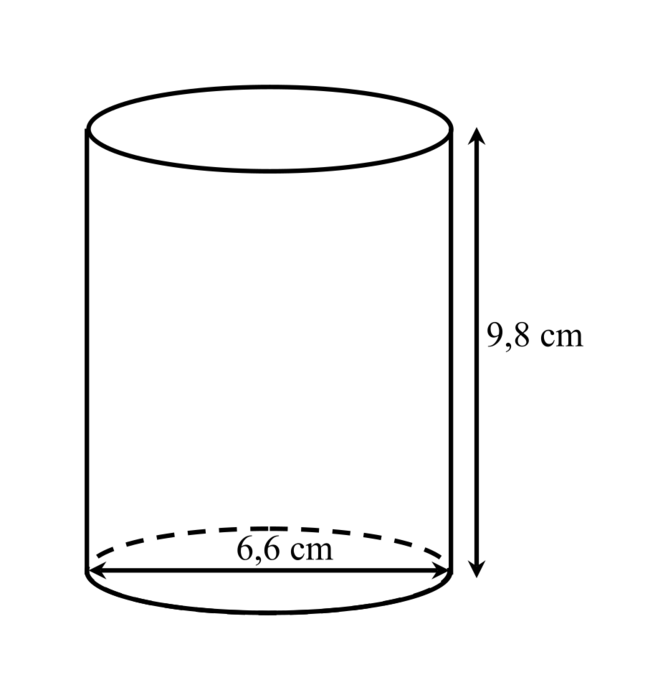 |
Vérifier que le volume de ce cylindre, de diamètre 6,6 cm et de hauteur 9,8 cm, est supérieur à 33 cL.
B. Canette « slim »
Un nouveau format de canette est apparu dernièrement sur le marché. Ces canettes allongées, dites « slim », sont plus hautes et plus fines que les précédentes, pour une même contenance.
Le cylindre représenté ci-dessous en modélise une. Son diamètre est de 5,6 cm.
Le cylindre représenté ci-dessous en modélise une. Son diamètre est de 5,6 cm.
 |
Déterminer au millimètre près la plus petite hauteur possible du cylindre pour que la canette contienne au moins 33 cL.
C. Étude du lien entre le rayon de la base d'une canette de 33 cL et l'aire de son patron
On appelle r le rayon, en centimètres, de la base du cylindre modélisant une canette de 33 cL et h sa hauteur, en centimètres.
1. Vérifier que h = 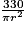 .
.
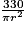 .
.2.
La figure ci-dessous représente le patron du cylindre. Celui-ci est formé de deux disques, et d'un rectangle de largeur h et de longueur L, exprimées en centimètres.
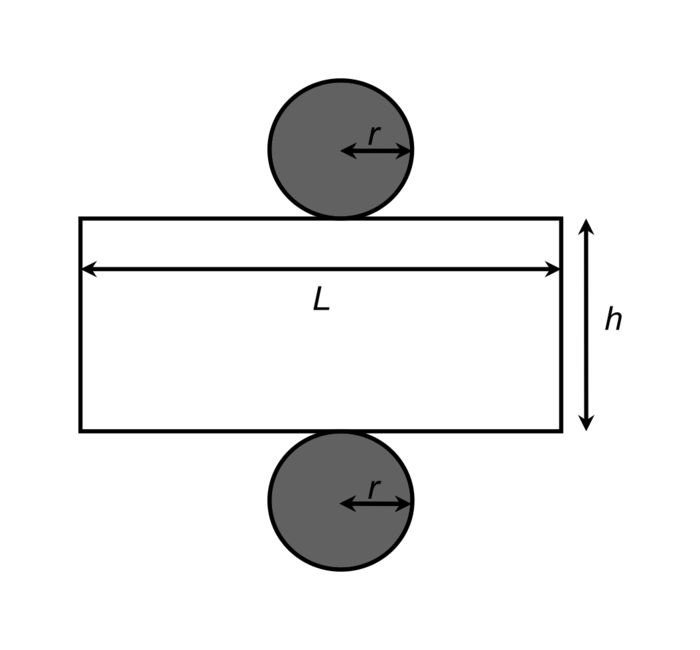 Cette figure n'est pas à l'échelle. |
Exprimer la longueur L en fonction de r.
3. Vérifier que l'aire, en centimètres carrés, de la partie rectangulaire du patron est 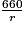 .
.
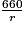 .
.4. Exprimer l'aire totale A du patron du cylindre, en centimètres carrés, en fonction de r.
D. Lecture graphique
On s'intéresse à la réalisation d'un cylindre de révolution de base de rayon r, exprimé en centimètres, et de contenance 33 cL. L'aire, exprimée en centimètres carrés, de la surface de métal nécessaire est modélisée par la fonction f qui, à tout nombre r strictement positif, associe f(r) = 2πr2 + 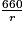 .
.
La fonction f est représentée ci-dessous.
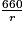 .
.La fonction f est représentée ci-dessous.
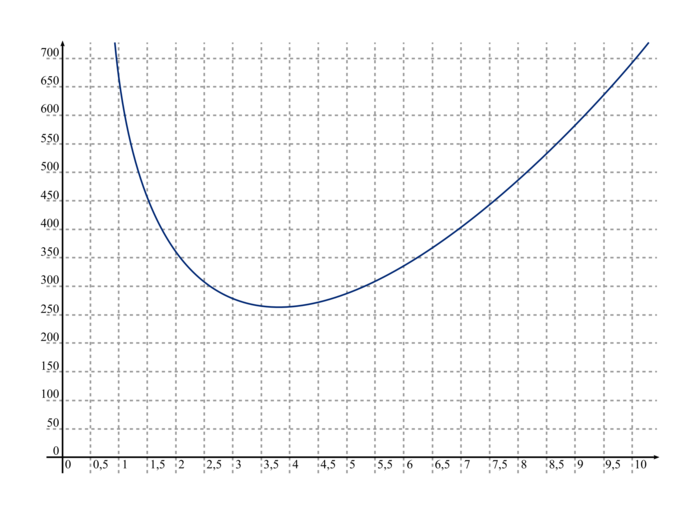 |
Répondre par lecture graphique aux questions suivantes.
1. Quelle est l'aire de la surface de métal nécessaire pour un cylindre dont la base a pour rayon 1,5 cm ?
2. À quelle(s) valeur(s) du rayon du cylindre correspond une aire de 300 cm2 ?
3. Déterminer laquelle de la canette « classique » ou de la canette « slim » utilise le moins de surface de métal pour sa réalisation. Justifier la réponse en donnant les lectures graphiques effectuées.
4. À quelle valeur du rayon correspond la surface minimale de métal nécessaire à la fabrication d'une canette de 33 cL ?
E. Utilisation d'un tableur
On souhaite, à l'aide d'un tableur, affiner la réponse obtenue à la question D.4. par lecture graphique.
Voici une copie d'écran de la feuille de calcul utilisée :
Voici une copie d'écran de la feuille de calcul utilisée :
 |
1. Écrire une formule qui, entrée dans la cellule B2 et étirée vers la droite, permet d'obtenir les valeurs de f(r) sur la ligne 2.
Note : la fonction PI() du tableur renvoie la valeur de π avec une précision de 15 décimales.
Note : la fonction PI() du tableur renvoie la valeur de π avec une précision de 15 décimales.
2. Utiliser cette feuille de calcul pour déterminer un encadrement, le plus précis possible, du rayon du cylindre permettant de minimaliser l'aire de la surface de métal nécessaire à la réalisation d'une canette de 33 cL.
3. Déterminer la hauteur de la canette de 33 cL ayant une base de rayon 3,7 cm. Arrondir le résultat au dixième de centimètre.
F.
Les canettes sont fabriquées à partir d'une feuille plane de tôle d'aluminium d'épaisseur 130 micromètres (μm). Un micromètre est égal à un millionième de mètre. La masse volumique de l'aluminium est 2 700 kg/m3.
On s'intéresse aux canettes classiques dont le rayon est de 3,3 cm et dont la surface de métal nécessaire est de 268,42 cm2, selon le tableau précédent.
On admet que l'anneau pour ouvrir la canette et le rivet de liaison entre l'anneau et le couvercle ont une masse de 1,4 g et que la masse d'aluminium nécessaire pour souder le couvercle au reste de la canette est 1,9 g.
On s'intéresse aux canettes classiques dont le rayon est de 3,3 cm et dont la surface de métal nécessaire est de 268,42 cm2, selon le tableau précédent.
On admet que l'anneau pour ouvrir la canette et le rivet de liaison entre l'anneau et le couvercle ont une masse de 1,4 g et que la masse d'aluminium nécessaire pour souder le couvercle au reste de la canette est 1,9 g.
1. Déterminer, au dixième de gramme près, la masse d'aluminium nécessaire pour fabriquer une canette classique.
2. Il faut 9 kg d'aluminium pour fabriquer un certain type de vélo. Estimer le nombre de canettes classiques nécessaires pour obtenir l'aluminium pour fabriquer un tel vélo.
Deuxième partie (13 points)
Cette partie est composée de quatre exercices indépendants.
Exercice 1
Les informations présentées dans cet exercice sont extraites du site de l'Établissement français du sang qui gère le don du sang en France (https:/www.dondusang.net/).
 |
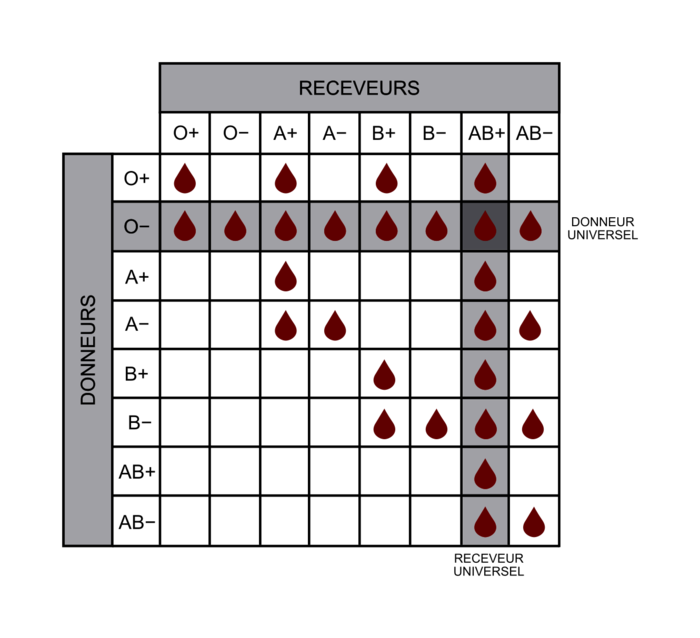 |
Lecture : une personne de groupe A rhésus négatif (A−) peut recevoir du sang d'un donneur du groupe O rhésus négatif ou du groupe A rhésus négatif. Il peut donner son sang à des personnes des groupes et rhésus A+ ; A− ; AB+ et AB−.
1. Quelle est la probabilité qu'une personne choisie au hasard dans la population française soit « donneur universel » ?
2. Quelle est la probabilité qu'une personne choisie au hasard dans la population française soit « receveur universel » ?
3. Quelle est la probabilité qu'une personne choisie au hasard dans la population française puisse donner son sang à une personne du groupe B, rhésus + ?
4. On choisit au hasard une personne parmi les personnes du groupe O dans la population française. Quelle est la probabilité que cette personne soit « donneur universel » ? Arrondir le résultat au centième.
Au 1er janvier 2016, d'après l'Insee, la population française était de 66 627 602 personnes. Parmi ces personnes, 43 217 325 personnes avaient entre 18 et 70 ans, critère requis pour pouvoir donner son sang.
5. Estimer le nombre de « donneurs universels » en France au 1er janvier 2016.
6. Quel pourcentage de la population française représentait, au 1er janvier 2016, la population susceptible de donner son sang ?
Exercice 2
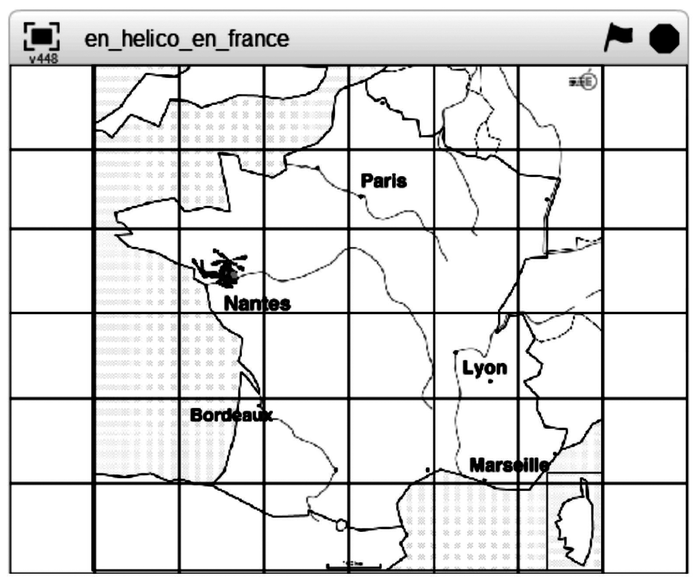 |
Le programme ci-dessous a été écrit avec le logiciel Scratch pour faire se déplacer le lutin « hélicoptère » de la case « Nantes » à la case « Paris » sur l'arrière-plan ci-dessus, c'est-à-dire pour « avancer » de deux cases et « monter » d'une case.
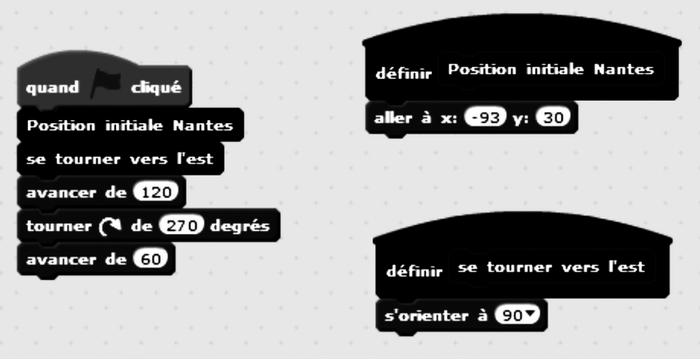 |
Un élève souhaite modifier le programme pour que l'hélicoptère se déplace de la case « Nantes » à la case « Lyon ». Par quels nombres doit-il remplacer les nombres « 120 », « 270 » et « 60 » ? Justifier votre réponse.
Exercice 3
Pour calculer de tête le carré d'un nombre entier se terminant par 5 :
- on prend le nombre de dizaines et on le multiplie par l'entier qui suit ce nombre de dizaines, cela donne le nombre de centaines du résultat ;
- on écrit ensuite 25 à droite du nombre de centaines pour obtenir le résultat.
- étape 1 : en calculant 10 × 11 = 110, ce qui donne le nombre de centaines du résultat ;
- étape 2 : on écrit ensuite 25 à droite de 110 pour obtenir le résultat.
1. Montrer comment calculer mentalement 452.
2. Soit n un nombre entier se terminant par 5, n peut s'écrire : 10d + 5 avec d le nombre de dizaines.
Établir la relation :
n2 = 100d(d + 1) + 25.
Établir la relation :
n2 = 100d(d + 1) + 25.
3. Expliquer en quoi le résultat de la question 2 permet d'établir la technique de calcul mental présentée dans l'énoncé.
4. Comment, par extension de la technique de calcul mental présentée, calculer mentalement le carré de 3,5 ?
Exercice 4
ABE est un triangle rectangle en E.
AE = 5 cm et AB = 13 cm.
La droite (BE) et la droite perpendiculaire à (AB) passant par A se coupent en C.
La droite (AE) et la droite perpendiculaire à (AC) passant par C se coupent en D.
AE = 5 cm et AB = 13 cm.
La droite (BE) et la droite perpendiculaire à (AB) passant par A se coupent en C.
La droite (AE) et la droite perpendiculaire à (AC) passant par C se coupent en D.
1. Réaliser la figure en vraie grandeur.
2. Déterminer l'aire du triangle CEA ; on donnera l'arrondi au dixième de mm2.
Troisième partie (14 points)
Cette partie est composée de trois situations indépendantes.
Situation 1
Voici un extrait du programme de l'école maternelle publié dans le Bulletin officiel n° 2 du 26 mars 2015.
| « La stabilisation de la notion de quantité, par exemple trois, est la capacité à donner, montrer, évaluer ou prendre un, deux ou trois et à composer et décomposer deux et trois. Entre deux et quatre ans, stabiliser la connaissance des petits nombres (jusqu'à cinq) demande des activités nombreuses et variées portant sur la décomposition et recomposition des petites quantités […], la reconnaissance et l'observation des constellations du dé, la reconnaissance et l'expression d'une quantité avec les doigts de la main, la correspondance terme à terme avec une collection de cardinal connu. […] Après quatre ans, les activités de décomposition et recomposition s'exercent sur les quantités jusqu'à dix. » |
1. Citer deux procédures qu'un élève de fin de petite section peut utiliser pour affirmer qu'une collection est constituée de trois objets.
2. Proposer une activité à mettre en place en moyenne section pour travailler les décompositions du nombre quatre.
3. Un enseignant de grande section décide d'utiliser avec ses élèves un dé dont les faces sont représentées de la façon suivante :
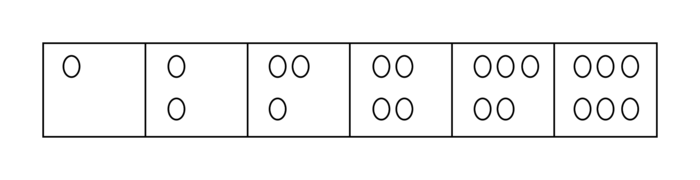 |
Quel intérêt peut-il y avoir à utiliser un tel dé ?
Situation 2
Lors d'un travail sur le calcul en ligne, un enseignant propose la situation suivante à ses élèves : « Calculer 5 × 68 ».
Voici les productions de quatre élèves, Robin, Eléonore, Lucie et Mathys.
Voici les productions de quatre élèves, Robin, Eléonore, Lucie et Mathys.
 |
 |
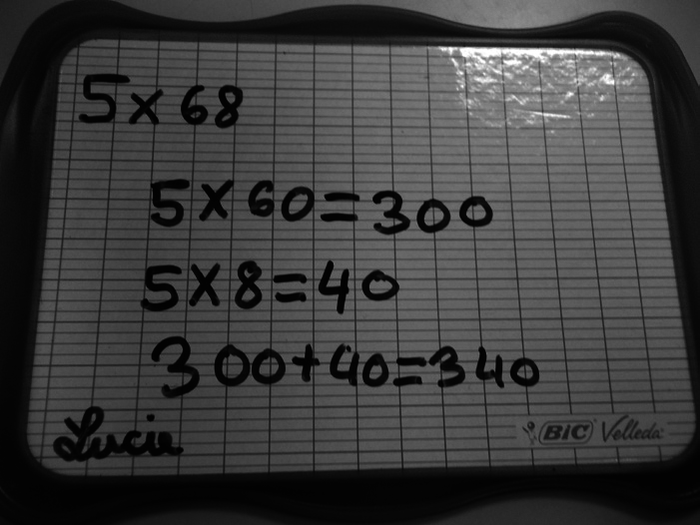 |
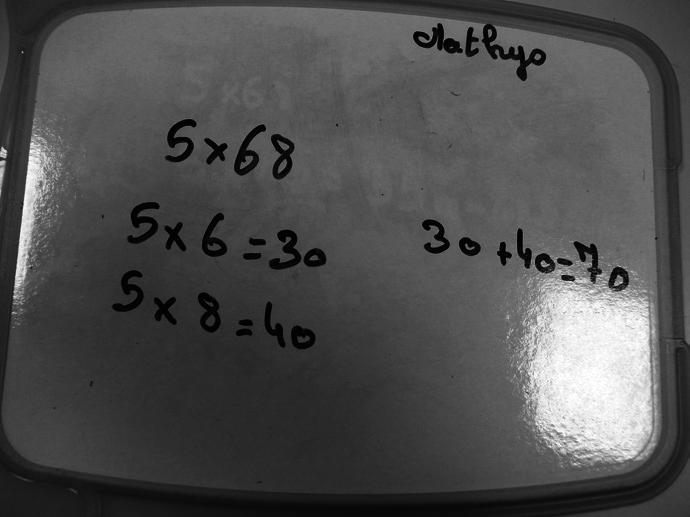 |
1. Analyser chacune des productions, en explicitant les procédures mises en œuvre et en relevant les éventuelles erreurs.
2. Donner trois démarches pouvant être attendues d'un élève de cycle 3 pour calculer en ligne 25 × 28. Pour chacune de ces démarches indiquer les connaissances en jeu.
Situation 3
Un enseignant propose la situation suivante en cycle 3 :
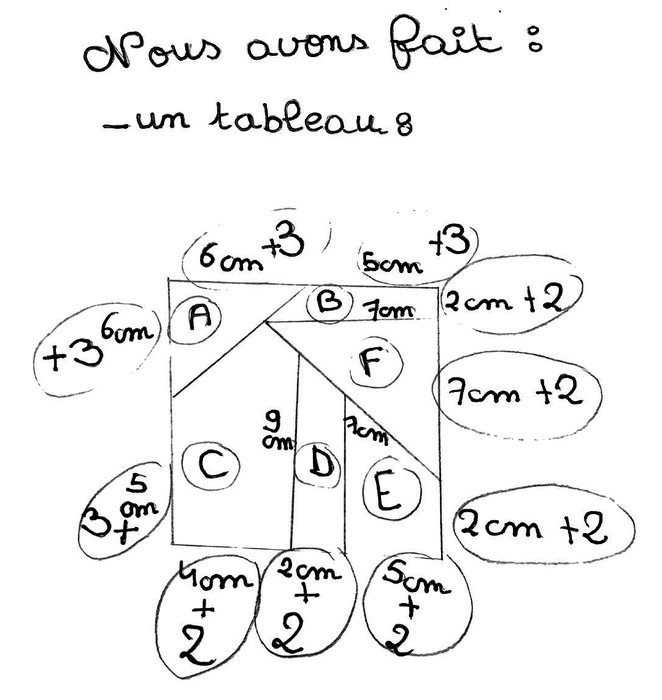
| Consignes données oralement : « Voici un puzzle carré. Vous allez devoir refaire le même puzzle, mais en plus grand. Il faudra le reconstituer exactement avec les pièces agrandies. Le segment de 4 cm devra mesurer 6 cm sur votre puzzle agrandi. Le compte-rendu de vos recherches sera présenté sous la forme d'une affiche. » |
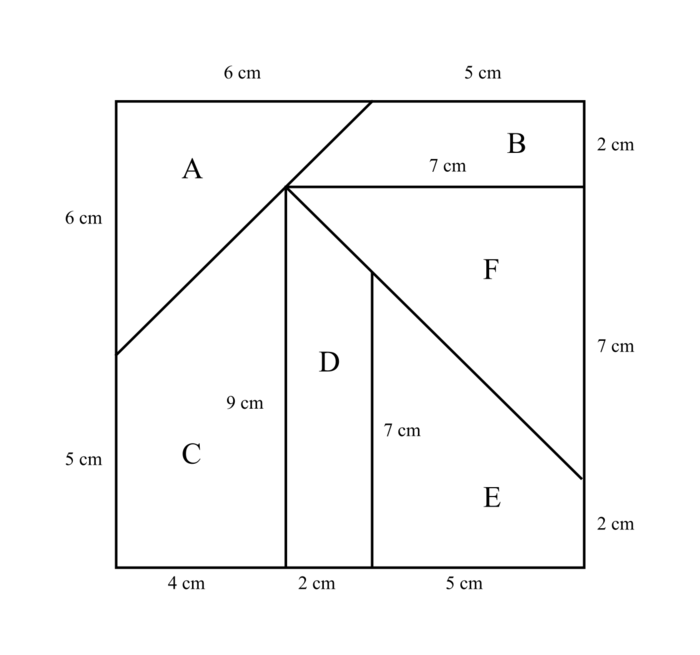 |
Modalités de mise en œuvre : le professeur demande aux élèves de travailler par groupes de quatre, de s'accorder sur la procédure à adopter pour agrandir les éléments du puzzle, de se répartir la construction des pièces en faisant leurs calculs individuellement puis d'assembler les morceaux pour reconstituer le puzzle agrandi.
1. Quel champ mathématique cette situation permet-elle de travailler ?
2. Analyser les différentes stratégies mises en œuvre en pointant les réussites et les erreurs des groupes ayant produit les affiches 1, 2 et 3.
3. Dans la mesure du possible, indiquer les procédures utilisées pour déterminer chacune des valeurs trouvées par le groupe ayant produit l'affiche 4.
 |
 |
 |
 |
Corrigé
Corrigé
Remarque
Dans ce qui suit, le texte en italique constitue des commentaires, que nous espérons formateurs ; il n'a pas à figurer sur une copie.Nous donnons systématiquement un titre à chaque question, titre repris du sujet ou synthétisant le contenu de la question. Ceci n'est pas attendu de la part du candidat le jour de l'épreuve (même si le correcteur appréciera la lisibilité accrue de la copie qui en résulte) ; toutefois, il est profitable pour le candidat de faire cet exercice au moins mentalement, car cela lui permet d'analyser les questions et donc de prendre conscience de leur objectif.
Première partie
A. Volume d'une canette « classique »
Le volume d'un cylindre est donné par la formule :Vcylindre = Abase × h = πr2h, où r est le rayon et h la hauteur du cylindre.
Ici, h = 9,8 cm et r = 6,6 cm ÷ 2 = 3,3 cm ; d'où Vcylindre = π × 3,32 × 9,8 cm
 335 cm3.
335 cm3.Or, 1 L = 1 dm3 ; d'où 1 cL = 10 cm3. Donc : 335 cm3 = 33,5 cL.
Le volume de la canette est bien supérieur à 33 cL.
B. Hauteur minimum d'une canette « slim » de diamètre 5,6 cm pour qu'elle contienne au moins 33 cL
Soit h la hauteur cherchée.Ici, r = 5,6 cm ÷ 2 = 2,8 cm.
On sait que : Vcylindre = πr2h et on veut Vcylindre
 330 cm3 ; d'où : π × 2,82 × h
330 cm3 ; d'où : π × 2,82 × h  330 cm3.
330 cm3.Et donc : h

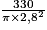 cm, soit : h
cm, soit : h  13,4 cm.
13,4 cm.La canette « slim » doit avoir une hauteur minimale de 13,4 cm pour contenir au moins 33 cL de boisson.
C. Lien entre rayon de la base et aire du patron d'une canette de 33 cL
1. Expression de h en fonction de r
Soit r le rayon et h la hauteur du cylindre. On a : Vcylindre = πr2h.
Si Vcylindre = 330 cm3 (= 33 cL), alors h =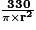 cm.
cm.
Soit r le rayon et h la hauteur du cylindre. On a : Vcylindre = πr2h.
Si Vcylindre = 330 cm3 (= 33 cL), alors h =
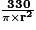 cm.
cm.2. Expression de L en fonction de r
La longueur L est égale au périmètre du disque de base du cylindre, d'où : L = 2πr.
La longueur L est égale au périmètre du disque de base du cylindre, d'où : L = 2πr.
3. Expression de l'aire du rectangle en fonction de r
Airerectangle = Longueur × largeur = L × h. Or h =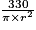 cm d'après la question C.1. et L = 2πr d'après la question C.2.
cm d'après la question C.1. et L = 2πr d'après la question C.2.
D'où :
Airerectangle =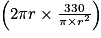 cm2 =
cm2 = 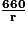 cm2.
cm2.
Airerectangle = Longueur × largeur = L × h. Or h =
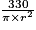 cm d'après la question C.1. et L = 2πr d'après la question C.2.
cm d'après la question C.1. et L = 2πr d'après la question C.2.D'où :
Airerectangle =
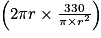 cm2 =
cm2 = 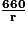 cm2.
cm2.4. Expression de l'aire totale en fonction de r
On a : Airecylindre = Airerectangle + 2 × Airedisque.
D'après la question précédente, l'aire du rectangle est :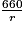 cm2.
cm2.
On a donc : Airecylindre =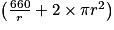 cm2.
cm2.
L'aire du cylindre, est, en cm2 :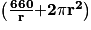 .
.
On a : Airecylindre = Airerectangle + 2 × Airedisque.
D'après la question précédente, l'aire du rectangle est :
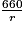 cm2.
cm2.On a donc : Airecylindre =
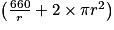 cm2.
cm2.L'aire du cylindre, est, en cm2 :
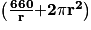 .
.D. Lectures graphiques
1. Aire de la surface de métal nécessaire pour un cylindre de base 1,5 cm
Sur le graphique, le point de la courbe qui a pour abscisse 1,5 a pour ordonnée 450.
On en déduit qu'un cylindre dont le rayon de base mesure 1,5 cm a une aire mesurant 450 cm2.
Sur le graphique, le point de la courbe qui a pour abscisse 1,5 a pour ordonnée 450.
On en déduit qu'un cylindre dont le rayon de base mesure 1,5 cm a une aire mesurant 450 cm2.
2. Valeur(s) du rayon correspondant à une aire de 300 cm2
Il y a deux points de la courbe d'ordonnée 300. L'un a pour abscisse 2,5 ; l'autre a pour abscisse 5,25.
On en déduit qu'une aire de 300 cm2 correspond à un cylindre de 2,5 cm ou de 5,25 cm de rayon.
Il y a deux points de la courbe d'ordonnée 300. L'un a pour abscisse 2,5 ; l'autre a pour abscisse 5,25.
On en déduit qu'une aire de 300 cm2 correspond à un cylindre de 2,5 cm ou de 5,25 cm de rayon.
3. Choix du modèle de canette utilisant le moins de métal
La canette classique a une contenance d'environ 33 cL et un rayon de 3,3 cm.
La canette slim a une contenance de 33 cL et un rayon de 2,8 cm.
Sur la courbe, on lit que le point d'abscisse 3,3 a une ordonnée inférieure à celle du point d'abscisse 2,8.
La canette classique a donc une surface de métal inférieure à celle de la canette slim.
La canette classique a une contenance d'environ 33 cL et un rayon de 3,3 cm.
La canette slim a une contenance de 33 cL et un rayon de 2,8 cm.
Sur la courbe, on lit que le point d'abscisse 3,3 a une ordonnée inférieure à celle du point d'abscisse 2,8.
La canette classique a donc une surface de métal inférieure à celle de la canette slim.
4. Valeur du rayon correspondant à la surface de métal minimale pour une canette de 33 cL
Le minimum de la courbe a une abscisse comprise entre 3,5 et 4, soit environ 3,75.
Le rayon correspondant à la surface de métal minimale est donc d'environ 3,75 cm.
Le minimum de la courbe a une abscisse comprise entre 3,5 et 4, soit environ 3,75.
Le rayon correspondant à la surface de métal minimale est donc d'environ 3,75 cm.
E. Utilisation d'un tableur
1. Formule à entrer dans la cellule B2
Il faut entrer la formule : =2*PI()*B1^2+660/B1.
Il faut entrer la formule : =2*PI()*B1^2+660/B1.
2. Encadrement du rayon du cylindre d'aire minimale
Le tableau permet de dire que le rayon de base du cylindre d'aire minimale est compris entre 3,6 cm et 3,8 cm.
Le tableau permet de dire que le rayon de base du cylindre d'aire minimale est compris entre 3,6 cm et 3,8 cm.
Remarque
En fait, le tableau seul ne permet pas de répondre en ce sens, les valeurs données étant discrètes. C'est l'observation croisée du tableau et de la courbe, laquelle ne fait pas apparaître d'« irrégularités » entre les valeurs discrètes du tableau, qui permet de répondre…3. Hauteur de la canette de rayon de base 3,7 cm
D'après la réponse à la question C.1., la hauteur d'une canette de contenance 33 cL est donnée en fonction du rayon de base par la formule : h =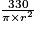 , avec r en cm.
, avec r en cm.
Donc, si r = 3,7 cm, alors h =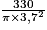 cm
cm  7,7 cm.
7,7 cm.
D'après la réponse à la question C.1., la hauteur d'une canette de contenance 33 cL est donnée en fonction du rayon de base par la formule : h =
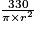 , avec r en cm.
, avec r en cm.Donc, si r = 3,7 cm, alors h =
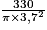 cm
cm  7,7 cm.
7,7 cm.F.
1. Masse d'aluminium nécessaire pour la fabrication d'une canette classique
Il faut 268,42 cm2, soit 0,026 842 m2 pour fabriquer le cylindre.
Comme la tôle d'aluminium a une épaisseur de 130 × 10−6 m, le volume d'aluminium utilisé pour le cylindre est, en m3 : 130 × 10−6 × 0,026 842 = 3,489 46 × 10−6.
La masse volumique de l'aluminium étant 2 700 kg/m3, la masse de tôle nécessaire à la fabrication du cylindre est, en kg : 2 700 × 3,489 46 × 10−6 0,009 42, soit environ 9,42 g.
0,009 42, soit environ 9,42 g.
Ce à quoi il faut ajouter la masse de l'anneau, 1,4 g, et celle des soudures, soit 1,9 g.
9,42 + 1,4 + 1,9 = 12,72
Il faut environ 12,7 g d'aluminium pour réaliser une canette classique.
Il faut 268,42 cm2, soit 0,026 842 m2 pour fabriquer le cylindre.
Comme la tôle d'aluminium a une épaisseur de 130 × 10−6 m, le volume d'aluminium utilisé pour le cylindre est, en m3 : 130 × 10−6 × 0,026 842 = 3,489 46 × 10−6.
La masse volumique de l'aluminium étant 2 700 kg/m3, la masse de tôle nécessaire à la fabrication du cylindre est, en kg : 2 700 × 3,489 46 × 10−6
 0,009 42, soit environ 9,42 g.
0,009 42, soit environ 9,42 g.Ce à quoi il faut ajouter la masse de l'anneau, 1,4 g, et celle des soudures, soit 1,9 g.
9,42 + 1,4 + 1,9 = 12,72
Il faut environ 12,7 g d'aluminium pour réaliser une canette classique.
Remarque
La question de savoir s'il faut ajouter deux fois la masse des soudures est discutable. Effectivement, le sujet parle du « couvercle » et laisse sous silence la question du « fond » de la canette.2. Nombre de canettes nécessaires pour la fabrication d'un vélo
Le vélo pèse 9 kg, soit 9 000 g.
9 000 ÷ 12,7 708,66.
708,66.
Il faut environ 709 canettes pour fabriquer le vélo.
Le vélo pèse 9 kg, soit 9 000 g.
9 000 ÷ 12,7
 708,66.
708,66.Il faut environ 709 canettes pour fabriquer le vélo.
Deuxième partie
Exercice 1
1. Probabilité qu'une personne choisie au hasard soit « donneur universel »
D'après le tableau 2, les donneurs universels sont les personnes de groupe O, rhésus négatif. D'après le tableau 1, ces personnes représentent 6 % de la population française.
La probabilité qu'une personne choisie au hasard soit « donneur universel » est donc 6 %.
D'après le tableau 2, les donneurs universels sont les personnes de groupe O, rhésus négatif. D'après le tableau 1, ces personnes représentent 6 % de la population française.
La probabilité qu'une personne choisie au hasard soit « donneur universel » est donc 6 %.
2. Probabilité qu'une personne choisie au hasard soit « receveur universel »
D'après le tableau 2, les receveurs universels sont les personnes de groupe AB, rhésus positif. D'après le tableau 1, ces personnes représentent 3 % de la population.
La probabilité qu'une personne choisie au hasard soit « receveur universel » est : 3 %.
D'après le tableau 2, les receveurs universels sont les personnes de groupe AB, rhésus positif. D'après le tableau 1, ces personnes représentent 3 % de la population.
La probabilité qu'une personne choisie au hasard soit « receveur universel » est : 3 %.
3. Probabilité qu'une personne choisie au hasard puisse donner son sang à une personne du groupe B, rhésus +
D'après le tableau 2, les personnes pouvant donner leur sang à une personne du groupe B, rhésus +, sont les personnes des groupes O et B (rhésus positif et négatif).
Ces personnes représentent respectivement 36 %, 6 %, 9 % et 1 % de la population.
On a : 36 + 6 + 9 + 1 = 52.
La probabilité qu'une personne choisie au hasard puisse donner son sang à une personne du groupe B, rhésus +, est donc : 52 %.
D'après le tableau 2, les personnes pouvant donner leur sang à une personne du groupe B, rhésus +, sont les personnes des groupes O et B (rhésus positif et négatif).
Ces personnes représentent respectivement 36 %, 6 %, 9 % et 1 % de la population.
On a : 36 + 6 + 9 + 1 = 52.
La probabilité qu'une personne choisie au hasard puisse donner son sang à une personne du groupe B, rhésus +, est donc : 52 %.
4. Probabilité qu'une personne choisie au hasard parmi les personnes du groupe O soit « donneur universel »
Les donneurs universels représentent 6 % de la population française. Les personnes du groupe O représentent 42 % de la population française (36 % pour les O+ et 6 % pour les O−).
On a :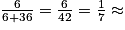 0,143.
0,143.
La probabilité qu'une personne choisie au hasard parmi les personnes du groupe O soit « donneur universel » est d'environ 14 %.
Les donneurs universels représentent 6 % de la population française. Les personnes du groupe O représentent 42 % de la population française (36 % pour les O+ et 6 % pour les O−).
On a :
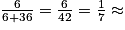 0,143.
0,143.La probabilité qu'une personne choisie au hasard parmi les personnes du groupe O soit « donneur universel » est d'environ 14 %.
5. Nombre de « donneurs universels » en France au 1er janvier 2016
Remarque
Il y a une ambiguïté ici : les donneurs universels sont-ils, comme pour les questions précédentes, à considérer dans l'ensemble de la population française, ou parmi les donneurs de sang ?Nous considérons que, comme pour les questions précédentes, les donneurs universels (potentiels) sont à prendre en compte dans l'ensemble de la population française.
D'après la question 1., il y a 6 % de donneurs universels parmi les 66 627 602 Français.
On a :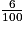 × 66 627 602 = 3 997 656,12.
× 66 627 602 = 3 997 656,12.
Au 1er janvier 2016, il y avait environ 4 millions de donneurs universels en France.
D'après la question 1., il y a 6 % de donneurs universels parmi les 66 627 602 Français.
On a :
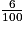 × 66 627 602 = 3 997 656,12.
× 66 627 602 = 3 997 656,12.Au 1er janvier 2016, il y avait environ 4 millions de donneurs universels en France.
6. Pourcentage de la population française susceptible de donner son sang
43 217 325 personnes, parmi les 66 627 602 Français, sont susceptibles de donner leur sang.
On a :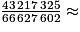 0,65.
0,65.
Environ 65 % de la population française est susceptible de donner son sang.
43 217 325 personnes, parmi les 66 627 602 Français, sont susceptibles de donner leur sang.
On a :
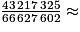 0,65.
0,65.Environ 65 % de la population française est susceptible de donner son sang.
Exercice 2
On avance d'une case grâce à la commande « avancer de 60 » ; il faut donc commander « avancer de 180 » pour avancer de trois cases.La commande « tourner de 270 degrés dans le sens horaire » permet de tourner à gauche. Pour tourner à droite, il faut « tourner de 90 degrés dans le sens horaire ».
Les nombres « 120 », « 270 » et « 60 » doivent être remplacés par : « 180 », « 90 » et « 60 » pour programmer le déplacement du lutin de la case « Nantes » à la case « Lyon ».
Exercice 3
1. Calcul mental de 452
45 est composé de 4 dizaines et de 5 unités. On calcule : 4 × 5 = 20, ce qui donne le nombre de centaines du résultat, et on écrit 25 à droite de 20 pour obtenir le résultat.
On obtient : 452 = 2 025.
45 est composé de 4 dizaines et de 5 unités. On calcule : 4 × 5 = 20, ce qui donne le nombre de centaines du résultat, et on écrit 25 à droite de 20 pour obtenir le résultat.
On obtient : 452 = 2 025.
2. Égalité n2 = 100d(d + 1) + 25
Soit n un nombre entier s'écrivant 10d + 5. On a :
n2 = (10d + 5)2 = (10d)2 + 2 × 5 × 10d + 52 = 100d2 + 100d + 25 = 100d(d + 1) + 25.
Soit n un nombre entier s'écrivant 10d + 5. On a :
n2 = (10d + 5)2 = (10d)2 + 2 × 5 × 10d + 52 = 100d2 + 100d + 25 = 100d(d + 1) + 25.
3. Lien entre égalité algébrique et méthode de calcul mental
L'égalité qui précède permet de dire que (10d + 5)2 est égal à d(d + 1) centaines, plus 25.
Or d(d + 1) correspond au produit du nombre de dizaines de 10d + 5 par le nombre suivant.
On retrouve donc la technique de calcul mental évoquée dans l'énoncé.
L'égalité qui précède permet de dire que (10d + 5)2 est égal à d(d + 1) centaines, plus 25.
Or d(d + 1) correspond au produit du nombre de dizaines de 10d + 5 par le nombre suivant.
On retrouve donc la technique de calcul mental évoquée dans l'énoncé.
4. Extension au calcul mental de 3,52
On observe que 3,5 = 35 × 0,1 et donc que : 3,52 = (35 × 0,1)2 = 352 × 0,01.
On applique la technique de calcul mental à 352 pour obtenir : 352 = 1 225 (soit 3 × 4 × 100 + 25), puis on divise le résultat par 100 (ce qui correspond à multiplier par 0,01).
On obtient : 3,52 = 12,25.
On observe que 3,5 = 35 × 0,1 et donc que : 3,52 = (35 × 0,1)2 = 352 × 0,01.
On applique la technique de calcul mental à 352 pour obtenir : 352 = 1 225 (soit 3 × 4 × 100 + 25), puis on divise le résultat par 100 (ce qui correspond à multiplier par 0,01).
On obtient : 3,52 = 12,25.
Exercice 4
1. Figure
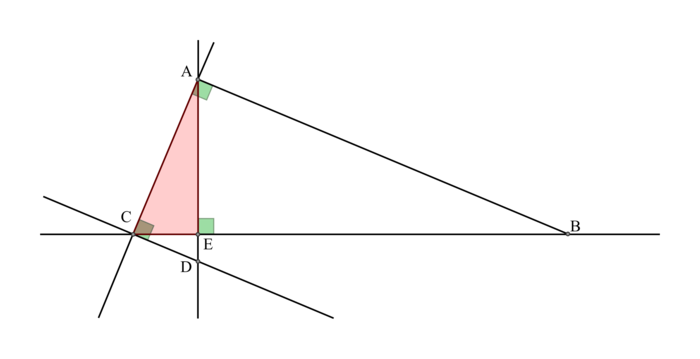 Cette figure est à l'échelle, mais pas à la taille demandée. |
2. Calcul de l'aire du triangle CEA
Remarque
On observe que la seule donnée de la longueur AE dans le triangle AEC ne permet pas de calculer immédiatement l'aire du triangle AEC.Dans le triangle rectangle ABE, deux des longueurs de côtés sont connues, ce qui permet de calculer la longueur du troisième côté (grâce au théorème de Pythagore et/ou les mesures des angles à l'aide des formules de trigonométrie).
Le triangle AEB est rectangle en E, donc  et
et  sont complémentaires.
sont complémentaires.
Par ailleurs, C est sur la perpendiculaire à (AB) passant par A, donc l'angle est droit. On en déduit que les angles
est droit. On en déduit que les angles  et
et  sont aussi complémentaires et donc que
sont aussi complémentaires et donc que  et
et  sont égaux.
sont égaux.
Les triangles AEC et AEB sont tous deux rectangles en E et ont un deuxième angle égal, ils sont donc semblables.
Deux triangles semblables ont des longueurs proportionnelles.
Le côté AE, dans le triangle AEC, correspond au côté EB, dans le triangle ABE. Le rapport de réduction pour passer des longueurs des côtés de AEB à celles de AEC est donc : k =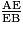 .
.
On a alors : AireAEC = k2 × AireAEB (1).
Dans le triangle AEB, rectangle en E, d'après le théorème de Pythagore, on a :
AB2 = AE2 + EB2, d'où : EB2 = AB2 − AE2. Or : AB = 13 cm et AE = 5 cm. On en déduit :
EB =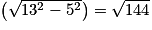 = 12 cm.
= 12 cm.
Par conséquent : k =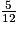 et AireAEB =
et AireAEB = 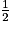 × AE × EB = (0,5 × 5 × 12) cm2 = 30 cm2.
× AE × EB = (0,5 × 5 × 12) cm2 = 30 cm2.
On remplace dans (1) et on obtient :
AireAEC =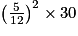 cm2
cm2  5,2083 cm2
5,2083 cm2  520,8 mm2.
520,8 mm2.
L'aire du triangle AEC mesure environ 520,8 mm2.
 et
et  sont complémentaires.
sont complémentaires.Par ailleurs, C est sur la perpendiculaire à (AB) passant par A, donc l'angle
 est droit. On en déduit que les angles
est droit. On en déduit que les angles  et
et  sont aussi complémentaires et donc que
sont aussi complémentaires et donc que  et
et  sont égaux.
sont égaux.Les triangles AEC et AEB sont tous deux rectangles en E et ont un deuxième angle égal, ils sont donc semblables.
Deux triangles semblables ont des longueurs proportionnelles.
Le côté AE, dans le triangle AEC, correspond au côté EB, dans le triangle ABE. Le rapport de réduction pour passer des longueurs des côtés de AEB à celles de AEC est donc : k =
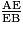 .
.On a alors : AireAEC = k2 × AireAEB (1).
Dans le triangle AEB, rectangle en E, d'après le théorème de Pythagore, on a :
AB2 = AE2 + EB2, d'où : EB2 = AB2 − AE2. Or : AB = 13 cm et AE = 5 cm. On en déduit :
EB =
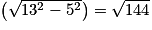 = 12 cm.
= 12 cm.Par conséquent : k =
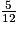 et AireAEB =
et AireAEB = 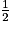 × AE × EB = (0,5 × 5 × 12) cm2 = 30 cm2.
× AE × EB = (0,5 × 5 × 12) cm2 = 30 cm2.On remplace dans (1) et on obtient :
AireAEC =
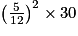 cm2
cm2  5,2083 cm2
5,2083 cm2  520,8 mm2.
520,8 mm2.L'aire du triangle AEC mesure environ 520,8 mm2.
Troisième partie
Situation 1
1. Deux procédures de dénombrement d'une collection de trois objets, en petite section
Un élève de petite section peut dénombrer une collection de trois objets par subitizing (reconnaissance perceptive globale).
Il peut également recomposer trois en reconnaissant deux et un, et en s'appuyant sur sa connaissance que « deux et un, ça fait trois ».
Un élève de petite section peut dénombrer une collection de trois objets par subitizing (reconnaissance perceptive globale).
Il peut également recomposer trois en reconnaissant deux et un, et en s'appuyant sur sa connaissance que « deux et un, ça fait trois ».
Remarque
On pourrait, bien sûr, évoquer ici le comptage, mais cette procédure est déconseillée en petite section, sur des quantités inférieures à quatre car :1) elle est coûteuse et non nécessaire, le subitizing étant possible jusqu'à trois inclus ;
2) l'apprentissage trop précoce du comptage se fait souvent au détriment de la construction du sens des concepts de collection et de quantité.
2. Exemple d'activité en moyenne section pour travailler les décompositions du nombre quatre
Pour travailler les décompositions du nombre quatre, on peut proposer à des élèves de moyenne section de « décorer » les deux ailes d'une coccinelle avec des points, de telle sorte que la coccinelle ait exactement quatre points en tout.
L'observation des différentes productions des élèves, ainsi que la verbalisation qui l'accompagnera (par exemple : « il y a un point d'un côté et trois points de l'autre côté »), permettra de prendre conscience des différentes décompositions de quatre.
Pour travailler les décompositions du nombre quatre, on peut proposer à des élèves de moyenne section de « décorer » les deux ailes d'une coccinelle avec des points, de telle sorte que la coccinelle ait exactement quatre points en tout.
L'observation des différentes productions des élèves, ainsi que la verbalisation qui l'accompagnera (par exemple : « il y a un point d'un côté et trois points de l'autre côté »), permettra de prendre conscience des différentes décompositions de quatre.
3. Intérêt à utiliser le dé proposé, en grande section
Un enseignant de grande section peut utiliser le type de dé proposé dans le but d'entraîner les élèves à reconnaître des constellations autres que celles usuelles. Celles proposées présentent par ailleurs l'avantage de permettre une discrimination immédiate des nombres pairs et des nombres impairs, ce qui, en parallèle d'un début de travail sur les doubles et les moitiés, peut s'avérer intéressant.
Un enseignant de grande section peut utiliser le type de dé proposé dans le but d'entraîner les élèves à reconnaître des constellations autres que celles usuelles. Celles proposées présentent par ailleurs l'avantage de permettre une discrimination immédiate des nombres pairs et des nombres impairs, ce qui, en parallèle d'un début de travail sur les doubles et les moitiés, peut s'avérer intéressant.
Situation 2
1. Analyse de production d'élèves (procédures et erreurs éventuelles)
• Robin sait que 5 est la moitié de 10. Il calcule en ligne le produit de 68 par 10, puis divise le résultat obtenu par 2 (peut-être chiffre par chiffre).
Il n'y a pas d'erreur de calcul, tout au plus une erreur d'écriture (10 × 68 = 680 ÷ 2), mais sans conséquence sur le résultat.
Il n'y a pas d'erreur de calcul, tout au plus une erreur d'écriture (10 × 68 = 680 ÷ 2), mais sans conséquence sur le résultat.
Remarque
Les documents d'accompagnement des programmes soulignent le fait que ce type d'erreur d'écriture est, d'une part, usuel et, d'autre part, présente l'avantage d'expliciter les étapes de calcul. Les égalités sont bien sûr mathématiquement fausses et doivent petit à petit être remplacées, mais avec souplesse et tolérance de la part de l'enseignant• Eléonore sait que 68 = 70 − 2. Elle calcule en ligne 70 × 5, puis 2 × 5 et soustrait le deuxième produit au premier, mobilisant implicitement la distributivité de la multiplication sur la soustraction.
Il n'y a pas d'erreur.
Il n'y a pas d'erreur.
• Lucie décompose mentalement 68 en 60 plus 8. Elle effectue en ligne le produit de 60 par 5, puis celui de 8 par 5 et additionne, en ligne toujours, les produits obtenus.
Il n'y a pas d'erreur.
Il n'y a pas d'erreur.
• Mathys décompose chiffre par chiffre le nombre 68, sans tenir compte des unités de numération, ce qui est une erreur. Il effectue en ligne, sans faute, les produits 5 × 6 et 5 × 8, puis additionne les résultats obtenus. Il n'y a pas d'erreur de calcul à ce stade.
Le résultat est, bien sûr, erroné.
Le résultat est, bien sûr, erroné.
2. Trois démarches pour calculer en ligne 25 × 28 au cycle 3 et connaissances en jeu
• Première démarche
| 25 × 28 | = (100 ÷ 4) × 28 | Connaissance du fait numérique : 25 est le quart de 100 |
| = (28 × 100) ÷ 4 | Connaissance (en actes) de la commutativité de la multiplication | |
| = 2 800 ÷ 4 | Connaissance du système de numération : effet du produit par 100 sur les unités de numération (les unités « deviennent » des centaines) et transcription en écriture décimale de 28 centaines | |
| = 700 | (Re)connaissance de 28 comme étant égal à 4 × 7 et connaissance du système de numération (pour dire que 2 800, c'est 28 centaines, puis que 7 centaines s'écrit : 700) |
• Deuxième démarche
| 25 × 28 | = 25 × (30 − 2) | Connaissance du complément de 28 à la dizaine et de la dizaine supérieure |
| = (25 × 30) − (25 × 2) | Connaissance (en actes) de la distributivité de la multiplication sur la soustraction | |
| = (25 × 3) × 10 − 50 | Connaissance de la décomposition multiplicative : 30 = 3 × 10 et du double de 25, associativité de la multiplication | |
| = 75 × 10 − 50 | Connaissance du triple de 25 | |
| = 750 − 50 | Connaissance du système de numération : effet du produit par 10 sur les unités de numération (les unités « deviennent » des dizaines) et transcription en écriture décimale de 75 dizaines | |
| = 700 + 50 − 50 | Connaissance de la décomposition 750 = 700 + 50 et de la réversibilité de l'ajout et du retrait d'un même nombre | |
| = 700 |
• Troisième démarche
| 25 × 28 | = (20 + 5) × (20 + 8) | Connaissance des décompositions en dizaines et unités |
| = 20 × 20 + 20 × 8 + 5 × 20 + 5 × 8 | Connaissance (en actes) de la distributivité de la multiplication sur l'addition | |
| = 400 + 160 + 100 + 40 | Connaissance de faits numériques (tables de 2 et de 5), multiples de 10 ; associativité et commutativité de la multiplication (en actes) | |
| = (400 + 100) + (160 + 40) | Commutativité et associativité de l'addition (en actes) | |
| = 500 + 200 | Connaissance des tables d'addition et des décompositions en unités de numération | |
| = 700 |
Remarque
Le fait qu'il s'agisse ici de connaissances ou de compétences pourrait être discuté. Nous avons formulé les réponses en termes de connaissances, pour nous conformer à la demande.Situation 3
1. Champ mathématique travaillé
Cette situation permet de travailler le concept de proportionnalité, plus précisément d'agrandissement.
Cette situation permet de travailler le concept de proportionnalité, plus précisément d'agrandissement.
2. Analyse des productions 1 à 3 (stratégies, réussites, erreurs)
• Groupe 1
- Stratégie : reprise sous forme de dessin des données fournies (pièces constitutives du puzzle, nom des pièces et dimensions) ; ajout de 2 cm à toutes les longueurs des trois segments constitutifs de chacun de deux des côtés adjacents du carré et ajout de 3 cm à chacune des longueurs des deux segments constitutifs des deux côtés restant du carré. Les élèves ont sûrement observé que 3 × 2 = 2 × 3…
- Réussite : le contour carré reste carré.
- Erreur : les pièces constitutives du puzzle ne sont pas agrandies de façon proportionnelle.
• Groupe 2
- Stratégie : les élèves énoncent un principe calculatoire : chaque mesure de longueur doit se voir ajouter son quart, multiplié par deux. Les correspondances entre données initiales et dimensions à produire sont ensuite notées à l'aide de flèches.
- Réussites : le lien multiplicatif entre 4 et 6 est correct. Le concept d'agrandissement est compris. Les dimensions trouvées sont correctes.
- Erreur : il s'agit plus d'une maladresse… les élèves n'ont pas perçu le rapport multiplicatif 1,5 comme étant « un plus la moitié » mais comme « un plus le double du quart », ce qui complique les calculs et augmente donc les risques d'erreur. Cela dit, les calculs sont corrects.
• Groupe 3
- Stratégie : les élèves observent que, pour passer de 4 à 6, on divise par deux, puis on multiplie le résultat par trois. Ils appliquent ces opérations à toutes les données numériques, en présentant la correspondance entre données initiales et données cherchées par des flèches, accompagnées de l'écriture des calculs correspondants en ligne.
- Réussite : les calculs sont justes ; le concept d'agrandissement est compris ; le lien multiplicatif entre les données est correct.
3. Procédures utilisées par le groupe 4
- La correspondance entre 4 et 6 est reprise explicitement de l'énoncé.
- Pour passer de 6 à 9, les élèves semblent avoir observé que 6 est égal à 4 plus la moitié de 4 (données initiales) ; ils ajoutent donc à 6 la moitié de 6.
- Il n'y a pas d'explication pour le passage de 7 à 10,5, peut-être parce que les élèves ont procédé de la même manière (7 plus la moitié de 7) ?
- Pour la correspondance de 2 et 3, les élèves ont observé que 2 est la moitié de 4 (donnée initiale) ; son correspondant est donc la moitié du correspondant de 4, soit la moitié de 6.
- Pour la correspondance de 5 et 7,5, les élèves ont observé que 5 est égal à 4 plus la moitié de 2. Ils font donc correspondre à 5 le correspondant de 4 (soit 6) plus la moitié du correspondant de 2 précédemment calculé (soit 3) et obtiennent : 6 + (3 ÷ 2) = 7,5.
- Ils procèdent de façon similaire pour 9, en observant que 9 = 4 + 4 + 1. Ils font donc correspondre à 9 : 6 + 6 + (3 ÷ 2) = 13,5.
