Dernier essai le
- Score :
/20
Fonction affine
On appelle fonction (ou application) affine f une relation qui, à chaque nombre x, associe le nombre ax + b, a et b étant deux nombres connus. On dit que ax + b est l'image de x par cette fonction affine.
Exemple
Considérons la fonction affine f définie par : f(x) = –2x + 5. Pour connaître l'image d'un nombre par f, on multiplie ce nombre par –2 et on ajoute 5 au résultat.
La représentation graphique de la fonction f est la droite d'équation y = –2x + 5.
La représentation graphique de la fonction f est la droite d'équation y = –2x + 5.
Fonction constante
Une fonction (ou application) constante est une fonction affine de la forme : f(x) = b.
Exemple
La fonction f(x) = –3 est une fonction constante.
À chaque nombre x, elle associe le nombre –3. Sa représentation graphique est la droite d'équation y = –3.
Cette droite est parallèle à l'axe des abscisses et passe par le point (0 ; –3).
À chaque nombre x, elle associe le nombre –3. Sa représentation graphique est la droite d'équation y = –3.
Cette droite est parallèle à l'axe des abscisses et passe par le point (0 ; –3).
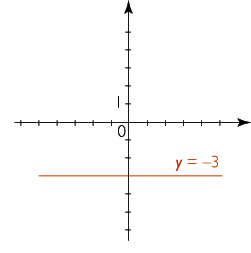 |
Fonction linéaire
On appelle fonction (ou application) linéaire une relation qui, à chaque nombre x, associe le nombre ax, a étant un nombre connu. On dit que ax est l'image de x par cette fonction linéaire.
Une fonction linéaire est donc une fonction affine particulière.
Une fonction linéaire est donc une fonction affine particulière.
Exemple
Considérons la fonction linéaire f définie par f(x) = 4x.
Pour connaître l'image d'un nombre par f, on multiplie ce nombre par 4.
La représentation graphique de la fonction f est la droite d'équation y = 4x. Elle passe par l' origine du repère.
Pour connaître l'image d'un nombre par f, on multiplie ce nombre par 4.
La représentation graphique de la fonction f est la droite d'équation y = 4x. Elle passe par l' origine du repère.
Document précédent
Les multiples
