Enseignement Les épreuves du CRPE
Les calculs avec puissances et racines carrées
Imprimer
Dernier essai le - Score : /20
Propriétés des puissances
Propriété
a et b désignent des nombres relatifs (a    0), n et p des nombres entiers relatifs. Les propriétés ci-dessous définissent :
  • le produit de deux puissances de même exposant : a n   ×   b n  = (ab) n  ;
  • le produit de deux puissances du même nombre : a n   ×   a p  =  a n +p      ;
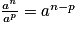  • le quotient de deux puissances du même nombre : \frac{a^n}{a^p} = a^{n-p}  ;
  • une puissance de puissance  : (a n ) p  =  a np .
Exemple
Produit de deux puissances de même exposant : A  = (–7)3   ×  53  = (–7  ×  5)3  = (–35)3.
Produit de deux puissances du même nombre : B  =  4 3 ×   4 −9 = 43 + (−9) = 43 − 9 = 4−6
Propriétés des racines carrées
Propriété
Pour tous nombres positifs a et b, on a les égalités suivantes :
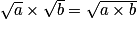\sqrt{a}\times\sqrt{b} = \sqrt{a\times b}  ;
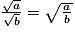\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b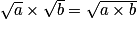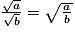}}, avec b   0.
Exemple
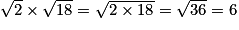
\sqrt{2}\times\sqrt{18} = \sqrt{2\times 18} = \sqrt{36} = 6
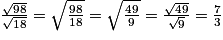
\frac{\sqrt{98}}{\sqrt{18}} = \sqrt{\frac{98}{18}} = \sqrt{\frac{49}{9}} = \frac{\sqrt{49}}{\sqrt{9}} = \frac{7}{3}
Ces exemples montrent que le produit ou le quotient de deux nombres irrationnels peut être un nombre rationnel.