Enseignement Les épreuves du CRPE
Les aires
Imprimer
Dernier essai le - Score : /20
Aire
Donner l'aire d'une surface, c'est indiquer sa grandeur, son étendue.
Une aire s'exprime par un nombre suivi d'une unité d'aire.
Exemple
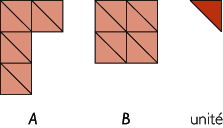
Prenons pour unité d'aire le triangle rouge ci-dessous.
Pour recouvrir la surface A, on a besoin de 8 triangles unités.
Pour recouvrir la surface B, on a besoin également de 8 triangles unités.
Dans l'unité choisie, l'aire des deux figures A et B est donc 8.
Remarque
Les unités d'aire du système métrique sont le mètre carré (m2), ses multiples et ses sous-multiples.
Pour passer de l'une à l'autre, il faut multiplier par 100 pour obtenir l'unité immédiatement supérieure et diviser par 100 pour obtenir l'unité immédiatement inférieure.
Aire d'un cylindre
L'aire d'un cylindre de révolution est égale à la somme des aires de ses deux disques de base et de sa surface latérale.
Exemple
Soit un cylindre de hauteur h et de rayon de base r.
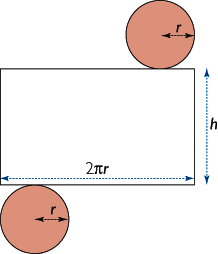Son aire latérale est celle d'un rectangle ayant pour dimensions le périmètre du disque de base 2 ×  π  ×  r et la hauteur h du cylindre, soit 2π r  ×  h. L'aire d'un disque de base est égale à π r 2. L'aire A du cylindre de révolution est donc égale à : 2π r  ×  h  + 2 ×  π r 2.
Aire d'un disque
Soit r le rayon d'un disque, l'aire   A de ce disque est donnée par la formule   A  =  π  ×  r  ×  r  =  π r 2 (une valeur approchée du nombre  π est 3,14).
Exemple
Un disque dont le rayon mesure 4 cm a une aire égale, en cm2, à π  × 4 × 4, soit environ 50,24.
Aire d'un parallélépipède rectangle
Soit L, l et h les trois dimensions d'un parallélépipède rectangle (ou pavé droit), l'aire totale  A de ce solide (celle de ses six faces) est donnée par la formule :
A  = 2 × (L  ×  l  +  L  ×  h  +  l  ×  h) ou A  = 2Ll  + 2Lh  + 2lh.
Exemple
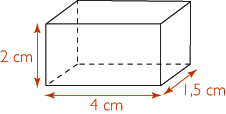L'aire du pavé droit représenté ci-dessus est égale à 34 cm2.
En effet : 2 × (4 × 1,5 + 4 × 2 + 1,5 × 2) = 34.
Aire d'un parallélogramme
Soit c la longueur d'un côté d'un parallélogramme et h celle de la hauteur associée à ce côté, l'aire   A de ce parallélogramme est donnée par la formule   A  =  c  ×  h (c et h doivent être exprimées dans la même unité).
Exemple
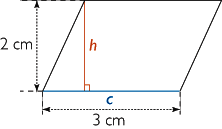L'aire du parallélogramme représenté ci-dessus est égale à 6 cm2 (car 3 × 2 = 6).
Aire d'un triangle
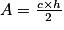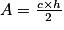Soit c la longueur d'un côté d'un triangle et h celle de la hauteur associée à ce côté, l'aire   A de ce triangle est donnée par la formule   A = \frac{c\times h}{2} (c et h doivent être exprimées dans la même unité).
Exemple
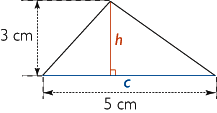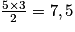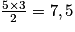Le triangle représenté ci-dessus a une aire égale, en cm2, à  \frac{5\times 3}{2}=7,5.
Aire d'une sphère
L'aire A d'une sphère de rayon r est donnée par la formule A  = 4π r 2 (une valeur approchée du nombre π est 3,14).
Exemple
Cherchons l'aire d'une balle de tennis de table, sachant qu'elle a la forme d'une sphère de 38 mm de rayon.
Comme 4π  × 382 = 5 776  π, on trouve que l'aire de la balle est égale à 5 776  π  mm2, soit environ à 181 cm2.