Dernier essai le
- Score :
/20
Sujet
Sujet
Exercice 1 (4 points)
En empilant dix cubes identiques comme ci-dessous, on construit un escalier de hauteur : h = 4.
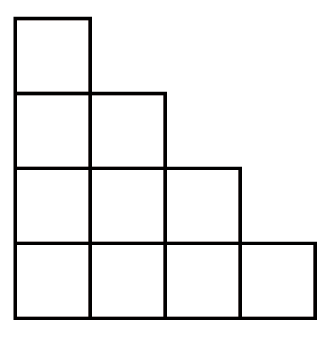 |
1) Indiquer le nombre de cubes nécessaires pour réaliser respectivement des escaliers de hauteur 5 et de hauteur 9.
2) Y a-t-il proportionnalité entre la hauteur des escaliers et le nombre de cubes nécessaires pour les construire ? Justifier votre réponse.
3) Avec deux escaliers identiques on peut construire un « mur ».
 |
À partir de l'observation de cette construction, déduire la formule qui donne le nombre de cubes nécessaires à la réalisation d'un escalier de hauteur h.
4) Calculer la hauteur de l'escalier le plus haut que l'on peut construire avec 3 523 cubes. Combien de cubes seront inutilisés ? Justifier votre réponse.
Exercice 2 (4 points)
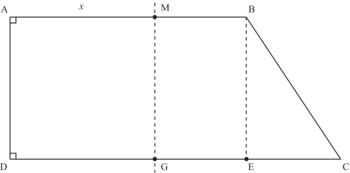
Le jardin de monsieur Durand a la forme d'un trapèze rectangle, ABCD, tel que AB = 50 m, AD = 30 m, DC = 70 m. Les angles  et
et  sont droits.
sont droits.
Soit M un point du segment [AB]. On pose AM = x.
La parallèle à la droite (AD) passant par M coupe la droite (DC) en G. Le jardin est ainsi partagé en deux parties :
 et
et 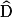 sont droits.
sont droits.Soit M un point du segment [AB]. On pose AM = x.
La parallèle à la droite (AD) passant par M coupe la droite (DC) en G. Le jardin est ainsi partagé en deux parties :
- le rectangle AMGD qui est le potager ;
- le reste qui est la pelouse.
1) Calculer l'aire du jardin.
2) Exprimer en fonction de x, l'aire du rectangle AMGD (le potager). En déduire l'aire de la pelouse BCGM.
3) Pour quelle valeur de x la pelouse et le potager ont-ils la même aire ? Quelle est alors la forme du potager. Justifier les réponses.
4) a. Représenter sur un même graphique, les fonctions donnant l'aire du potager AMGD et l'aire de la pelouse BCGM en fonction de x. On utilisera pour cela la feuille de papier millimétré et on prendra comme unités graphiques : 1 cm pour 10 mètres sur l'axe des abscisses, 1 cm pour 100 m2 sur l'axe des ordonnées.
La feuille de papier millimétré est à rendre avec la copie.
La feuille de papier millimétré est à rendre avec la copie.
b. Retrouver graphiquement le résultat de la question 3. Expliquer.
5) Sachant que dix kilos de semences sont nécessaires pour une pelouse de 500 m2, quelle quantité est nécessaire pour ensemencer 900 m2 ?
Question complémentaire (4 points)
En annexe 1, vous trouverez un problème tiré du manuel Cap math de CM2 ainsi que les productions de quatre élèves : Florent, Victor, Jessy et Cécile.
a. Décrire les procédures employées par chaque élève et préciser les propriétés mathématiques utilisées implicitement par les élèves.
b. Analyser les erreurs en émettant des hypothèses sur leur origine.
Exercice 3 (4 points)
Voici un jeu tiré de « Géométrie à l'école » de François Boule, Savoir dire et savoir-faire, IREM de Bourgogne. Il est constitué des dix étiquettes suivantes :
 |
On choisit au hasard deux étiquettes parmi les dix et on essaie de dessiner un quadrilatère qui a ces deux propriétés.
1) Avec un tel dispositif, combien de tirages différents est-il possible de réaliser ? Justifier votre réponse.
2) Un enfant a sélectionné les deux étiquettes suivantes :
 |
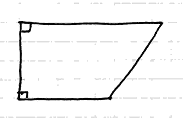
a. En se limitant à la première propriété « deux angles droits seulement », tracer à main levée les deux configurations possibles.
b. En prenant en compte les deux propriétés, construire à l'aide des outils usuels de géométrie (règle, équerre, compas) une figure correspondant à chacune des deux configurations possibles. Rédiger leur programme de construction.
3) On choisit l'étiquette :
 |
Trouver toutes les étiquettes incompatibles avec elle. Justifier les réponses.
4) On s'intéresse aux quadrilatères qui possèdent les deux propriétés :
 |
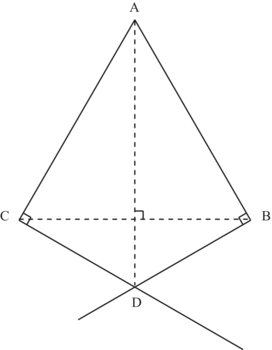
Soit ABCD un tel quadrilatère, on appelle E, F, G, H les milieux respectifs des côtés [AB], [BC], [CD] et [DA].
Quelle est la nature du quadrilatère EFGH ? Justifier.
Quelle est la nature du quadrilatère EFGH ? Justifier.
Question complémentaire (4 points)
a. Dans quel cycle de l'école primaire l'activité pédagogique décrite dans l'exercice 3 peut-elle être proposée ? Justifier la réponse.
b. Donner au moins deux objectifs que peut viser un enseignant qui propose ce jeu à ses élèves.
c. Trois élèves A, B et C ont tiré les deux étiquettes suivantes :
 |
Leurs travaux sont reproduits en annexe 2.
Décrire les procédures et relever les erreurs éventuelles de chaque production donnée en annexe 2.
Annexes
Annexe 1
 |
 |
 |
 |
 |
Annexe 2
 |
Corrigé
Corrigé
Exercice 1 (4 points)
1) Pour un escalier d'une hauteur de 5 cubes, il faut ajouter 5 cubes aux 10 cubes présents.
10 + 5 = 15.
Pour un escalier d'une hauteur de 6 cubes, on ajoutera 6 cubes aux 15 cubes présents.
10 + 5 + 6 = 21.
Pour un escalier d'une hauteur de 9 cubes, on ajoutera 9 cubes aux cubes présents.
10 + 5 + 6 + 7 + 8 + 9 = 45.
Un escalier d'une hauteur de 9 cubes sera constitué de 45 cubes.
10 + 5 = 15.
Pour un escalier d'une hauteur de 6 cubes, on ajoutera 6 cubes aux 15 cubes présents.
10 + 5 + 6 = 21.
Pour un escalier d'une hauteur de 9 cubes, on ajoutera 9 cubes aux cubes présents.
10 + 5 + 6 + 7 + 8 + 9 = 45.
Un escalier d'une hauteur de 9 cubes sera constitué de 45 cubes.
2) Pour qu'il y ait proportionnalité entre la hauteur de l'escalier h et le nombre de cubes c, il faudrait trouver un coefficient de proportionnalité k, tel que kc = h, soit k = 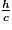 .
.
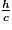 .
.Essayons avec les trois propositions de la question précédente :
Pour h = 5, k =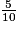 = 0,5.
= 0,5.
Pour h = 6, k =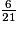 = 0,28.
= 0,28.
Pour h = 9, k =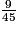 = 0,2.
= 0,2.
Pour h = 5, k =
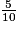 = 0,5.
= 0,5.Pour h = 6, k =
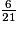 = 0,28.
= 0,28.Pour h = 9, k =
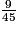 = 0,2.
= 0,2.Sur trois exemples, on ne peut dégager une constante, la hauteur de l'escalier n'est pas proportionnelle au nombre de cubes qui le constituent.
3) Pour le mur présenté en exemple, le nombre de cubes est égal à 4 × 5, soit 20 cubes. Le nombre de cubes pour l'escalier est égal à la moitié, soit 10 cubes. On peut en conclure que pour trouver le nombre de cubes d'un escalier, il suffit de prendre la moitié du nombre de cubes du mur.
Soit h le nombre de cubes de la hauteur de l'escalier, soit C le nombre de cubes de l'escalier :
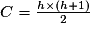 .
.
Soit h le nombre de cubes de la hauteur de l'escalier, soit C le nombre de cubes de l'escalier :
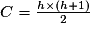 .
.4) Pour 3 523 cubes, appliquons la formule précédente :
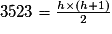
h2 + h = 7 046.
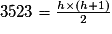
h2 + h = 7 046.
Il suffit alors de résoudre cette équation du second degré : h2 + h − 7 046 = 0.
avec Δ = 1 − (4 × −7 046).
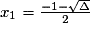 | | 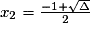 |
avec Δ = 1 − (4 × −7 046).
La première solution donnant un résultat négatif, nous traiterons uniquement la seconde.
Δ = 1 − (4 × −7 046)
Δ = 1 + 28 184
Δ = 28 185
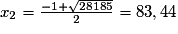 .
.
Δ = 1 − (4 × −7 046)
Δ = 1 + 28 184
Δ = 28 185
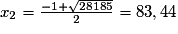 .
.Le nombre de cubes entier le plus proche est 83.
Calculons le nombre de cubes nécessaire pour une hauteur d'escalier de 83 cubes :
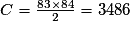 .
.
Nous avions au départ 3 523 cubes, 3 486 sont utilisés.
3 523 − 3 486 = 37
37 < 83.
Il y a 37 cubes non utilisés.
Calculons le nombre de cubes nécessaire pour une hauteur d'escalier de 83 cubes :
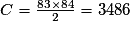 .
.Nous avions au départ 3 523 cubes, 3 486 sont utilisés.
3 523 − 3 486 = 37
37 < 83.
Il y a 37 cubes non utilisés.
Exercice 2 (4 points)
 |
1) L'aire du jardin est la somme de l'aire du rectangle ABED, A1, et de l'aire du triangle BCE, A2.
A1 = 30 × 50
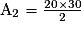
A1 + A2 = 1 500 + 300.
L'aire du jardin est 1 800 m2.
A1 = 30 × 50
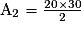
A1 + A2 = 1 500 + 300.
L'aire du jardin est 1 800 m2.
2) L'aire du potager AP est égale à la largeur du terrain (AD) que multiplie x.
AP = 30x.
AP = 30x.
L'aire de la pelouse AH est égale à l'aire totale du terrain amputée de l'aire du potager.
AH = 1 500 − 30x.
AH = 1 500 − 30x.
3) Pour que le potager et la pelouse aient la même aire, on peut procéder de deux manières.
• On a exprimé en fonction de x les deux aires, il nous reste à chercher la valeur de x pour laquelle ces expressions sont égales :
30x = 1 800 − 30x
60x = 1 800
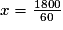
x = 30.
30x = 1 800 − 30x
60x = 1 800
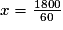
x = 30.
• Si les deux aires ont la même valeur, c'est qu'elles correspondent à la moitié de l'aire totale du terrain, soit 900 m2.
Il suffit alors de trouver pour quelle valeur de x on a 30x = 900 (ou 1 800 − 30x = 900).
30x = 900
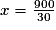
x = 30.
Il suffit alors de trouver pour quelle valeur de x on a 30x = 900 (ou 1 800 − 30x = 900).
30x = 900
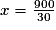
x = 30.
Dans les deux cas, nous trouvons une valeur de x = 30 m.
Le potager a donc un côté AD de 30 mètres et un côté x de 30 mètres, c'est un carré.
Le potager a donc un côté AD de 30 mètres et un côté x de 30 mètres, c'est un carré.
4) a.
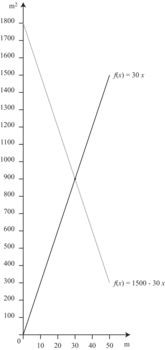 |
b. Les deux courbes se croisent lorsque l'abscisse est égale à 30 (cela correspond à une valeur de x = 30 m) et l'ordonnée à 900 (cela correspond à la moitié de l'aire totale du terrain).
Lorsque x = 30 m, on a bien :
AP = 30 × 30 = 900 m2
et AH = 1800 − 30 × 30 = 900 m2.
Lorsque x = 30 m, on a bien :
AP = 30 × 30 = 900 m2
et AH = 1800 − 30 × 30 = 900 m2.
5) Nous avons une situation de proportionnalité.
Si 10 kg de semences sont nécessaires pour 500 m2,
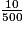 kg de semences sont nécessaires pour 1 m2.
kg de semences sont nécessaires pour 1 m2.
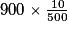 kg de semences sont nécessaires pour 900 m2.
kg de semences sont nécessaires pour 900 m2.
18 kg de semences sont nécessaires pour 900 m2.
Si 10 kg de semences sont nécessaires pour 500 m2,
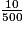 kg de semences sont nécessaires pour 1 m2.
kg de semences sont nécessaires pour 1 m2.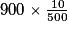 kg de semences sont nécessaires pour 900 m2.
kg de semences sont nécessaires pour 900 m2.18 kg de semences sont nécessaires pour 900 m2.
Question complémentaire (4 points)
Florent cherche à ramener les données des problèmes proposés à la situation de départ, c'est-à-dire qu'il essaie de trouver un rapport avec les 20 euros que veut échanger le personnage de l'image. Il trouve bien 120 = 6 × 20 et 40 = 2 × 20. Ensuite, il applique le facteur trouvé aux francs suisses.
C'est le principe de la proportionnalité « simple », où l'on ne cherche pas de coefficient de proportionnalité, mais où l'on observe les nombres et où l'on applique à tous les mêmes opérations.
Pour 30 euros, la démarche est un peu différente, dans la mesure où l'élève « travaille » sur les données des deux personnages de l'image : il détermine d'abord que 30 = 20 + 10, donc que les 20 premiers euros valent 30 francs suisses ; puis, pour les 10 autres euros, équivalant à la moitié de 20 euros, il fait correspondre la moitié de 30 francs suisses, soit 15 francs suisses. Il fait ensuite la somme. Il s'agit encore de manipuler les données sans appliquer de coefficient de proportionnalité, mais on travaille sur le nombre de départ (les euros) et sur le nombre d'arrivée (les francs suisses) parallèlement. Se profile alors un algorithme prédictif du coefficient : on prend le nombre d'euros auquel on ajoute sa moitié, ce qui correspond à un coefficient de 1,5.
Pour l'exercice 4, l'élève applique sur un plus grand nombre le principe découvert précédemment, et ajoute aux 260, correspondant aux euros de départ, la moitié de 260 pour obtenir le nombre de francs suisses.
Le problème numéro 5 ne correspond plus aux démarches précédentes, même s'il y a volonté de trouver un rapport constant entre les nombres (− 6). Cette dernière question semble avoir dérouté l'élève. La proportionnalité n'est plus le principe retenu. Il la manipulait lorsqu'il construisait lui-même ses réponses, mais il n'y parvient plus lorsqu'il s'agit d'analyser des résultats.
C'est le principe de la proportionnalité « simple », où l'on ne cherche pas de coefficient de proportionnalité, mais où l'on observe les nombres et où l'on applique à tous les mêmes opérations.
Pour 30 euros, la démarche est un peu différente, dans la mesure où l'élève « travaille » sur les données des deux personnages de l'image : il détermine d'abord que 30 = 20 + 10, donc que les 20 premiers euros valent 30 francs suisses ; puis, pour les 10 autres euros, équivalant à la moitié de 20 euros, il fait correspondre la moitié de 30 francs suisses, soit 15 francs suisses. Il fait ensuite la somme. Il s'agit encore de manipuler les données sans appliquer de coefficient de proportionnalité, mais on travaille sur le nombre de départ (les euros) et sur le nombre d'arrivée (les francs suisses) parallèlement. Se profile alors un algorithme prédictif du coefficient : on prend le nombre d'euros auquel on ajoute sa moitié, ce qui correspond à un coefficient de 1,5.
Pour l'exercice 4, l'élève applique sur un plus grand nombre le principe découvert précédemment, et ajoute aux 260, correspondant aux euros de départ, la moitié de 260 pour obtenir le nombre de francs suisses.
Le problème numéro 5 ne correspond plus aux démarches précédentes, même s'il y a volonté de trouver un rapport constant entre les nombres (− 6). Cette dernière question semble avoir dérouté l'élève. La proportionnalité n'est plus le principe retenu. Il la manipulait lorsqu'il construisait lui-même ses réponses, mais il n'y parvient plus lorsqu'il s'agit d'analyser des résultats.
Victor utilise pour tous les problèmes la même démarche : il double le nombre d'euros de départ, puis il retire 10. Ce calcul ne fonctionne que pour l'exemple de départ. Victor a observé, a trouvé des opérations qui conviennent pour ce cas particulier, mais qui ne correspondent pas à une démarche mathématique. Le calcul a été reproduit ensuite. Le principe de coefficient multiplicatif n'est pas assimilé, et c'est l'addition (en l'occurrence la soustraction) qui est utilisée. Peut-être qu'un exemple supplémentaire aurait suffi à induire un autre raisonnement.
Jessy a travaillé par correspondances. Elle a cherché, comme Florent, à se rapprocher des 20 et 30 euros de départ, en appliquant chaque fois les mêmes opérations sur les euros et sur les francs suisses, sauf qu'elle renonce aux opérations proprement dites pour décliner chaque étape (et finir par faire une opération à l'arrivée). Sa méthode est fiable, mais évidemment très longue, ce qui l'empêche peut-être de finir les exercices. Par ailleurs, les trois exercices traités utilisent la même méthode, et c'est sur les deux autres qu'elle aurait dû dévier. C'est peut-être aussi pour cela que les exercices ne sont pas faits. Il n'y a pas à proprement parler d'erreur, mais un manque d'efficacité, qui aurait peut-être conduit à une erreur si les autres exercices avaient été abordés.
Comme Victor, Cécile utilise pour tous les problèmes la même démarche, mais plus simplement que lui. Elle ajoute 10 au nombre d'euros de départ, ce qui est un calcul juste pour l'exemple, mais une démarche fausse (le dernier problème pouvait induire en erreur). Il s'agit d'une interprétation primaire de la situation, où le calcul une fois trouvé est appliqué sans passer par le sens.
Exercice 3 (4 points)
1) Lorsqu'on tire une première étiquette, on a le choix parmi les 10 proposées ; il reste 9 possibilités pour tirer la seconde.
Le nombre de tirages possibles est 10 × 9 = 90.
Le nombre de tirages possibles est 10 × 9 = 90.
Mais dans ce cas, nous aurons des doublons puisque l'association étiquette A-étiquette B est équivalente à l'association étiquette B-étiquette A. Il faut donc diviser par deux le nombre de solutions.
Le nombres de tirages différents est donc 45.
Le nombres de tirages différents est donc 45.
2) a. « Deux angles droits seulement » :
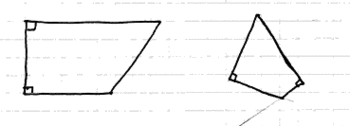 |
b. Les quadrilatères particuliers ayant des diagonales perpendiculaires se limitent à deux sortes : le carré, qui possède 4 angles droits, le losange qui ne possède aucun angle droit. Par ailleurs, si on trace des diagonales perpendiculaires et que l'on réunit aléatoirement leurs extrémités, on obtient un quadrilatère sans angle droit intentionnel. Une figure qui répond à la consigne « deux angles droits seulement » et « diagonales perpendiculaires » est le cerf-volant, appelé aussi deltoïde, dont les deux définitions sont : « quadrilatère convexe ayant deux couples de côtés consécutifs de même longueur » (ce qui n'est pas très intéressant, sauf pour la construction) et « quadrilatère convexe dont une diagonale est la médiatrice de l'autre ».
Programme de construction
- tracer deux segments isométriques consécutifs formant un angle quelconque, AB et AC ;
- avec l'équerre, tracer deux segments issus de B et C formant un angle droit en B et en C ;
- marquer le point D, à l'endroit où se coupent les segments tracés ;
- vérifier que les diagonales sont bien perpendiculaires.
 |
3) Prenons les étiquettes les unes après les autres et vérifions leur compatibilité avec « deux côtés parallèles seulement ».
• « Deux angles droits seulement » : c'est possible, il s'agit du trapèze rectangle dessiné à main levée lors de la question 2.
 |
• « Côtés égaux deux à deux » : ce n'est pas compatible avec « deux côtés parallèles seulement ». En effet, il ne peut s'agir que d'un parallélogramme. Par conséquent, les côtés sont parallèles deux à deux.
• « Quatre côtés égaux » : il s'agit de la même configuration que ci-dessus, encore plus restrictive, car les figures ne peuvent être qu'un carré ou un losange.
• « Diagonales perpendiculaires » : traçons d'abord deux droites d1 et d2 parallèles, puis relions un point quelconque de d1 et un point quelconque de d2. Nous obtenons un segment AC. Cherchons un segment BC perpendiculaire à AC coupant d1 et d2. Relions les 4 points A, B, C et D.
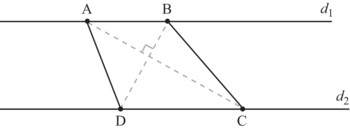 |
• « Quatre angles droits » : il s'agit d'un carré ou d'un rectangle, incompatibles avec « deux côtés parallèles seulement ».
• « Deux côtés égaux seulement » : on peut construire un trapèze isocèle, les côtés parallèles seront alors de mesures différentes, mais les autres côtés seront isométriques.
 |
• « Côtés opposés parallèles » : c'est la définition du parallélogramme, incompatible avec « deux côtés parallèles seulement ».
• « Diagonales égales » : un trapèze isocèle peut correspondre à cette demande conjointe de diagonales égales et deux côtés parallèles seulement.
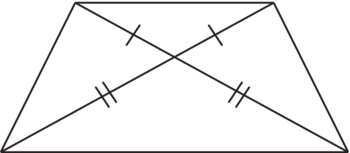 |
• « Diagonales se rencontrant en leur milieu» : c'est un des principes du parallélogramme, incompatible avec « deux côtés parallèles seulement ».
4) Selon la question précédente, le quadrilatère ABCD ne peut être qu'un carré.
Puisque AB = DC, AE = DG et EG = AD.
Puisque AD = BC, BF = AH et HF = AB.
Les diagonales du quadrilatère EFGH sont isométriques puisque AD = AB.
Elles se coupent à angle droit puisque EG est parallèle à AD, HF est parallèle à AB et AB et AD sont perpendiculaires.
Puisque AB = DC, AE = DG et EG = AD.
Puisque AD = BC, BF = AH et HF = AB.
Les diagonales du quadrilatère EFGH sont isométriques puisque AD = AB.
Elles se coupent à angle droit puisque EG est parallèle à AD, HF est parallèle à AB et AB et AD sont perpendiculaires.
On peut aussi considérer les triangles AEH, EBF, FGC, HGD, et selon les remarques précédentes, considérer que leurs hypoténuses sont isométriques, donc que les côtés de cette figure EFGH sont égaux.
Question complémentaire (4 points)
a. Cette activité peut être proposée au cycle 3, plutôt à partir du CM1, les élèves devant être capables, à l'issue de ce cycle, de « reconnaître de manière perceptive une figure plane, [d']en donner le nom, [de] vérifier son existence en ayant recours aux propriétés et aux instruments » et « [d']utiliser à bon escient le vocabulaire suivant : triangle, triangle rectangle, triangle isocèle, triangle équilatéral, carré, rectangle, losange, cercle, sommet, côté, centre, rayon et diamètre ».
L'activité va même au-delà des compétences requises, les propriétés des diagonales étant laissées à l'appréciation de l'enseignant : « Des propriétés relatives aux diagonales des quadrilatères particuliers peuvent être découvertes lors de la résolution de problèmes, mais aucune exigence de compétence ne saurait en découler » (document d'application des programmes mathématiques cycle 3, CNDP, juillet 2002).
On se trouve bien dans un cas de résolution de problème. Les compétences des élèves de cours moyen permettent sinon de le résoudre par une solution experte, au moins de donner des solutions personnelles pour y répondre.
L'activité va même au-delà des compétences requises, les propriétés des diagonales étant laissées à l'appréciation de l'enseignant : « Des propriétés relatives aux diagonales des quadrilatères particuliers peuvent être découvertes lors de la résolution de problèmes, mais aucune exigence de compétence ne saurait en découler » (document d'application des programmes mathématiques cycle 3, CNDP, juillet 2002).
On se trouve bien dans un cas de résolution de problème. Les compétences des élèves de cours moyen permettent sinon de le résoudre par une solution experte, au moins de donner des solutions personnelles pour y répondre.
b. L'objectif de l'exercice consiste à faire chercher la figure réunissant les conditions écrites sur les deux étiquettes pour voir si ces dernières sont compatibles ou non.
Les élèves pourront travailler alors en mobilisant leurs connaissances sur les caractéristiques des parallélogrammes en particulier, des quadrilatères spécifiques (trapèzes) en général.
Les élèves pourront, par tâtonnements, essayer à main levée de combiner les propriétés des étiquettes. Les résultats, une fois validés, pourront être institutionnalisés, appris puis réinvestis.
Les élèves pourront travailler alors en mobilisant leurs connaissances sur les caractéristiques des parallélogrammes en particulier, des quadrilatères spécifiques (trapèzes) en général.
Les élèves pourront, par tâtonnements, essayer à main levée de combiner les propriétés des étiquettes. Les résultats, une fois validés, pourront être institutionnalisés, appris puis réinvestis.
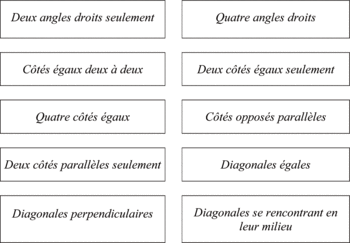
c. L'élève A a procédé en suivant l'une après l'autre les deux consignes. Il a d'abord construit les deux angles droits, puis a tracé deux segments de même longueur, constituant les deux côtés égaux. Pour que ces deux conditions demeurent, le dernier côté doit constituer un rectangle, ce qui bloque à juste titre l'élève.
L'élève B entrevoit la solution du cerf-volant, mais considère que les angles droits demandés sont ceux formés par les diagonales et non ceux des sommets de la figure. Les deux « côtés » égaux, de même, ne sont pas des côtés de la figure, mais ses diagonales. Les deux étiquettes combinées par l'élève seraient plutôt « deux diagonales perpendiculaires » et « deux diagonales égales ».
L'élève C a commencé comme l'élève A, s'est heurté aux mêmes difficultés, et a résolu le problème en ajoutant un sommet et donc un côté, formant une figure qui n'est pas un quadrilatère. En revanche, les deux étiquettes sont respectées. L'élève a privilégié la consigne spécifique au détriment de la consigne générale.
